Scientists Learn the Ropes on Tying Molecular Knots

Through directed self-assembly techniques, chemists are making tiny molecular knots in their labs. The illustration portrays the structure of a five-crossing knot synthesized in 2011.
Olena Shmahalo/Quanta Magazine; Source: David Leigh
Introduction
The world is tied up in knots. They form spontaneously in swirling vortices of smoke, in long strands of yarn or hair, and in the earbud cords that somehow always tangle in one’s pocket. Even down at the molecular scale, they appear in the long chains making up some proteins, and when they arise in DNA’s twists and coils, enzymes have to help unwind them. Biophysicists study these knots to figure out how they get there and how they contribute to the behavior of those molecules.
Chemists, meanwhile, have turned their attention to molecular knots of their own making: smaller synthetic constructions assembled from joined fragments rather than tied in a single continuous biomolecular string. In their labs, they have been painstakingly synthesizing such tiny knots, achieving escalating levels of intricacy, with the hope of eventually exploiting the knots’ unique topologies in new nanotools, pharmaceuticals and novel materials with desirable properties. The most recent — and most complex — knot to join these ranks, a composite structure fashioned out of three simpler knots, was reported last month in Nature Chemistry and took years to build.
In August, other researchers published a theoretical paper in Nature Communications that tabulated which knots chemists should seek to make next. They hope the work will provide insights into what governs the ability of small artificial knots to assemble themselves spontaneously — and help them to get a handle on just how complicated such knots can be.
And despite the significant differences between those designs and the knots found in DNA and proteins, some scientists think that analyzing the synthetic systems could eventually inform the understanding of knotting in biological contexts, too.
Knot Zoos in the Lab
To mathematicians, a knot means something like an ordinary knot tied in string, only the string’s ends are then attached so that the tangle can’t wiggle loose. More formally, it’s a closed curve, embedded in three-dimensional space, that does not intersect itself and cannot be reduced to a simple loop. Knots can be represented as planar projections, two-dimensional drawings with “crossings” where one part of the thread goes over or under another. Two knots are considered the same if one can be shifted and rotated to form the other without altering its fundamental topology.
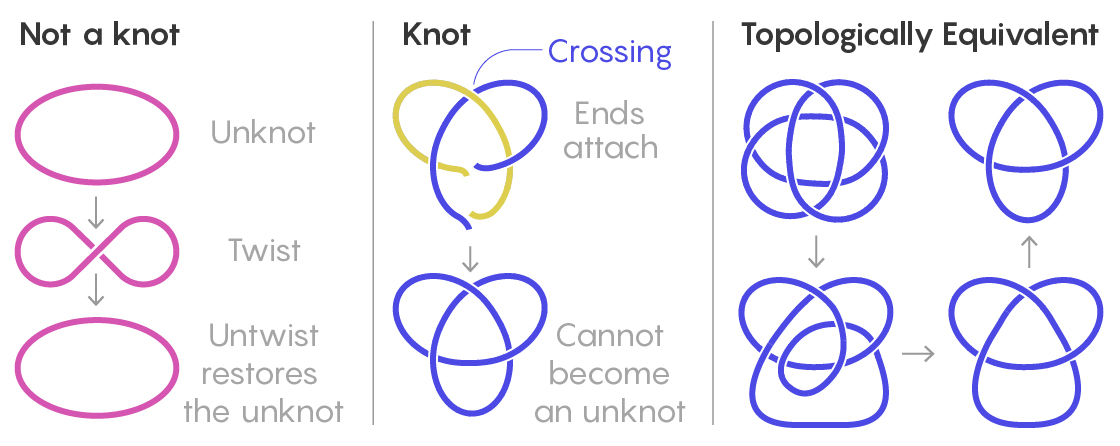
Lucy Reading-Ikkanda/Quanta Magazine
Mathematicians classify knots by ordering them according to their minimum number of crossings. After the “unknot” (a circle) comes the simplest knot, one with three crossings, known as a trefoil. (Knots with one or two crossings are topologically equivalent to the unknot.) Next, there’s one with four crossings, two with five crossings, three with six crossings, seven with seven crossings…. Those numbers then explode: There are 165 knots with 10 crossings, and for 16 crossings, there are more than a million. Moreover, knots can be connected to one another in specific ways to form composite knots.
Chemists want their own creations to attain some of that complexity, but the going has been slow. They manufactured the first molecular knot — the trefoil — in 1989, and for decades, that was it. “That seemed to us an unsatisfactory state of affairs,” said David Leigh, a chemist at the University of Manchester in England. “Just as in the world of fishermen or climbers, [where] different knots have different functions, the same is true in the molecular world.”
Being able to build more complicated knots will, at the least, help researchers to probe how knots affect the strength, flexibility and other features of materials, and to determine which ones are best suited to which purposes. Some experts foresee a future in which knots might be woven together to form functional materials with heat-resistant or catalyzing properties. Others hope to one day use microscopic knots as nests for the safe transport of drug molecules or other minute cargo.
“Creating molecular knots is the best way chemists can show they’ve really mastered the molecular laws,” said Cristian Micheletti, a computational biophysicist at the International School for Advanced Studies in Italy, and the leader of the team that published the Nature Communications paper. “It’s like an intellectual playground” on which researchers can test their mettle.
And so Leigh and others have been making more elaborate kinds of knots, using specially designed fragments and an ionically charged molecular scaffold that can position them for joining. In this way, Leigh most recently succeeded in building the two most complex knots to date: an eight-crossing knot, and a composite, nine-crossing one. He’s currently applying the same strategy to synthesize new configurations.
Ideally, however, scientists would be able to explore such configurations more systematically through an understanding of general knotting patterns and principles of directed self-assembly. That’s what Micheletti and his colleagues set out to make possible.
A New Knot Table
Micheletti’s team wanted to investigate which knots could be synthesized most easily. They used simple computational models to stitch three, four or five identical fragments of a helix together into closed chains, then moved the fragments around without breaking their connections. In this way, the researchers generated thousands of potential configurations. They then identified which kinds of knots had appeared, and picked out those that had a certain degree of symmetry — something common to the handful of molecular knots that chemists have been able to create so far.
That left them with only a small repertoire of knots — knots that in further simulations did indeed self-assemble more frequently. Among them were most of the knots that had been made experimentally to date, as well as new candidates for synthesis that included a 10-crossing and a 15-crossing knot.
Most noteworthy, though, was the discovery that simpler knots are not always easier to make. The next knot to appear after five crossings, for instance, did not contain six crossings but rather eight. The researchers realized that adding crossings sometimes lent a knot symmetry that would make it easier to synthesize. That was the case for one of the eight-crossing knots that the work uncovered: It is topologically equivalent to one with four crossings — but the four-crossing version is more difficult to make.
Working from another way of representing the knots in two dimensions, called braid diagrams (which highlight cyclical aspects of how a thread gets twisted into a knot), Micheletti and his team were able to generalize their findings to larger numbers of building blocks and greater degrees of “interwovenness.” This in turn allowed the researchers to design a new kind of reference table for knots.
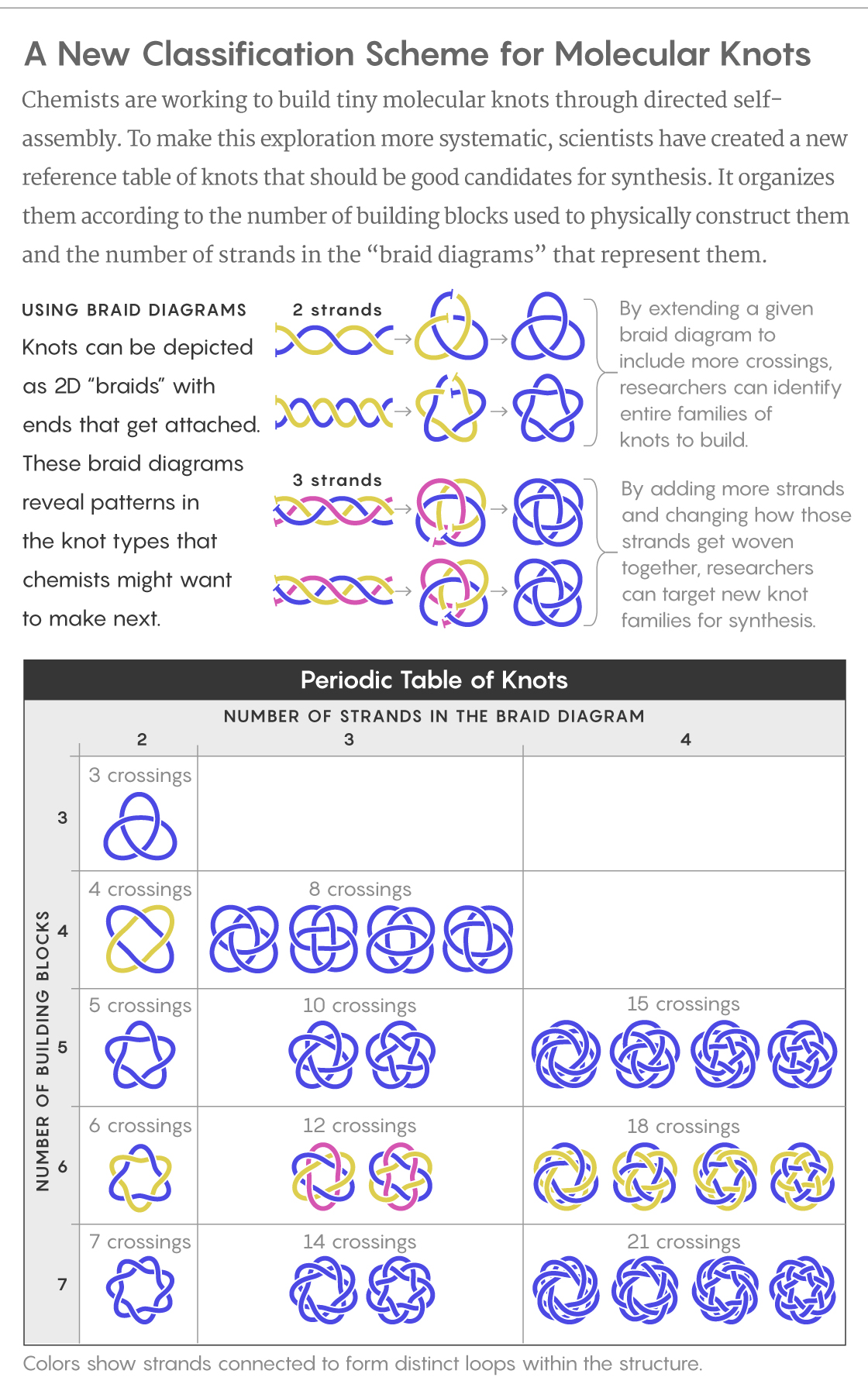
Lucy Reading-Ikkanda/Quanta Magazine; Source: DOI: 10.1038/s41467-018-05413-z
Micheletti acknowledges that his “knot zoo” makes certain assumptions that limit its scope — for example, that the knots will consist only of identical building blocks. Still, his work can start to guide chemists’ further synthesis efforts.
That goes for other theoretical efforts as well. One group, led by Ivan Coluzza, a computational biophysicist who studies protein folding at the Basque Foundation for Science in Spain, is using Micheletti’s work as a reference in tests of how adding new sequences of amino acids to protein-like models affects the fundamental spectrum of knots that arise in them. The work, published earlier this month, has suggested that knotted backbones are so rare in proteins because of the number of amino acid types available for use: With a 20-letter alphabet at their disposal, proteins are less likely to form knots spontaneously than they are when their alphabet consists of only, say, three letters.
A Biological Playground
By continuing to put together a diverse array of knots in the lab, it may be possible to determine how knots self-assemble, and what the knots do to the properties of synthesized strands. And just maybe, some of those insights could one day help biophysicists learn about what knots are doing in DNA, proteins or other molecules in which they naturally emerge. (Some researchers, for instance, suspect that knots confer greater stability to the small number of proteins in which they’re found, but they have yet to prove it.)
It’s important to emphasize that the self-assembly processes Leigh and Micheletti use are quite different from those that produce biomolecules in nature. Experimentally or computationally, Leigh and Micheletti paste together short pieces of material to attain their knots, and the geometry of those pieces constrains what can form. In contrast, biological knots form when a full-length string — of nucleotide bases in DNA, for example, or amino acids in a protein — bends and threads through itself to create any of a massive number of structures.
Nevertheless, Leigh and his colleagues hope that their synthetic work — once it’s reached a sufficient level of complexity — could improve scientists’ understanding of knotting in biology. At the very least, “by identifying these knots that are more likely to occur … it gives us biologists something to look for,” said Lynn Zechiedrich, a molecular biologist who studies the structure and function of DNA at the Baylor College of Medicine. With current imaging technology, after all, it’s been difficult to confirm the structures of very complicated biological knots. Take uncondensed chromosomes, which look like a tangle of spaghetti: They might harbor “these hugely complicated knots [from Micheletti’s table],” Zechiedrich said. “It’s just that we don’t have the resolution to see it.”
“Micheletti’s showing that there are simple ways of creating relatively complex knots. And this might give us a hint that perhaps nature can be using similar ways to create knotted molecules,” added Piotr Szymczak, a theoretical physicist at the University of Warsaw. It could also provide information about whether it’s possible to get more complex topologies in the natural world. Just how intricately shaped can a knot system be and still self-assemble, and does it appear in biomolecules as well?
Leigh, for one, may already be starting to see some hints emerge in his artificial systems (though he cautions that those results have yet to be tested in biological systems). For example, he and his team have observed a correlation between the tightness of knots and how pronounced their chirality, or “handedness,” is (some knots are chiral, meaning that they can never be rotated or shifted to look exactly like their mirror image). Moreover, in 2016, they constructed a five-crossing knot that could speed up chemical reactions. In its unknotted form, the molecule was unable to act as a catalyst, which demonstrates the powerful effects that knots can have in chemistry — and that they may have in biology as well.
Some DNA can supercoil, for instance, the way a coiled telephone cord can twist upon itself. Supercoiling has been an object of research for how it might affect the behavior of DNA — Zechiedrich thinks that in some cases (at least in bacteria), knots and supercoils that don’t get untangled are highly susceptible to mutations — yet chemists haven’t been able to make knots with that supercoiled property to study it in more detail.
But that may change. Leigh’s nine-crossing knot shares some key characteristics with supercoiled DNA. “So by studying these [composite knots] and understanding them in the simple control systems we make, we may be able to develop some insights into what’s happening at the molecular level with supercoiled DNA structures,” Leigh said.
Not everyone agrees. Micheletti himself is skeptical about extrapolating from the synthetic knots to biological ones. Sophie Jackson, a chemist at the University of Cambridge in England who studies knotted proteins, also thinks that the fact that the synthetic knots are made by such a different process means they can’t tell us much about those in DNA and other biomolecules. But “it’s still early days,” Leigh said. “We’ve made only a few different sorts of knots, and have seen only a few different sorts of properties.”
“I think it’s always interesting,” Zechiedrich added, “to push the boundaries and see what else is out there.”
Correction added Oct. 30: In an earlier version of the drawing of topologically equivalent knots, one of the crossings was shown incorrectly.



