Evolutionary Math and Just-So Stories

Dan Page for Quanta Magazine
Introduction
The story of Darwin’s finches — the species of birds that Charles Darwin discovered with marked differences in many surface traits, each adapted to specific islands in the Galápagos — is well known. Based on their fundamental anatomical similarities, Darwin determined that the birds were all related and probably descended from a single ancestral species. That evolution can be vastly accelerated on islands belonging to a single archipelago is now well established. In part, this is because of the small size of such islands and the isolation that they provide to an evolving species. In a recent Quanta article, “Mathematics Shows How to Ensure Evolution,” John Rennie described a mathematical study led by Martin Nowak, who directs an evolutionary dynamics lab at Harvard University, and Krishnendu Chatterjee, a computer scientist at the Institute of Science and Technology Austria. Their mathematical research shows how certain population structures can accelerate or slow down natural selection.
As Rennie explained, the population structures imposed by a group of islands can act as an accelerator of evolution.
Picture a huge population of organisms all living together on one island, for example. A mutation might get permanently lost in the crowd unless its advantage is great. Yet if a few individuals regularly migrate to their own islands to breed, then a modestly helpful mutation might have a better chance of establishing a foothold and spreading back to the main population.
Our first problem provides an intuitive feel for how this could happen.
Problem 1
The probability (p) that an advantageous mutation will get “fixed” (spread through an entire large population of hundreds or thousands of individuals) is 1 − 1/r where r is the relative fitness conferred by the mutation. Thus, a mutation that increases fitness by 5 percent (r = 1.05) has only a 4.7 percent chance of fixation in a large population. By contrast, a mutation that confers a tenfold fitness advantage is almost certain to fix (p = 0.9), while one that has a twofold fitness advantage has an even chance of fixation (p = 0.5). However, even for the mutation that has only a small fitness advantage of 5 percent, the probability of fixation is much larger if the total population is small. Thus in a population of just nine individuals, the fixation probability of the above mutation rises to about 13 percent.
Now imagine that there is an archipelago with a large island that can support a population of thousands of individuals of a species. The archipelago also contains several tiny satellite islands or glorified rocks that can support just nine individuals each. The individuals on these islands cannot leave their rocky home under normal circumstances, but once in a hundred years, there arises a storm powerful enough to blow an individual from the satellite to the main island. If a mutation with a 5 percent fitness advantage has achieved fixation in one of the tiny islands, how long would it take for there to be an even chance that the mutation would achieve fixation on the large island? (Assume that the interval between two storms is long enough for the mutation to either fix or die out on the main island.)
The study described in Rennie’s article shows that this “archipelago paradigm” can theoretically be achieved in any population, even one without any islands, if certain kinds of connections are present in the population. The study uses a simplified model of evolution, as described in the diagrams below.
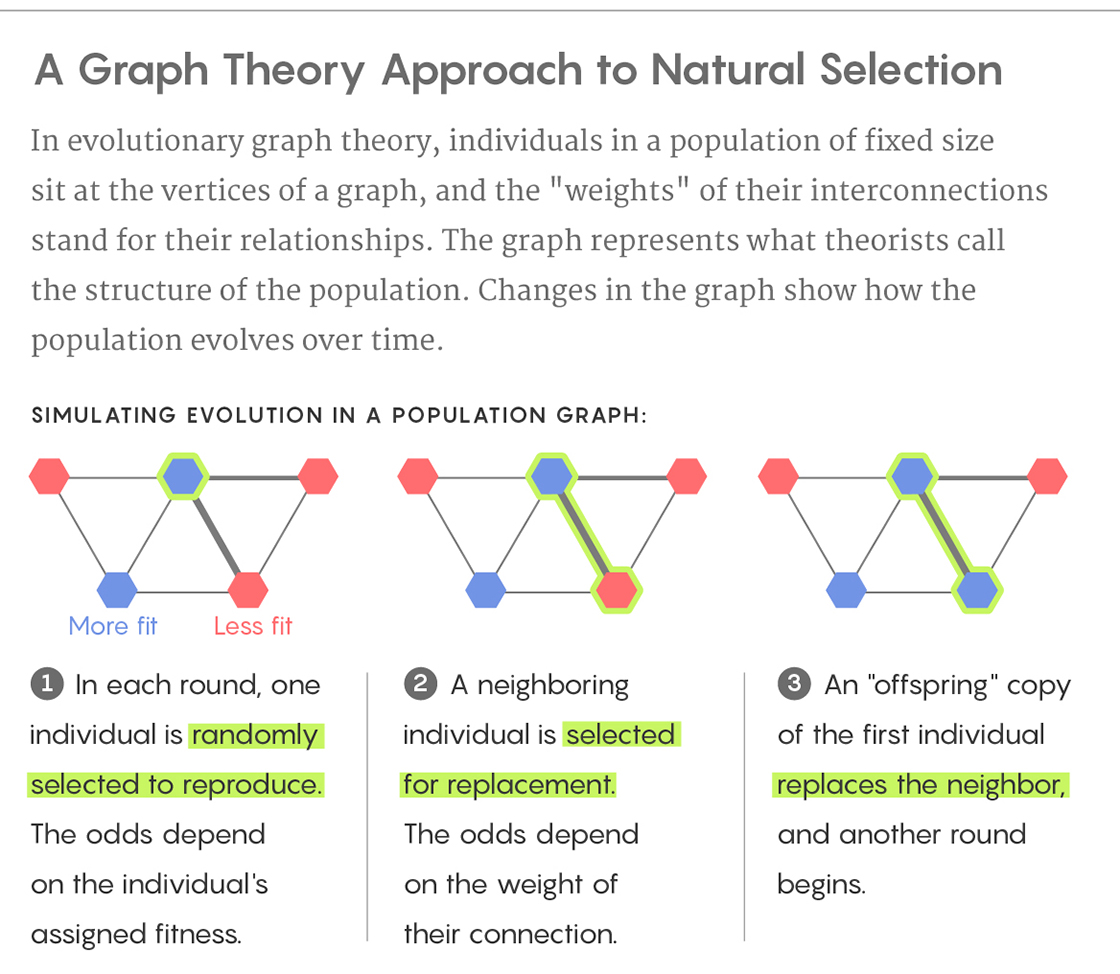
Lucy Reading-Ikkanda/Quanta Magazine
Problem 2
Our second problem examines how the above-described process could progress in a simple grid of nine individuals. Below are three different population structures that could exist among the nine individuals.
Lucy Reading-Ikkanda/Quanta Magazine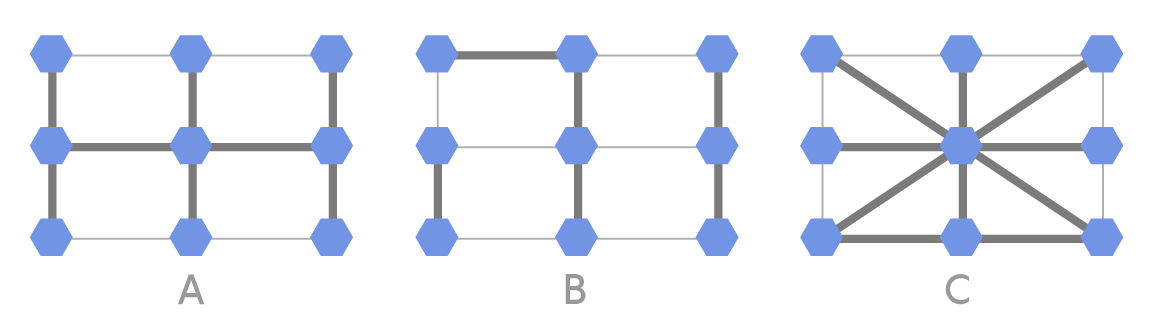
In each of the above population structures, the thicker lines represent strong connections and the thinner lines represent weak connections. One of the nine individuals is initially selected at random to acquire a mutation that gives it a fitness that is 5 percent greater than the others. In each round, one individual is randomly selected to reproduce with a probability proportional to its fitness. Next, one of its neighbors is replaced by an offspring copy of the selected individual. A thick connection indicates a high probability of the neighbor being selected, while a thin connection indicates a low probability. In this process, a normal individual could be replaced by a mutated individual or vice versa. This process continues until the mutation either disappears or all nine individuals are mutated (fixation). For each of the three population structures A, B and C, can you predict if fixation will happen more easily, normally or less easily? Why? What would happen if the thick and thin lines in the configurations were swapped?
Readers who enjoy programming can set up a simulation to see whether the intuitive expectations pan out. Assume that a neighbor with a thick connection to the selected individual has five times the probability of replacement as one with a thin connection. Recall that the fixation probability for a mutation with a 5 percent fitness advantage in a population of nine is about 13 percent. Is the value for any of the configurations significantly greater or less than that?
How relevant are the conclusions of such mathematical reasoning to evolution in the real world? After all, there are several assumptions in this model that are much too simplistic or even downright unrealistic. Reproduction does not surgically erase and replace one particular chosen animal connected to the reproducing individual. Rather, every act of reproduction uses some of the finite resources available to the population, thus putting incremental pressure on all its members, eventually likely affecting the weakest or unhealthiest members. Reproduction and replacement occur in parallel all over the population, not serially and locally. Furthermore, as the authors acknowledge, the model applies to asexual reproduction only: Sexual reproduction makes things far more complex.
The famous American paleontologist and popular science writer Stephen Jay Gould issued a stern warning against seductively simple but unsubstantiated explanations for the evolution of traits, pejoratively calling them “just-so stories” after the title of Rudyard Kipling’s book of children’s tales that had fanciful accounts of such things as “How the Camel Got His Hump.” Such warnings have been stridently applied by several authors to evolutionary psychology as well as to the current problem of the origin of “advantageous” traits, sometimes with trenchant humor.
The problem is that it is easy to create evolutionary stories and tweak the parameters of mathematical models so that they can be used to plausibly argue or explain a certain conclusion — and its opposite. This statement is a case in point: “If men preferred older women, that could be ‘explained’ by pointing out that older women are ‘proven’ as mothers.”
Mathematical models can certainly provide deep insights into evolution. In previous Insights puzzles we’ve touched on a few famous ones that have done so, such as Ronald Fisher’s assertion that tiny mutations have a 50 percent chance of being beneficial, not to mention the Hardy-Weinberg equilibrium. Another hugely successful and now widely accepted mathematical model is Motoo Kimura’s neutral theory of molecular evolution. But it must be remembered that while qualitative and mathematical arguments are relatively easy to construct and can show that certain things could have happened in nature, evolutionary biology is essentially a historical science in which the crucial question is: Did it actually happen in the manner described?
This is extraordinarily difficult to prove. Substantiating evolutionary arguments — whether mathematical or otherwise — requires painstaking field work of the kind done by Darwin himself. One recent example of dedicated field biology is that of the husband and wife team of Rosemary and Peter Grant, who spent several months each year over 40 years on a tiny island in the Galápagos, industriously tagging over 20,000 birds, in order to see evolution in action among Darwin’s finches.
Having just warned you against believing evolutionary just-so stories, let me tell you about one that I find endlessly fascinating: It’s called the grandmother hypothesis and states that grandmothering helped humans — and whales — to live longer. The hypothesis is that in gathering food for their offsprings’ children, older women freed up their daughters to have more children more quickly. So the longest living grandmothers had the most grandchildren, to whom they passed on their longevity-promoting genes. The point in time at which the drain on household resources to care for infirm grandparents exceeded the benefit of the care for new offspring provided by grandparents got pushed back later and later and a negative connection was changed into a positive one. But the kind of replacement selection described in the graph theory model is alive and well, even in the modern world. Jacob Bronowski has graphically described what happens at that critical point in a race of modern nomads even today: “What happens to the old when they cannot cross the last river? Nothing. They stay behind to die. Only the dog is puzzled to see a man abandoned. The man accepts the nomad custom; he has come to the end of his journey, and there is no place at the end.”
Here is a somewhat realistic scenario in which the graph theory model discussed above can apply to humans — where the success of one individual (a grandmother) results in the selective advantage and eventual disadvantage to some strongly connected individuals (the grandchildren) but not to others.
Could this hypothesis be true? There is some empirical evidence for it in the form of studies of aging carried out on fossil teeth that indicate a steady lengthening of lifespan becoming noticeable about 30,000 years ago, and in the fact that among whales who are also long-lived, older females also help in child-rearing into old age. However, the mathematical models are all over the map, ranging from one study that concludes that this factor had almost no effect on longevity, to another that says that it could cause doubling of the lifespan in as little as 60,000 years.
I invite readers to contribute their insights on this hypothesis. As for me, I can feel my heart rooting for Nana! It had to have been just so.
Editor’s note: The reader who submits the most interesting, creative or insightful solution (as judged by the columnist) in the comments section will receive a Quanta Magazine T-shirt. And if you’d like to suggest a favorite puzzle for a future Insights column, submit it as a comment below, clearly marked “NEW PUZZLE SUGGESTION.” (It will not appear online, so solutions to the puzzle above should be submitted separately.)
Note that we may hold comments for the first day or two to allow for independent contributions by readers.
Update: The solution has been published here.



