The Grand Unified Theory of Rogue Waves

Rogue waves long lived only as sailor lore. Hard evidence of their existence has come only in the past few decades.
Andreas Rocha for Quanta Magazine
Introduction
Two weeks before Christmas in 1978, the cargo ship MS München encountered a fierce storm in the North Atlantic. Although the captain couldn’t evade it, the forecasted waves and winds should have posed no threat to the 261-meter-long ship. At midnight, just three hours earlier, an operator had radioed out to a cruise ship, “Have a good trip and see you soon.” Now came a distress call from the München — then silence. The West German vessel and its 28-person crew vanished, leaving behind just four lifeboats, three shipping containers, and a handful of flotation devices.
One clue in particular stumped investigators. A recovered lifeboat — originally bolted to the München about 20 meters above the water — appeared to have been ripped from its perch by a tremendous force hurtling toward the ship’s stern. Rumors circulated that a monstrous wave had crashed onto the deck from above, but such a swell was, at the time, unthinkable. West Germany’s Maritime Board of Inquiry eventually declared it “impossible to explain the cause of the sinking.”
Mariners have known for centuries what researchers have documented only in recent decades: The ocean is a far more dangerous place than common sense would suggest. Data-driven researchers long struggled to square sailors’ tales of monstrous “rogue” waves with the expectation that wave heights vary like human heights — clustering around an average with a few outliers dotting the thin tails of a bell curve. Sure, you might get a wave twice as tall as its neighbors in theory, but you’d have to watch the seas for a long time.
That skepticism changed on New Year’s Day in 1995, when a rogue wave struck the Draupner oil installation in the Norwegian North Sea. Equipped with a downward-pointing laser, the platform recorded a 26-meter wave spiking out of a sea filled with 11.8-meter waves — a nautical Bigfoot caught in a high-resolution snapshot. This hard evidence turned maritime myth into fact. Researchers have since determined that rogue waves probably claimed 22 supercarriers and more than 500 lives in the second half of the 20th century alone.
The Draupner wave spurred physicists to understand exactly how these solitary behemoths might arise. Researchers have since come up with two main theories. Each can describe how large waves form in laboratory wave pools. But debate rages as to which matters more in the ocean.
Now, a group of applied mathematicians reports that they’ve found a way to sidestep the fight over the specific mechanism and focus on predicting the outcome — paving the way for machinery that could, for instance, scan the ocean and notify ship captains that they face a 13% chance of running into a 30-meter wave in the next 15 minutes. The work implies that “impossible” waves of all flavors may share a unified fundamental character.
“You could imagine that a rogue wave of 30 meters in the ocean could happen in many different ways,” said Eric Vanden-Eijnden, an applied mathematician at New York University’s Courant Institute of Mathematical Sciences who helped develop the statistical framework. “But the answer is no.”
Wave Addition
In Draupner’s wake, two schools of thought surfaced regarding how monstrous waves could develop.
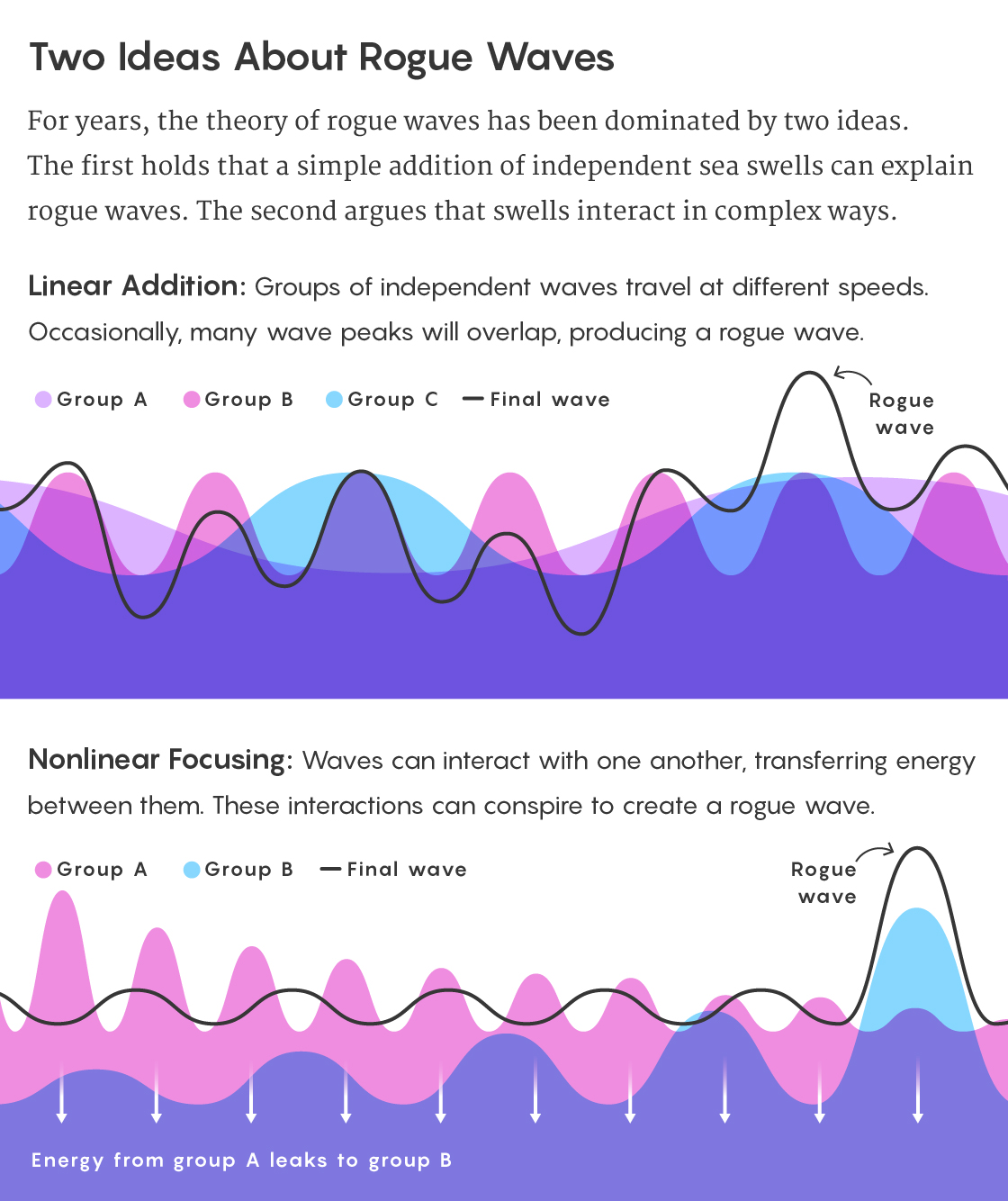
The first is the simplest. It starts with the observation that swells travel at different speeds. When one overtakes another, the two are combined. If a number of swells happen to overlap at the same place at the same time, a rogue wave results, but the component waves always act completely independently of each other. Francesco Fedele, an ocean engineer at the Georgia Institute of Technology, describes this so-called linear addition mechanism as “fortune playing dice with the ocean.”
Oceanographers have long used this approach to calculate the chance that a wave of a given height will arise, but that forecasting method remains controversial, as it seems to underestimate the likelihood of monsters like Draupner.

This rogue wave was spotted in the Atlantic ocean off the coast of North Carolina.
Some researchers, like Fedele, think the traditional method can be salvaged. In 2016 research, he and his colleagues concluded that modifying wave equations to include pointed crests and rounded troughs — as opposed to treating them all as smooth sinusoidal curves — is enough to explain all ocean waves.
Others, however, hold that the most extreme waves form from less straightforward behavior. In wave tanks, for instance, when one wave travels right next to another of similar length, energy leaks from one to the other. The individual swells affect one another in complicated nonlinear ways, as captured in the nonlinear Schrödinger equation, oceanography’s bread-and-butter wave model. (Its apparent connection to quantum theory is not incidental — subatomic particles, after all, behave like waves.) The equation is impossible to solve perfectly in most cases, but numerical explorations have revealed that when the conditions are right, waves actively gather of their own accord. “They have the tendency to conspire to create something big,” Vanden-Eijnden said.
But could this effect, known as nonlinear focusing, have sunk the München? Linear-wave supporters such as Fedele say no. Waves in tanks are confined, they argue, but waves in the open ocean spread out before they can congregate. Other researchers say we don’t yet know the real ocean well enough. Certain winds may mimic the conditions in wave tanks, they say, creating rogue wave breeding grounds.
Lucy Reading-Ikkanda/Quanta Magazine
In the real world, both mechanisms could be relevant. “We came to the conclusion, after evaluating hundreds of papers, that the dominant mechanism at play depends on the situation,” said Amin Chabchoub, a wave physicist at the University of Sydney who co-authored a review of the debate last fall. Linear addition explains some rogue waves, but it underestimates their likelihood in special circumstances, where nonlinear approaches appear to work better. In some cases, both mechanisms may conspire to push waves to impossible heights.
Now researchers may not have to figure out which mechanism is responsible. Vanden-Eijnden and his colleagues have developed a one-size-fits-all statistical framework, which they published in December in Physical Review X. It predicts the probability of encountering any rogue wave, regardless of how it came to be. “There’s no restriction to a linear model, or to a nonlinear propagation model,” or to any model you can imagine, said Ton van den Bremer, a fluid dynamicist at the University of Oxford who was not involved in the research. It could be “a man riding on a donkey. It doesn’t matter.”
The Universal Wave
The trick to describing rogue waves universally, Vanden-Eijnden explained, is to understand that extremely rare events have a logic all their own. Consider gambling. A casino would be wise to carry enough cash to cover a situation where one player won three straight roulette bets using a lucky number, since a three-spin hot streak is likely to happen every 50,000 visits. But it can safely ignore the possibility of 10 straight wins, which would require, on average, 100 trillion spins. When it comes to uncommon events, you can estimate odds quite accurately by focusing on the least rare event, rather than exhaustively tallying up every possible outcome.
Standard arithmetic suffices for simple casino games, but this thinking captures the spirit of a branch of probability known as large deviation theory (LDT). It specializes in identifying instances of rare events that are much more common than the next most likely way they might play out. In the exceptional cases when LDT can be used, it allows calculations that are impossible with standard statistics, Vanden-Eijnden said, just as calculus can solve problems that are intractable in algebra.
The chaotic ocean, the group reasoned, should be the perfect arena to witness LDT in action. A small wave might arise in any number of ways, but rogue waves, by definition, are special. If you witness one, you know that everything went perfectly to create that wave — it’s the nautical equivalent of hitting your number three times in a row. Other evolutions might be theoretically conceivable (like a 10-spin hot streak) but improbable in practice. To forecast the chance of an ordinary wave developing into an extreme outlier, you need to find the one special — but not impossible — path where nothing will get in its way.
The mathematicians first tested their framework, an application of LDT to the nonlinear Schrödinger equation (NLSE), on digitally generated waves in 2018. They asked the computer for random sets of waves satisfying certain “sea states,” each with a characteristic range of heights and wavelengths. They then used the NLSE to peek into the future of each sea, and they used LDT to focus on which would be most likely to generate a wave that would hit an extreme height. As they hoped, they found that for a given type of digital sea, only one specific pattern of initial ripples tended to grow into a rogue wave.


On January 1, 1995, the Draupner oil platform in the North Sea recorded a 26-meter-high rogue wave. Researchers have attempted to recreate the Draupner wave in miniature (top) in order to understand the conditions that led to its formation. The research was done at the Flowave Ocean Research Energy Facility at the University of Edinburgh, which consists of a 25-meter diameter pool surrounded by 168 wave makers.
On January 1, 1995, the Draupner oil platform in the North Sea recorded a 26-meter-high rogue wave. Researchers have attempted to recreate the Draupner wave in miniature (left) in order to understand the conditions that led to its formation. The research was done at the Flowave Ocean Research Energy Facility at the University of Edinburgh, which consists of a 25-meter diameter pool surrounded by 168 wave makers (right).
Mark McAllister, DOI: https://doi.org/10.1017/jfm.2018.886; School of Engineering, University of Edinburgh
Next came physical waves. The mathematicians approached Miguel Onorato, a wave physicist at the University of Turin in Italy. He had spent the early 2000s recreating rogue waves in one of Europe’s largest wave experiments — a nearly 270-meter-long flume in Norway — where he showed that some outliers developed linearly, some nonlinearly, and some in both ways.
Onorato’s data set spanned a variety of seas (albeit artificial and one-dimensional ones), each randomly generated by a wave maker. For each trial, the group knew only high-level statistical properties, such as the typical wave height — imperfect information you could imagine gathering from weather stations or ship-mounted sensors.
But those rough statistics were enough. Large deviation theory boils down to an optimization problem that predicts the archetypal path — unfolding like a movie from the first ripples to the final peak — an aspiring rogue wave has to follow to reach a certain height. And it worked. The highest laboratory waves closely traced out the framework’s prediction, the researchers found, supporting their assumption that the most dangerous waves have almost no flexibility in how they develop. “If the events happen, they happen along the same trajectory,” said Tobias Grafke, a mathematician at the University of Warwick in the UK and a co-author of the work.
If miniature sailors in a toy boat had been sailing in Onorato’s wave tank, they would have been wise to heed the team’s forecasts. The vast majority of seas did not produce any waves high enough to be considered rogue. But 300 or so did, and on average, each type of rogue wave developed as LDT predicted — even with no assumptions as to whether it formed linearly, nonlinearly, or from a mixture of both.
The framework also let the group take a description of an initial sea state and use it to predict whether an extreme wave would develop. Such a prediction would be simple for a godlike figure who knew the perfect position of every initial ripple, but neither linear nor nonlinear theory has been able to make good predictions from a rough description of a general sea state. This one was. “To me, the startling finding here,” said Agis Athanassoulis, a mathematician at the University of Dundee in Scotland, is that “there are going to be specific kinds of initial conditions that generate these events.”
And that ability to estimate the worst-case scenario is exactly what ocean engineers need to know. Insurers require companies to test ships and oil platforms in wave basins. But time in the tanks is pricey, and the new framework could cut down on lengthy brute-force tests. “We don’t want to run a 24-hour slot of random waves. Ideally, we want to run one representative [every-10,000-year] event,” van den Bremer said. “This is quite an important way of beginning to actually do that.”
Others find it less novel. Fedele says that it represents a rediscovery of results he published in 2007, in which he extended a statistical approach developed by the oceanographer Paolo Boccotti. The authors of the recent research believe their work more fully encompasses nonlinear behavior.
The framework has its limits: It can’t capture effects like currents and winds, and it allows waves to grow to any height. These are consequences of its reliance on the nonlinear Schrödinger equation, which doesn’t include these effects either. “I mean waves break, thank God,” Fedele said. “You don’t want to be in an NLSE ocean.”
The authors say that their tools are portable, and that the NLSE engine can be swapped out for other wave theories with more bells and whistles. “It’s like building a car,” Vanden-Eijnden said. “Once you’ve done it you can build other cars the same way.” The most urgent modification will be to swap out the theoretical guts for a model that allows waves to spread freely in the open ocean, instead of being confined to a wave flume.
As the theoreticians tinker with their tools, Onorato is preparing for the next step — seeking more complete measurements of wild waves. Buoys and lasers measure the rise and fall of just one spot in a large field, making it hard to distinguish between linear and nonlinear formation. “We don’t have the full history,” he said. “We don’t know 1 kilometer before what the wave was like or what it’s going to be after.”
To capture waves in all their expansive glory, he stuck two stereoscopic cameras to the upper deck of an icebreaker as it sailed across the tempestuous Southern Ocean from Cape Town to Antarctica in 2017. He and two colleagues recorded two weeks of sea conditions, including a cyclone. “Every time we went to go out to look at the camera or clean the screen,” said Alessandro Toffoli, an oceanographer who participated in the voyage, “really there was a fear of being blown away.”
They’re currently analyzing the videos, subtracting the bucking motion of the boat and extracting the shifting ocean surface from 7 terabytes of data. The group has taken only a preliminary look at the water shortly before the cyclone hit, but nonlinear focusing appears to have played a key role in wave formation that day. Onorato has also begun checking if the LDT framework sinks or swims in the Antarctic seas. “It looks very promising,” he said.
Sailors facing an imminent storm don’t have years to study the growing waves around them, but the new framework represents small steps toward the long-term goal for rogue wave prediction — machinery that scans the ocean and sounds the alarm when it’s time to batten down the hatches. LDT tools, once they’re modified for the open ocean, could be one way for those on boats like the München to know the moment a rogue wave starts focusing.
“Before, you had this mythological monster that could be anything and everywhere.” Athanassoulis said. “Now you have this picture, you have these fingerprints, and you know what you’re looking for.”
Editor’s note: Onorato has received funding from the Simons Foundation, which also funds this editorially independent magazine.





