What Makes the Hardest Equations in Physics So Difficult?

Introduction
Physics contains equations that describe everything from the stretching of space-time to the flitter of photons. Yet only one set of equations is considered so mathematically challenging that it’s been chosen as one of seven “Millennium Prize Problems” endowed by the Clay Mathematics Institute with a $1 million reward: the Navier-Stokes equations, which describe how fluids flow.
Last month I wrote a story about an important new result related to those equations. If anything, the new work suggests that progress on the Millennium Prize will be even harder than expected. Why are these equations, which describe familiar phenomena such as water flowing through a hose, so much harder to understand mathematically than, say, Einstein’s field equations, which involve stupefying objects like black holes?
The answer, I discovered, is turbulence. It’s something we’ve all experienced, whether flying through choppy air at 30,000 feet or watching a whirlpool gather in the bathtub drain. Yet familiarity hasn’t bred knowledge: Turbulence is one of the least understood parts of the physical world.
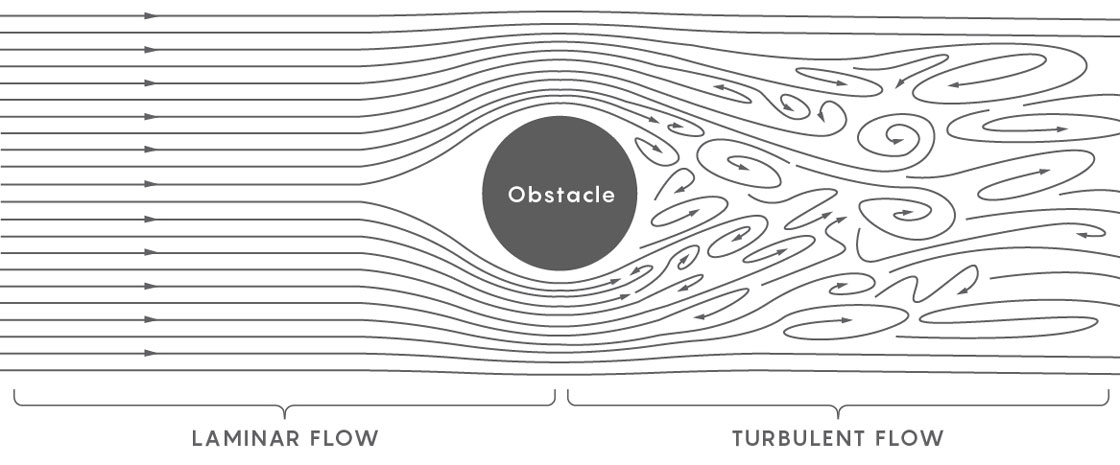
Lucy Reading-Ikkanda/Quanta Magazine
An example of a nonturbulent flow is a smooth river: Every part of the river moves in the same direction at the same speed. A turbulent fluid is the fracturing of that river, so that different parts of the flow move in different directions at different velocities. Physicists describe the formation of turbulence as, first, an eddy in a smooth flow, and then the formation of eddies within that eddy, and yet finer eddies within those eddies — eddies all the way down, so that the fluid becomes broken into discrete parts, all interacting, each moving its own way.
Researchers want to understand exactly how a smooth flow breaks down into a turbulent flow and to model the future shape of a fluid once turbulence has taken over. But the Millennium Prize asks for something much more modest: proving that solutions will always exist. That is, can the equations describe any fluid, from any starting conditions, indefinitely far into the future?
“A first step is simply to try to prove that the equations give rise to some solutions,” said Charlie Fefferman, a mathematician at Princeton University. “That doesn’t give a real understanding of how fluids behave, but if you don’t have that, you don’t know anything.”
So how do you prove that solutions exist? Well, start by thinking about what could make them not exist. The Navier-Stokes equations involve calculating changes in quantities like velocity and pressure. Mathematicians worry about this kind of scenario: You’re running the equations, and after some finite amount of time, they tell you a particle in the fluid is moving infinitely fast. That would be a problem because you can’t calculate the change of an infinite value any more than you can divide by zero. Mathematicians refer to such scenarios as “blowup,” and in a blowup scenario you’d say the equations break down and solutions don’t exist.
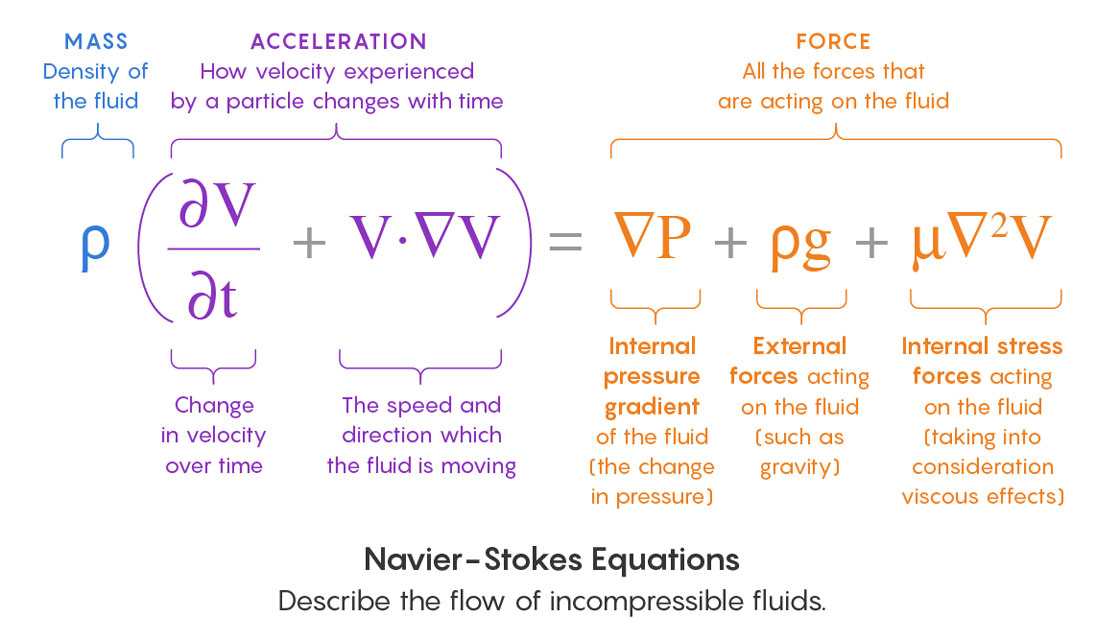
Quanta Magazine
Proving that blowup doesn’t happen (and that solutions always exist) is tantamount to proving that the maximum velocity of any particle within the fluid stays bounded below some finite number. One of the most important of these quantities is the kinetic energy in the fluid.
When you start modeling a flow using Navier-Stokes, your fluid will have some initial amount of energy. But in a turbulent flow, that energy can get concentrated. Instead of being distributed evenly across the river, kinetic energy may gather in arbitrarily small eddies, and particles in those eddies could (theoretically) be accelerated to infinite velocity.
“As I go to smaller and smaller scales, the kinetic energy becomes less and less useful for controlling the solution. My solution can do whatever it wants, and I won’t know how to control it,” said Vlad Vicol, a mathematician at Princeton University and coauthor with Tristan Buckmaster of the new work.
Mathematicians classify partial differential equations like Navier-Stokes based on the extent to which they can go haywire at infinitesimally small scales. Navier-Stokes is on the extreme end of the spectrum. The difficulty of the mathematics of the equation is, in some sense, an exact reflection of the complexity of the turbulent flows they’re supposed to be able to describe.
“When you zoom in on a point, from a mathematical point of view you lose information about the solution,” said Vicol. “But turbulence is meant to describe exactly this — the transfer of kinetic energy from large to smaller and smaller scales, so it’s exactly asking you to zoom in.”

Created with Wind Tunnel.
Whenever you’re talking about the mathematics of equations from physics, it’s natural to wonder: Will any of this change the way we think about the physical world? With the Navier-Stokes equations and the Millennium Prize, the answer is both yes and no. After nearly 200 years of experiments, it’s clear the equations work: The flows predicted by Navier-Stokes consistently match flows observed in experiments. If you’re a physicist working in a lab, that correspondence might be enough. But mathematicians want to know more than that — they want to be able to check if one can follow the equations all the way through, to see exactly how a flow changes moment by moment (for any initial configuration of a fluid) and even to pinpoint the onset of turbulence.
“The behavior of fluids provides surprises,” said Fefferman. “The surprises are in principle explained by the fundamental equations that tell fluids how to move, but getting from the equations that tell fluids how to move to any description of how fluids actually move is very mysterious.”