
Elementary particles are the basic stuff of the universe. They are also deeply strange.
Illustrations by Ashley Mackenzie for Quanta Magazine
Introduction
Given that everything in the universe reduces to particles, a question presents itself: What are particles?
The easy answer quickly shows itself to be unsatisfying. Namely, electrons, photons, quarks and other “fundamental” particles supposedly lack substructure or physical extent. “We basically think of a particle as a pointlike object,” said Mary Gaillard, a particle theorist at the University of California, Berkeley who predicted the masses of two types of quarks in the 1970s. And yet particles have distinct traits, such as charge and mass. How can a dimensionless point bear weight?
“We say they are ‘fundamental,’” said Xiao-Gang Wen, a theoretical physicist at the Massachusetts Institute of Technology. “But that’s just a [way to say] to students, ‘Don’t ask! I don’t know the answer. It’s fundamental; don’t ask anymore.’”
With any other object, the object’s properties depend on its physical makeup — ultimately, its constituent particles. But those particles’ properties derive not from constituents of their own but from mathematical patterns. As points of contact between mathematics and reality, particles straddle both worlds with an uncertain footing.
When I recently asked a dozen particle physicists what a particle is, they gave remarkably diverse descriptions. They emphasized that their answers don’t conflict so much as capture different facets of the truth. They also described two major research thrusts in fundamental physics today that are pursuing a more satisfying, all-encompassing picture of particles.
“‘What is a particle?’ indeed is a very interesting question,” said Wen. “Nowadays there is progress in this direction. I should not say there’s a unified point of view, but there’s several different points of view, and all look interesting.”
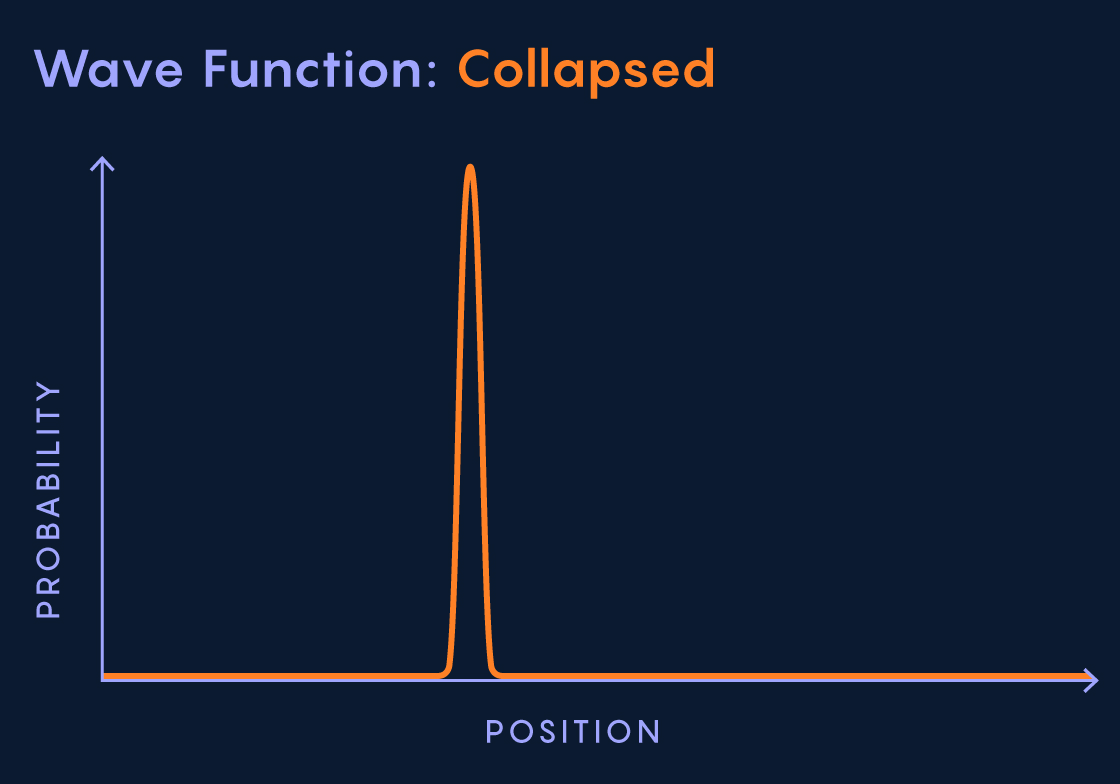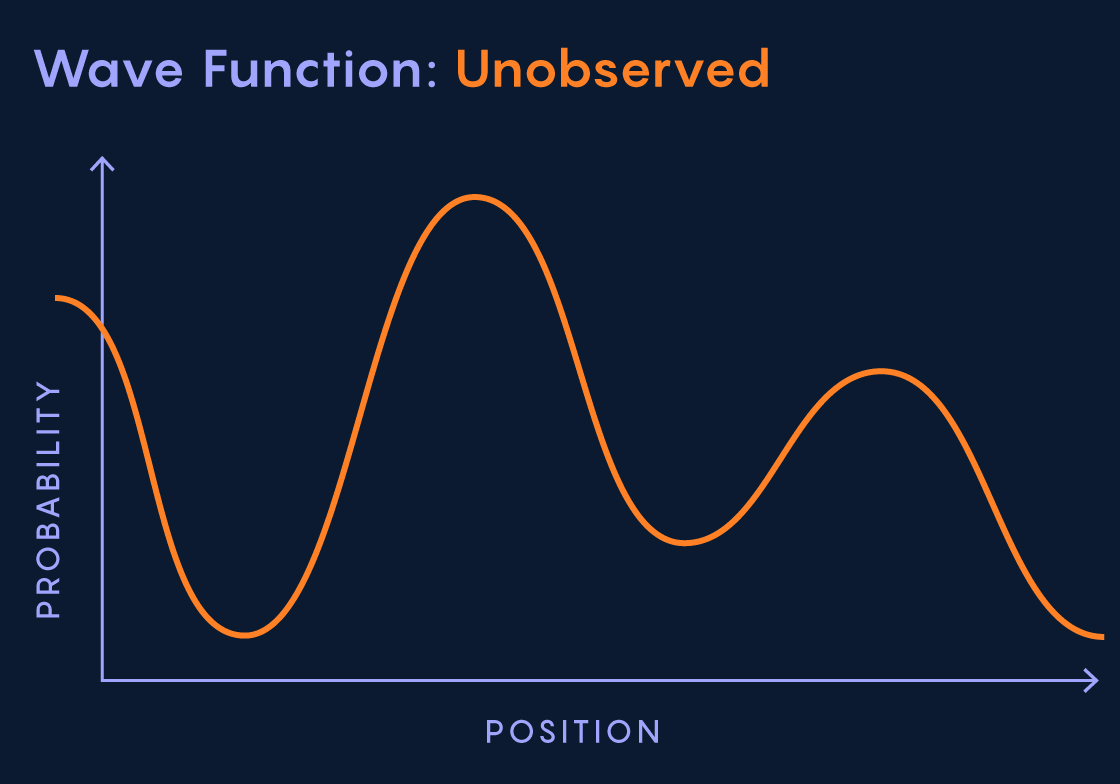
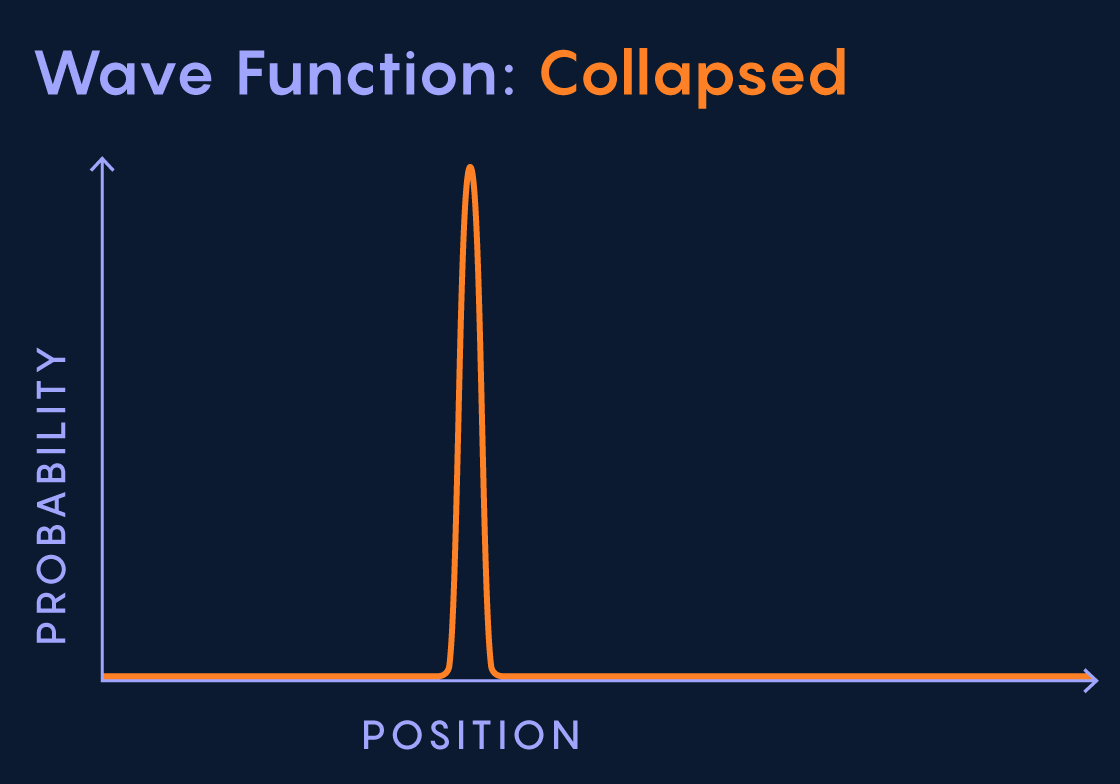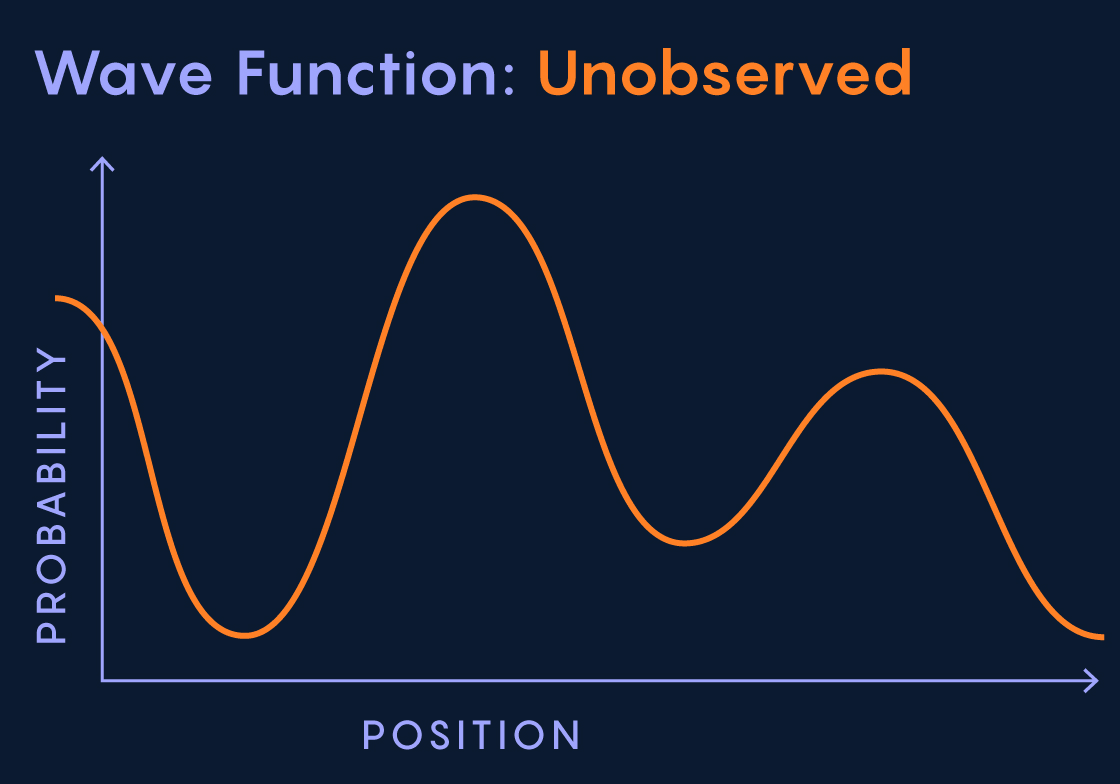
A Particle Is a ‘Collapsed Wave Function’1

The quest to understand nature’s fundamental building blocks began with the ancient Greek philosopher Democritus’s assertion that such things exist. Two millennia later, Isaac Newton and Christiaan Huygens debated whether light is made of particles or waves. The discovery of quantum mechanics some 250 years after that proved both luminaries right: Light comes in individual packets of energy known as photons, which behave as both particles and waves.
Wave-particle duality turned out to be a symptom of a deep strangeness. Quantum mechanics revealed to its discoverers in the 1920s that photons and other quantum objects are best described not as particles or waves but by abstract “wave functions” — evolving mathematical functions that indicate a particle’s probability of having various properties. The wave function representing an electron, say, is spatially spread out, so that the electron has possible locations rather than a definite one. But somehow, strangely, when you stick a detector in the scene and measure the electron’s location, its wave function suddenly “collapses” to a point, and the particle clicks at that position in the detector.
Samuel Velasco/Quanta Magazine
A particle is thus a collapsed wave function. But what in the world does that mean? Why does observation cause a distended mathematical function to collapse and a concrete particle to appear? And what decides the measurement’s outcome? Nearly a century later, physicists have no idea.
A Particle Is a ‘Quantum Excitation of a Field’2

The picture soon got even stranger. In the 1930s, physicists realized that the wave functions of many individual photons collectively behave like a single wave propagating through conjoined electric and magnetic fields — exactly the classical picture of light discovered in the 19th century by James Clerk Maxwell. These researchers found that they could “quantize” classical field theory, restricting fields so that they could only oscillate in discrete amounts known as the “quanta” of the fields. In addition to photons — the quanta of light — Paul Dirac and others discovered that the idea could be extrapolated to electrons and everything else: According to quantum field theory, particles are excitations of quantum fields that fill all of space.
In positing the existence of these more fundamental fields, quantum field theory stripped particles of status, characterizing them as mere bits of energy that set fields sloshing. Yet despite the ontological baggage of omnipresent fields, quantum field theory became the lingua franca of particle physics because it allows researchers to calculate with extreme precision what happens when particles interact — particle interactions being, at base level, the way the world is put together.
As physicists discovered more of nature’s particles and their associated fields, a parallel perspective developed. The properties of these particles and fields appeared to follow numerical patterns. By extending these patterns, physicists were able to predict the existence of more particles. “Once you encode the patterns you observe into the mathematics, the mathematics is predictive; it tells you more things you might observe,” explained Helen Quinn, an emeritus particle physicist at Stanford University.
The patterns also suggested a more abstract and potentially deeper perspective on what particles actually are.
A Particle Is an ‘Irreducible
Representation of a Group’3

Mark Van Raamsdonk remembers the beginning of the first class he took on quantum field theory as a Princeton University graduate student. The professor came in, looked out at the students, and asked, “What is a particle?”
“An irreducible representation of the Poincaré group,” a precocious classmate answered.
Taking the apparently correct definition to be general knowledge, the professor skipped any explanation and launched into an inscrutable series of lectures. “That entire semester I didn’t learn a single thing from the course,” said Van Raamsdonk, who’s now a respected theoretical physicist at the University of British Columbia.
It’s the standard deep answer of people in the know: Particles are “representations” of “symmetry groups,” which are sets of transformations that can be done to objects.
Take, for example, an equilateral triangle. Rotating it by 120 or 240 degrees, or reflecting it across the line from each corner to the midpoint of the opposite side, or doing nothing, all leave the triangle looking the same as before. These six symmetries form a group. The group can be expressed as a set of mathematical matrices — arrays of numbers that, when multiplied by coordinates of an equilateral triangle, return the same coordinates. Such a set of matrices is a “representation” of the symmetry group.
Samuel Velasco/Quanta Magazine
Similarly, electrons, photons and other fundamental particles are objects that essentially stay the same when acted on by a certain group. Namely, particles are representations of the Poincaré group: the group of 10 ways of moving around in the space-time continuum. Objects can shift in three spatial directions or shift in time; they can also rotate in three directions or receive a boost in any of those directions. In 1939, the mathematical physicist Eugene Wigner identified particles as the simplest possible objects that can be shifted, rotated and boosted.
For an object to transform nicely under these 10 Poincaré transformations, he realized, it must have a certain minimal set of properties, and particles have these properties. One is energy. Deep down, energy is simply the property that stays the same when the object shifts in time. Momentum is the property that stays the same as the object moves through space.
A third property is needed to specify how particles change under combinations of spatial rotations and boosts (which, together, are rotations in space-time). This key property is “spin.” At the time of Wigner’s work, physicists already knew particles have spin, a kind of intrinsic angular momentum that determines many aspects of particle behavior, including whether they act like matter (as electrons do) or as a force (like photons). Wigner showed that, deep down, “spin is just a label that particles have because the world has rotations,” said Nima Arkani-Hamed, a particle physicist at the Institute for Advanced Study in Princeton, New Jersey.
Different representations of the Poincaré group are particles with different numbers of spin labels, or degrees of freedom that are affected by rotations. There are, for example, particles with three spin degrees of freedom. These particles rotate in the same way as familiar 3D objects. All matter particles, meanwhile, have two spin degrees of freedom, nicknamed “spin-up” and “spin-down,” which rotate differently. If you rotate an electron by 360 degrees, its state will be inverted, just as an arrow, when moved around a 2D Möbius strip, comes back around pointing the opposite way.
Samuel Velasco/Quanta Magazine
Elementary particles with one and five spin labels also appear in nature. Only a representation of the Poincaré group with four spin labels seems to be missing.
The correspondence between elementary particles and representations is so neat that some physicists — like Van Raamsdonk’s professor — equate them. Others see this as a conflation. “The representation is not the particle; the representation is a way of describing certain properties of the particle,” said Sheldon Glashow, a Nobel Prize-winning particle theorist and professor emeritus at Harvard University and Boston University. “Let us not confuse the two.”
‘Particles Have So Many Layers’4

Whether there’s a distinction or not, the relationship between particle physics and group theory grew both richer and more complicated over the course of the 20th century. The discoveries showed that elementary particles don’t just have the minimum set of labels needed to navigate space-time; they have extra, somewhat superfluous labels as well.
Particles with the same energy, momentum and spin behave identically under the 10 Poincaré transformations, but they can differ in other ways. For instance, they can carry different amounts of electric charge. As “the whole particle zoo” (as Quinn put it) was discovered in the mid-20th century, additional distinctions between particles were revealed, necessitating new labels dubbed “color” and “flavor.”
Just as particles are representations of the Poincaré group, theorists came to understand that their extra properties reflect additional ways they can be transformed. But instead of shifting objects in space-time, these new transformations are more abstract; they change particles’ “internal” states, for lack of a better word.
Take the property known as color: In the 1960s, physicists ascertained that quarks, the elementary constituents of atomic nuclei, exist in a probabilistic combination of three possible states, which they nicknamed “red,” “green” and “blue.” These states have nothing to do with actual color or any other perceivable property. It’s the number of labels that matters: Quarks, with their three labels, are representations of a group of transformations called SU(3) consisting of the infinitely many ways of mathematically mixing the three labels.
While particles with color are representations of the symmetry group SU(3), particles with the internal properties of flavor and electric charge are representations of the symmetry groups SU(2) and U(1), respectively. Thus, the Standard Model of particle physics — the quantum field theory of all known elementary particles and their interactions — is often said to represent the symmetry group SU(3) × SU(2) × U(1), consisting of all combinations of the symmetry operations in the three subgroups. (That particles also transform under the Poincaré group is apparently too obvious to even mention.)
The Standard Model reigns half a century after its development. Yet it’s an incomplete description of the universe. Crucially, it’s missing the force of gravity, which quantum field theory can’t fully handle. Albert Einstein’s general theory of relativity separately describes gravity as curves in the space-time fabric. Moreover, the Standard Model’s three-part SU(3) × SU(2) × U(1) structure raises questions. To wit: “Where the hell did all this come from?” as Dimitri Nanopoulos put it. “OK, suppose it works,” continued Nanopoulos, a particle physicist at Texas A&M University who was active during the Standard Model’s early days. “But what is this thing? It cannot be three groups there; I mean, ‘God’ is better than this — God in quotation marks.”
Particles ‘Might Be Vibrating Strings’5

In the 1970s, Glashow, Nanopoulos and others tried fitting the SU(3), SU(2) and U(1) symmetries inside a single, larger group of transformations, the idea being that particles were representations of a single symmetry group at the beginning of the universe. (As symmetries broke, complications set in.) The most natural candidate for such a “grand unified theory” was a symmetry group called SU(5), but experiments soon ruled out that option. Other, less appealing possibilities remain in play.
Researchers placed even higher hopes in string theory: the idea that if you zoomed in enough on particles, you would see not points but one-dimensional vibrating strings. You would also see six extra spatial dimensions, which string theory says are curled up at every point in our familiar 4D space-time fabric. The geometry of the small dimensions determines the properties of strings and thus the macroscopic world. “Internal” symmetries of particles, like the SU(3) operations that transform quarks’ color, obtain physical meaning: These operations map, in the string picture, onto rotations in the small spatial dimensions, just as spin reflects rotations in the large dimensions. “Geometry gives you symmetry gives you particles, and all of this goes together,” Nanopoulos said.
However, if any strings or extra dimensions exist, they’re too small to be detected experimentally. In their absence, other ideas have blossomed. Over the past decade, two approaches in particular have attracted the brightest minds in contemporary fundamental physics. Both approaches refresh the picture of particles yet again.
A Particle Is a ‘Deformation of the Qubit Ocean’6

The first of these research efforts goes by the slogan “it-from-qubit,” which expresses the hypothesis that everything in the universe — all particles, as well as the space-time fabric those particles stud like blueberries in a muffin — arises out of quantum bits of information, or qubits. Qubits are probabilistic combinations of two states, labeled 0 and 1. (Qubits can be stored in physical systems just as bits can be stored in transistors, but you can think of them more abstractly, as information itself.) When there are multiple qubits, their possible states can get tangled up, so that each one’s state depends on the states of all the others. Through these contingencies, a small number of entangled qubits can encode a huge amount of information.
In the it-from-qubit conception of the universe, if you want to understand what particles are, you first have to understand space-time. In 2010, Van Raamsdonk, a member of the it-from-qubit camp, wrote an influential essay boldly declaring what various calculations suggested. He argued that entangled qubits might stitch together the space-time fabric.
Calculations, thought experiments and toy examples going back decades suggest that space-time has “holographic” properties: It’s possible to encode all information about a region of space-time in degrees of freedom in one fewer dimension — often on the region’s surface. “In the last 10 years, we’ve learned a lot more about how this encoding works,” Van Raamsdonk said.
What’s most surprising and fascinating to physicists about this holographic relationship is that space-time is bendy because it includes gravity. But the lower-dimensional system that encodes information about that bendy space-time is a purely quantum system that lacks any sense of curvature, gravity or even geometry. It can be thought of as a system of entangled qubits.
Under the it-from-qubit hypothesis, the properties of space-time — its robustness, its symmetries — essentially come from the way 0s and 1s are braided together. The long-standing quest for a quantum description of gravity becomes a matter of identifying the qubit entanglement pattern that encodes the particular kind of space-time fabric found in the actual universe.
So far, researchers know much more about how this all works in toy universes that have negatively curved, saddle-shaped space-time — mostly because they’re relatively easy to work with. Our universe, by contrast, is positively curved. But researchers have found, to their surprise, that anytime negatively curved space-time pops up like a hologram, particles come along for the ride. That is, whenever a system of qubits holographically encodes a region of space-time, there are always qubit entanglement patterns that correspond to localized bits of energy floating in the higher-dimensional world.
Importantly, algebraic operations on the qubits, when translated in terms of space-time, “behave just like rotations acting on the particles,” Van Raamsdonk said. “You realize there’s this picture being encoded by this nongravitational quantum system. And somehow in that code, if you can decode it, it’s telling you that there are particles in some other space.”
The fact that holographic space-time always has these particle states is “actually one of the most important things that distinguishes these holographic systems from other quantum systems,” he said. “I think nobody really understands the reason why holographic models have this property.”
It’s tempting to picture qubits having some sort of spatial arrangement that creates the holographic universe, just as familiar holograms project from spatial patterns. But in fact, the qubits’ relationships and interdependencies might be far more abstract, with no real physical arrangement at all. “You don’t need to talk about these 0s and 1s living in a particular space,” said Netta Engelhardt, a physicist at MIT who recently won a New Horizons in Physics Prize for calculating the quantum information content of black holes. “You can talk about the abstract existence of 0s and 1s, and how an operator might act on 0s and 1s, and these are all much more abstract mathematical relations.”
There’s clearly more to understand. But if the it-from-qubit picture is right, then particles are holograms, just like space-time. Their truest definition is in terms of qubits.
‘Particles Are What We Measure in Detectors’7
Another camp of researchers who call themselves “amplitudeologists” seeks to return the spotlight to the particles themselves.
These researchers argue that quantum field theory, the current lingua franca of particle physics, tells far too convoluted a story. Physicists use quantum field theory to calculate essential formulas called scattering amplitudes, some of the most basic calculable features of reality. When particles collide, amplitudes indicate how the particles might morph or scatter. Particle interactions make the world, so the way physicists test their description of the world is to compare their scattering amplitude formulas to the outcomes of particle collisions in experiments such as Europe’s Large Hadron Collider.
Nima Arkani-Hamed investigates the relationship between particle behavior and geometric objects.
Béatrice de Géa for Quanta Magazine
Normally, to calculate amplitudes, physicists systematically account for all possible ways colliding ripples might reverberate through the quantum fields that pervade the universe before they produce stable particles that fly away from the crash site. Strangely, calculations involving hundreds of pages of algebra often yield, in the end, a one-line formula. Amplitudeologists argue that the field picture is obscuring simpler mathematical patterns. Arkani-Hamed, a leader of the effort, called quantum fields “a convenient fiction.” “In physics very often we slip into a mistake of reifying a formalism,” he said. “We start slipping into the language of saying that it’s the quantum fields that are real, and particles are excitations. We talk about virtual particles, all this stuff — but it doesn’t go click, click, click in anyone’s detector.”
Amplitudeologists believe that a mathematically simpler and truer picture of particle interactions exists.
In some cases, they’re finding that Wigner’s group theory perspective on particles can be extended to describe interactions as well, without any of the usual rigmarole of quantum fields.
Lance Dixon, a prominent amplitudeologist at the SLAC National Accelerator Laboratory, explained that researchers have used the Poincaré rotations studied by Wigner to directly deduce the “three-point amplitude” — a formula describing one particle splitting into two. They’ve also shown that three-point amplitudes serve as the building blocks of four- and higher-point amplitudes involving more and more particles. These dynamical interactions seemingly build from the ground up out of basic symmetries.
“The coolest thing,” according to Dixon, is that scattering amplitudes involving gravitons, the putative carriers of gravity, turn out to be the square of amplitudes involving gluons, the particles that glue together quarks. We associate gravity with the fabric of space-time itself, while gluons move around in space-time. Yet gravitons and gluons seemingly spring from the same symmetries. “That’s very weird and of course not really understood in quantitative detail because the pictures are so different,” Dixon said.
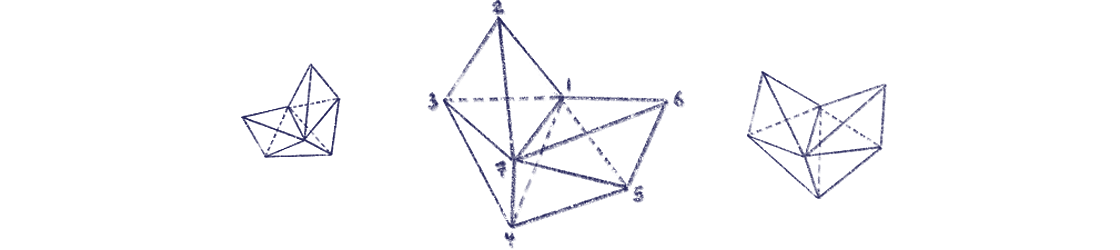
Arkani-Hamed and his collaborators, meanwhile, have found entirely new mathematical apparatuses that jump straight to the answer, such as the amplituhedron — a geometric object that encodes particle scattering amplitudes in its volume. Gone is the picture of particles colliding in space-time and setting off chain reactions of cause and effect. “We’re trying to find these objects out there in the Platonic world of ideas that give us [causal] properties automatically,” Arkani-Hamed said. “Then we can say, ‘Aha, now I can see why this picture can be interpreted as evolution.’”
It-from-qubit and amplitudeology approach the big questions so differently that it’s hard to say whether the two pictures complement or contradict each other. “At the end of the day, quantum gravity has some mathematical structure, and we’re all chipping away at it,” Engelhardt said. She added that a quantum theory of gravity and space-time will ultimately be needed to answer the question, “What are the fundamental building blocks of the universe on its most fundamental scales?” — a more sophisticated phrasing of my question, “What is a particle?”
In the meantime, Engelhardt said, “‘We don’t know’ is the short answer.”
1: “At the moment that I detect it, it collapses the wave and becomes a particle. … [The particle is] the collapsed wave function.”
—Dimitri Nanopoulos (back to article)
2: “What is a particle from a physicist’s point of view? It’s a quantum excitation of a field. We write particle physics in a math called quantum field theory. In that, there are a bunch of different fields; each field has different properties and excitations, and they are different depending on the properties, and those excitations we can think of as a particle.”
—Helen Quinn (back to article)
3: “Particles are at a very minimum described by irreducible representations of the Poincaré group.”
— Sheldon Glashow
“Ever since the fundamental paper of Wigner on the irreducible representations of the Poincaré group, it has been a (perhaps implicit) definition in physics that an elementary particle ‘is’ an irreducible representation of the group, G, of ‘symmetries of nature.’”
—Yuval Ne’eman and Shlomo Sternberg (back to article)
4: “Particles have so many layers.”
—Xiao-Gang Wen (back to article)
5: “What we think of as elementary particles, instead they might be vibrating strings.”
—Mary Gaillard (back to article)
6: “Every particle is a quantized wave. The wave is a deformation of the qubit ocean.”
—Xiao-Gang Wen (back to article)
7: “Particles are what we measure in detectors. … We start slipping into the language of saying that it’s the quantum fields that are real, and particles are excitations. We talk about virtual particles, all this stuff — but it doesn’t go click, click, click in anyone’s detector.”
—Nima Arkani-Hamed (back to article)
Editor’s note: Mark Van Raamsdonk receives funding from the Simons Foundation, which also funds this editorially independent magazine. Simons Foundation funding decisions have no influence on our coverage. More details are available here.



