Why e, the Transcendental Math Constant, Is Just the Best

James Round for Quanta Magazine
Introduction
Last month, we presented three puzzles that seemed ordinary enough but contained a numerical twist. Hidden below the surface was the mysterious transcendental number e. Most familiar as the base of natural logarithms, Euler’s number e is a universal constant with an infinite decimal expansion that begins with 2.7 1828 1828 45 90 45… (spaces added to highlight the quasi-pattern in the first 15 digits after the decimal point). But why, in our puzzles, does it seemingly appear out of nowhere?
Before we attempt to answer this question, we need to learn a little more about e’s properties and aliases. Like its transcendental cousin π, e can be represented in countless ways — as the sum of infinite series, an infinite product, a limit of infinite sequences, an amazingly regular continued fraction, and so on.
I still remember my first introduction to e. We were studying common logarithms in school, and I marveled at their ability to turn complicated multiplication problems into simple addition just by representing all numbers as fractional powers of 10. How, I wondered, were fractional and irrational powers calculated? It is, of course, easy to calculate integer powers such as 102 and 103, and in a pinch you could even calculate 102.5 by finding the square root of 105. But how did they figure out, as the log table asserted, that 20 was 101.30103? How could a complete table of logarithms of all numbers be constructed from scratch? I just couldn’t imagine how that could be done.
Later I learned about the magic formula that enables this feat. It gives a hint of where the “natural” in “natural logarithms” came from:
ex = 1 + $latex \frac{x}{1 !}+\frac{x^{2}}{2 !}+\frac{x^{3}}{3 !}+\frac{x^{4}}{4 !}+\frac{x^{5}}{5 !}+\cdots$.
For negative powers, alternate terms are negative as expected:
e-x = 1 – $latex \frac{x}{1 !}+\frac{x^{2}}{2 !}-\frac{x^{3}}{3 !}+\frac{x^{4}}{4 !}-\frac{x^{5}}{5 !}+\cdots$.
These powerful formulas enable the calculation of any power of the mysterious e for any real number, integer or fraction from negative infinity to infinity, to any desired precision. They allow the construction of a complete table of natural logarithms and, from that, common logarithms, from scratch.
The special case of this formula for x = 1 gives this famous representation of e:
e = 1 + $latex \frac{1}{1 !}+\frac{1}{2 !}+\frac{1}{3 !}+\frac{1}{4 !}+\frac{1}{5 !}+\cdots$.
In addition, e has many amazing properties, some of which we’ll uncover in the solutions to our problems. But the one property that goes to the essence of e and makes it so natural for logarithms and situations of exponential growth and decay is this:
$latex \frac{d}{dx}$ex = ex.
This says that the rate of change of ex is equal to its value at all points. When x represents time, it signifies a rate of growth (or decay, for negative x) that is equal to the size or quantity that has accumulated thus far. There are myriad phenomena in the real world that do exactly this for stretches of time, and we know them as examples of exponential growth or decay. But, utility apart, there is an element of aesthetic perfection and naturalness in this property of e that can truly inspire wonder. It even carries a moral lesson; I like to think of it as a Zen-like function that, in its quest for growth, is always in perfect balance, never reaching out for more or less than what it has earned.
A word of warning: In the puzzle solutions below, we will get into math that’s a bit more advanced and formidable-looking than is normal for this puzzle column. Don’t worry if the equations make your eyes glaze over; just try to follow the general argument and concepts. My hope is that anyone can come away with some insight, however hazy, about how and why e appears in our puzzles. In the BBC TV series The Ascent of Man, Jacob Bronowski said of John von Neumann’s mathematical writing that it is important when reading math to follow the tune of the conceptual argument — the equations are merely the “orchestration down in the bass.”
Now let us try and track down how e appears in our puzzles.
Puzzle 1: Partition
Let’s take any number, such as 10. Divide it into some number of identical pieces, such as two 5s, and multiply them together: 5 × 5 = 25. Now, we could have divided 10 into three, four, five or six identical pieces and done the same. Here’s what happens to our product when we do so:
2 pieces: 5 × 5 = 25
3 pieces: 3.33 × 3.33 × 3.33 = 37.04
4 pieces: 2.5 × 2.5 × 2.5 × 2.5 = 39.06
5 pieces: 2 × 2 × 2 × 2 × 2 = 32
6 pieces: 1.67 × 1.67 × 1.67 × 1.67 × 1.67 × 1.67 = 21.43
You can see that the product increases, reaches what seems to be a maximum and then starts decreasing. Try doing the same with some other numbers such as 20 and 30. You’ll notice that the same thing happens in every case. This has nothing to do with the numbers themselves but is caused by a unique property of the number e.
a. See if you can figure out when the product reaches a maximum for a given number and what this has to do with e.
As I mentioned in the hint for 1a, the product reaches a maximum when the value of each piece is closest to e. To be more accurate, the two highest products will be obtained when the values of the pieces lie on either side of e. For the small, everyday-size numbers we are considering here, the highest value is obtained for the piece whose difference from e is the smallest.
b. For the number 10, the largest product (39.06) is about 5.5% larger than the next largest (37.04). Without calculating the actual difference, can you guess which number less than 100 has the smallest percentage difference between the largest product and the next largest? Why should this be?
From above, it is easy to see that two products will be closest together when the values of the two adjacent pieces are almost equidistant from e, one lower than e and the other higher. (This is strictly true only if the function is symmetric around e, which it is not, but in this range it is close enough, as Michel Nizette explained excellently.) If the original number is N, this will tend to happen when the fractional part of the ratio $latex \frac{N}{e}$ is close to 0.5 — that is, when $latex \frac{N}{e}$ lies close to the midpoint between two integers. So if you construct a table of $latex \frac{N}{e}$ for N up to 100 and look for the fractional part closest to 0.5, you will get the required integer: 53. Dividing 53 by e gives 19.4976 and a difference of only 0.0013% for the products yielded by 19 and 20 pieces.
c. Can you explain why e arises in this apparently simple problem?
As explained by readers Lazar Ilic, Ashok Khatri, Alan Olson, Kurt Godel, TG, Atul Kumar and Michel Nizette, the answer involves some elementary calculus — specifically, you need to find the maximum of a function by setting its derivative to zero. Our function is ($latex \frac{n}{x}$)x, and the value of each piece is $latex \frac{n}{x}$. The logarithm of the function is x(ln $latex \frac{n}{x}$), and we can maximize that instead, which is somewhat easier. If you can solve this manually, kudos to you! But if doing calculus is not your cup of tea, you can just type “d/dx(x ln n/x) = 0″ into Wolfram Alpha. The derivative evaluates as ln($latex \frac{n}{x}$) = 1, and out pops the solution x = $latex \frac{n}{e}$ for positive n and x. Thus, the value of the optimal piece is $latex \frac{n}{x}$ = e. Voila! That’s how e arises and gives the maximum product.
This teaches us that e has a property of optimality. It can pop up in situations that involve finding a maximum or minimum, as we will see in puzzle 2. The most basic version of this property of e is seen if you calculate the value of the function x1/x for all positive real numbers (this is known as Steiner’s problem). Of all the infinite real numbers, the x that yields the highest value for this function is e. Maximizing x1/x is equivalent to maximizing $latex \frac{(\ln x)}{x}$, whose derivative $latex \frac{(1 -\ln x)}{x^2}$ is zero at ln x = 1, when x = e.
Puzzle 2: Union
As readers pointed out, this was a restatement of the well-known secretary problem. The essential points are summarized below.
An heir has to choose the best of 10 potential candidate spouses under the following rules. The candidates are interviewed one after another, and either accepted (if suspected to be the best) or rejected before the next candidate is considered. A rejected candidate cannot be recalled, and once a candidate is accepted the process stops. The last candidate must be accepted by default if the process has not ended by then.
a. How can the heir maximize his chances of choosing the best candidate, assuming there are no ties?
This situation requires the heir to reject a specific number of candidates unconditionally (the “rejection” phase) followed by a “selection phase” in which he selects the first one among the remaining candidates who ranks higher than all of the previously rejected ones. The chances of choosing the best candidate are maximized when the rejection phase is a specific length. The probability falls off if the rejection phase is longer (the best candidate may be more likely to be rejected) or shorter (he doesn’t have enough experience to rank the candidates properly, resulting in acceptance of lower-ranked candidates).
This is known as an “optimal stopping” problem, and e appears in its solution because of its property of optimality. For a large number of candidates n, the optimal number of candidates rejected initially should be equal to n divided by e.
Here are the probability calculations for n = 10 if the rejection phase (r) = 3. First, note that the best candidate could turn up at any point in the series of 10 interviews, with a 1-in-10 probability ($latex \frac{1}{n}$) of being in any particular position. For each interviewee’s position (i), we multiply this $latex \frac{1}{10}$ by the probability that the best candidate will be selected at that position. Then we sum the probabilities for all the positions and build our general expression.
- If the best candidate is at positions 1 to 3, they will be automatically rejected. Probability (p) of selecting the best candidate = $latex \frac{1}{10}$ × 0 = 0.
- If the best candidate is at position 4, they will always be selected. Probability p of this outcome = $latex \frac{1}{10}$ × 1 = $latex \frac{1}{10}$ = $latex \frac{1}{n}$.
- At position 5, the candidate will be selected if the previous highest-ranking candidate is in positions 1 to 3, but not 4. So p = $latex \frac{1}{10}$ × $latex \frac{3}{4}$ = $latex \frac{1}{n}$ × $latex \frac{r}{(i – 1)}$ = $latex \frac{r}{n}$ × $latex \frac{1}{(i – 1)}$.
- At position 6, the candidate is selected if the previous highest-ranking candidate is in positions 1 to 3, but not 4 or 5. So p = $latex \frac{1}{10}$ × $latex \frac{3}{5}$ = $latex \frac{1}{n}$ × $latex \frac{r}{(i – 1)}$ = $latex \frac{r}{n}$ × $latex \frac{1}{(i – 1)}$.
- …
- At position 10, p = $latex \frac{1}{10}$ × $latex \frac{3}{9}$ = $latex \frac{1}{n}$ × $latex \frac{r}{(i – 1)}$ = $latex \frac{r}{n}$ × $latex \frac{1}{(i – 1)}$.
As you can see, we get the same expression for each position in the selection phase: $latex \frac{r}{n}$ × $latex \frac{1}{(i – 1)}$. (The expression for position 4 can be written as $latex \frac{1}{10}$ × $latex \frac{3}{3}$ = $latex \frac {r}{n}$ × $latex \frac{1}{(i – 1)}$ to fit the pattern.)
Taking $latex \frac{r}{n}$ out of the summation sign, this sum — the probability of finding the best candidate — can be written:
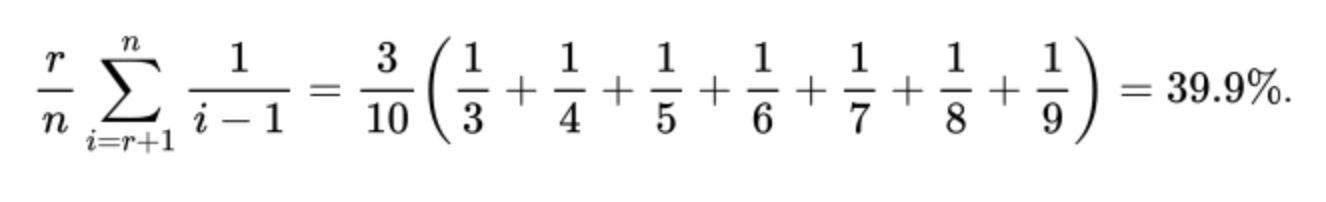
The corresponding probability of finding the best candidate for r = 4 initial candidates rejected is 39.8%. These are the two highest values, and the probability falls away for greater or fewer initial rejections. Does this remind you of the partition puzzle? That’s no coincidence, as we’ll see below.
b. How do the heir’s chances change if there is a 10% chance of a tie for first place?
Since the heir now has two equally ranked candidates 10% of the time, the chances of finding the best candidate increase.
c. This problem is a classical one whose solution has something to do with e. Can you explain how e enters the picture?
It turns out e enters the picture twice in this problem! As the number n becomes large, Euler’s number appears both in the probability of finding the best choice and in the proportion of initial cases to reject.
The probability expression we derived above can be represented, as n grows to infinity, by an integral by substituting x for the limit of $latex \frac{r}{n}$ (the rejection fraction), p for $latex \frac{(i – 1)}{n}$ (the incremental probability at each n) and dp for $latex \frac{1}{n}$ (the rate of change from one integer to the next). This gives the limit of the probability as:
$latex x \int_{x}^{1} \frac{1}{p} d p=-x \ln x$.
Again, the expression on the right-hand side is similar to the ones we looked at in the partition problem. Setting the derivative to zero, we find that both the optimal fraction of candidates that should be rejected and the probability of making the best choice are $latex \frac{1}{e}$, or about 36.8%.
d. How can the heir achieve the highest expected rank of his chosen candidate in this more practical choosing scenario?
In the classical scenario above, the heir adopts an all-or-nothing strategy by rejecting the first few candidates and then selecting the first one that betters all the rejected ones. While this does maximize the probability of finding the best candidate, it may also result in his being stuck with a low-ranked candidate if the best candidate was among the initial rejects. To avoid this, his best practical strategy is to be very picky to begin with and look for the very best candidates, and then reduce pickiness by settling for merely good candidates as the number of candidates runs out.
This strategy can be made precise by starting backward from when only the last candidate is left. This person could slot in anywhere in the ranking with equal probability. So the expectation is that their final rank will be average (5.5 in this case). So you should accept the second-to-last candidate if they would be in your top five up to this point, even though they may not be the absolute best. When two candidates are left, the expectation for the higher-ranked one of the two will be at about 3.67, so for the third-to-last candidate you should be satisfied with a candidate who is within the top three. By calculating exactly how picky you need to be at every stage, you have a better chance of getting a very good candidate than by using the classical algorithm.
Puzzle 3: Togetherness
A large auditorium is staging a show that admits couples only. When a couple enters the auditorium, they pick at random a pair of seats next to each other. Each new couple does the same, and in many cases this results in empty single seats between couples. The seating continues until only single seats are left. Then the auditorium is declared full, and the show starts.
a. What proportion of seats are expected to be left unfilled when the seating is stopped?
The answer, as the number of seats increases, approaches $latex \frac{1}{e^2}$, or about 13.5%.
b. How does e enter this theater of togetherness?
Let’s see what happens when there are a small number of seats labeled alphabetically. Let’s call the numbers of expected empty seats E1, E2, E3, E4, and so on, where the subscripts are the number of empty chairs in a row.
- A single seat is empty: A couple cannot occupy it, so E1 = 1.
- For two seats, there is no empty seat, so E2 is 0.
- For three seats, the couple can occupy AB or BC, leaving one seat empty in each case, so E3 = 1.
- For four seats, a couple may occupy BC, leaving two empty seats, or they can occupy AB or CD, leaving none. This gives three configurations yielding a total of two empty seats, giving an average expectation of E4 = $latex \frac{2}{3}$.
By playing with the relationships between these and the next few numbers, Lazar Ilic and Michel Nizette were able to derive a recurrence relation that allowed them to predict the unfilled seats for the current number of seats (n) using previous results for n – 1 and n – 2 seats. The formula for the recurrence relation is (for n ≥ 2):
(n − 1)En = 2nEn−2 + (n − 2)En-1.
The sequence goes: 1, 0, 1,$latex \frac{2}{3}$, 1,$latex \frac{16}{15}$,$latex \frac{11}{9}$,$latex \frac{142}{105}$ …
These numbers divided by the number of seats give the proportion of unfilled seats, which Nizette calculated as being 16.24% for 10 seats, 13.804% for 100, 13.561% for 1,000, and 13.538% for 6,000. You can see that the numbers are approaching $latex \frac{1}{e^2}$ or 13.5335…%. But how can we know that’s exactly where they are headed for huge numbers for which the relation will take too long to calculate?
A recurrence relation is good, but it is like trying to climb an infinite staircase one step at a time. What we really need is a closed-form expression that depends only on n. A closed-form expression is like an elevator. You press the button for any n, and whoosh! — the elevator takes you there, including right to the top of the building where the view is infinite.
Obtaining a closed formula from a recurrence relation is called solving the recurrence. There is no magic bullet for this, and although there are some techniques you can try, it is something of an art. Math programs such as Mathematica have packages for this. For our problem, Lazar Ilic produced a closed-form expression for En that showed that the limit of $latex \frac{1}{e^2}$was correct.
So e does enter the theater, but how? We still don’t have an inkling how it got there. Which of its numerous superpowers did it use? Below, I try to give an intuitive glimpse of the main highlights while leaving out the thickets of tangled algebra in between.
First, let’s derive two difference sequences starting with our sequence E. The first-order difference sequence D consists of differences between consecutive values of E, and the second-order difference sequence DD consists of differences between consecutive values of D. Thus D1 = E1 − E0, D2 = E2 − E1, D3 = E3 − E2, and so on, and DD1 = D1 − D0, DD2 = D2 − D1, DD3 = D3 − D2, and so on. (Both E0 and D0 are 0). I’ll explain the point of doing all this shortly. The initial values of all three sequences are listed in the table below.
| n | Expected empty seats E | Value | 1st Diff. Seq. D | Value | 2nd Diff. Seq. DD | Value |
| 0 | E0 | 0 | D0 | 0 | DD0 | 0 |
| 1 | E1 | 1 | D1 = E1 – E0 |
1 | DD1 = D1 – D0 |
1 |
| 2 | E2 | 0 | D2 = E2 – E1 |
-1 | DD2 = D2 – D1 |
-2 |
| 3 | E3 | 1 | D3 = E3 – E2 |
1 | DD3 = D3 – D2 |
2 |
| 4 | E4 | $latex \frac{2}{3}$ | D4 = E4 – E3 |
-$latex \frac{1}{3}$ | DD4 = D4 – D3 |
-$latex \frac{4}{3}$ |
| 5 | E5 | 1 | D5 = E5 – E4 |
$latex \frac{1}{3}$ | DD5 = D5 – D4 |
$latex \frac{2}{3}$ |
| 6 | E6 | $latex \frac{16}{15}$ | D6 = E6 – E5 |
$latex \frac{1}{15}$ | DD6 = D6 – D5 |
-$latex \frac{4}{15}$ |
| 7 | E7 | $latex \frac{11}{9}$ | D7 = E7 – E6 |
$latex \frac{7}{45}$ | DD7 = D7 – D6 |
$latex \frac{4}{45}$ |
By doing some tangled algebra on the original recurrence relation, we can derive a closed-form expression for DDn as follows (n ≥ 1):
DDn = $latex\frac{(-2)^{n-1}}{(n-1) !}$
We can verify that this formula works by comparing it with the above table:
DD1 = $latex\frac{(-2)^{0}}{0 !}$ = 1
DD2 = $latex\frac{(-2)^{1}}{1 !}$ = -2
DD3 = $latex\frac{(-2)^{2}}{2 !}$ = 2
DD4 = $latex\frac{(-2)^{3}}{3 !}$ = -$latex \frac{8}{6}$ = -$latex \frac{4}{3}$
DD5 = $latex\frac{(-2)^{4}}{4 !}$ = $latex \frac{16}{24}$ = $latex \frac{2}{3}$
DD6 = $latex\frac{(-2)^{5}}{5 !}$ = -$latex \frac{32}{120}$ = -$latex \frac{4}{15}$
DD7 = $latex\frac{(-2)^{6}}{6 !}$ = $latex \frac{64}{720}$ = $latex \frac{4}{45}$
Now here’s the kicker: Notice what happens when you add up all the DDs.
DD1 + DD2 + DD3 + … + DDn−1 + DDn =
D1 − D0 + D2 − D1 + D3 − D2 + … + Dn−1 − Dn−2 + Dn − Dn−1 = Dn − 0 = Dn.
All the other terms cancel, leaving only Dn. This technique of solving a recurrence is aptly called telescoping.
Now let’s plug the closed-form expressions back in for each of the DDs.
Dn = 1 – $latex\frac{2}{1 !}+\frac{2^{2}}{2 !}-\frac{2^{3}}{3 !}+\frac{2^{4}}{4 !}-\frac{2^{5}}{5 !}+\cdots$.
Look familiar? Compare this to the infinite series for e-x above. In fact, for large n, this is exactly the formula for e-2 or $latex\frac{1}{e^2}$.
So the square of our transcendental constant has magically appeared in the denominator of the first difference sequence derived from the number of empty seats. It’s there because the process entails a summation of successive powers of −2 divided by the corresponding factorial, which is exactly the structure of the powers of e.
We still have some work to do to get back from the D sequence to the E sequence by a similar process to get En. This value, divided by n, will give us the fraction of seats that are empty. To get to the finish line, we need to do some more tangled algebra. Suffice it to say that e−2 remains in the final expression, which looks like this:
$latex \frac{E_{n}}{n}=\frac{1}{e^{2}}+\frac{2}{e^{2}}\left(\frac{1}{n}\right)+\cdots$
In the limit of large n, only the first term remains, giving the result we already found: $latex \frac{1}{e^2}$. Note that for the large but finite numbers that Michel Nizette listed, just the sum of the first two terms fits values for the unfilled fraction almost exactly.
I hope you enjoyed the heavy dose of transcendence from this most fascinating and fundamental constant. The Quanta Insights award for this month goes jointly to Michel Nizette, for clarity of exposition, and Lazar Ilic for the usual mathematical mastery. Congratulations to both!
(Lazar Ilic, you are clearly one of the best mathematicians to grace the comments sections of our puzzles. As this is the third time you have won this award, by my count, and we want to give others a chance too, this is the final award we will bestow on you. You have hereby entered the Insights Hall of Fame. I do hope you will keep contributing your deeply insightful comments. We look forward to them.)
See you next time for new Insights!



