How Feynman Diagrams Almost Saved Space

Richard Feynman looked tired when he wandered into my office. It was the end of a long, exhausting day in Santa Barbara, sometime around 1982. Events had included a seminar that was also a performance, lunchtime grilling by eager postdocs, and lively discussions with senior researchers. The life of a celebrated physicist is always intense. But our visitor still wanted to talk physics. We had a couple of hours to fill before dinner.
I described to Feynman what I thought were exciting if speculative new ideas such as fractional spin and anyons. Feynman was unimpressed, saying: “Wilczek, you should work on something real.” (Anyons are real, but that’s a topic for another post.)
Quantized
A monthly column in which top researchers explore the process of discovery. This month’s columnist, Frank Wilczek, is a Nobel Prize-winning physicist at the Massachusetts Institute of Technology.
Looking to break the awkward silence that followed, I asked Feynman the most disturbing question in physics, then as now: “There’s something else I’ve been thinking a lot about: Why doesn’t empty space weigh anything?”
Feynman, normally as quick and lively as they come, went silent. It was the only time I’ve ever seen him look wistful. Finally he said dreamily, “I once thought I had that one figured out. It was beautiful.” And then, excited, he began an explanation that crescendoed in a near shout: “The reason space doesn’t weigh anything, I thought, is because there’s nothing there!”
To appreciate that surreal monologue, you need to know some backstory. It involves the distinction between vacuum and void.
Vacuum, in modern usage, is what you get when you remove everything that you can, whether practically or in principle. We say a region of space “realizes vacuum” if it is free of all the different kinds of particles and radiation we know about (including, for this purpose, dark matter — which we know about in a general way, though not in detail). Alternatively, vacuum is the state of minimum energy.
Intergalactic space is a good approximation to a vacuum.
Void, on the other hand, is a theoretical idealization. It means nothingness: space without independent properties, whose only role, we might say, is to keep everything from happening in the same place. Void gives particles addresses, nothing more.
Aristotle famously claimed that “Nature abhors a vacuum,” but I’m pretty sure a more correct translation would be “Nature abhors a void.” Isaac Newton appeared to agree when he wrote:
… that one Body may act upon another at a Distance thro’ a Vacuum, without the Mediation of any thing else, by and through which their Action and Force may be conveyed from one to another, is to me so great an Absurdity, that I believe no Man who has in philosophical Matters a competent Faculty of thinking, can ever fall into it.
But in Newton’s masterpiece, the Principia, the players are bodies that exert forces on one another. Space, the stage, is an empty receptacle. It has no life of its own. In Newtonian physics, vacuum is a void.
That Newtonian framework worked brilliantly for nearly two centuries, as Newton’s equations for gravity went from triumph to triumph, and (at first) the analogous ones for electric and magnetic forces seemed to do so as well. But in the 19th century, as people investigated the phenomena of electricity and magnetism more closely, Newton-style equations proved inadequate. In James Clerk Maxwell’s equations, the fruit of that work, electromagnetic fields — not separated bodies — are the primary objects of reality.
Quantum theory amplified Maxwell’s revolution. According to quantum theory, particles are merely bubbles of froth, kicked up by underlying fields. Photons, for example, are disturbances in electromagnetic fields.
As a young scientist, Feynman found that view too artificial. He wanted to bring back Newton’s approach and work directly with the particles we actually perceive. In doing so, he hoped to challenge hidden assumptions and reach a simpler description of nature — and to avoid a big problem that the switch to quantum fields had created.
II.
In quantum theory, fields have a lot of spontaneous activity. They fluctuate in intensity and direction. And while the average value of the electric field in a vacuum is zero, the average value of its square is not zero. That’s significant because the energy density in an electric field is proportional to the field’s square. The energy density value, in fact, is infinite.
The spontaneous activity of quantum fields goes by several different names: quantum fluctuations, virtual particles, or zero-point motion. There are subtle differences in the connotations of these expressions, but they all refer to the same phenomenon. Whatever you call it, the activity involves energy. Lots of energy — in fact, an infinite amount.
For most purposes we can leave that disturbing infinity out of consideration. Only changes in energy are observable. And because zero-point motion is an intrinsic characteristic of quantum fields, changes in energy, in response to external events, are generally finite. We can calculate them. They give rise to some very interesting effects, such as the Lamb shift of atomic spectral lines and the Casimir force between neutral conducting plates, which have been observed experimentally. Far from being problematic, those effects are triumphs for quantum field theory.
The exception is gravity. Gravity responds to all kinds of energy, whatever form that energy may take. So the infinite energy density associated with the activity of quantum fields, present even in a vacuum, becomes a big problem when we consider its effect on gravity.
In principle, those quantum fields should make the vacuum heavy. Yet experiments tell us that the gravitational pull of the vacuum is quite small. Until recently — see more on this below — we thought it was zero.
Perhaps Feynman’s conceptual switch from fields to particles would avoid the problem.
III.
Feynman started from scratch, drawing pictures whose stick-figure lines show links of influence between particles. The first published Feynman diagram appeared in Physical Review in 1949:
To understand how one electron influences another, using Feynman diagrams, you have to imagine that the electrons, as they move through space and evolve in time, exchange a photon, here labeled “virtual quantum.” This is the simplest possibility. It is also possible to exchange two or more photons, and Feynman made similar diagrams for that. Those diagrams contribute another piece to the answer, modifying the classical Coulomb force law. By sprouting another squiggle, and letting it extend freely into the future, you represent how an electron radiates a photon. And so, step by step, you can describe complex physical processes, assembled like Tinkertoys from very simple ingredients.
Feynman diagrams look to be pictures of processes that happen in space and time, and in a sense they are, but they should not be interpreted too literally. What they show are not rigid geometric trajectories, but more flexible, “topological” constructions, reflecting quantum uncertainty. In other words, you can be quite sloppy about the shape and configuration of the lines and squiggles, as long as you get the connections right.
Feynman found that he could attach a simple mathematical formula to each diagram. The formula expresses the likelihood of the process the diagram depicts. He found that in simple cases he got the same answers that people had obtained much more laboriously using fields when they let froth interact with froth.
That’s what Feynman meant when he said, “There’s nothing there.” By removing the fields, he’d gotten rid of their contribution to gravity, which had led to absurdities. He thought he’d found a new approach to fundamental interactions that was not only simpler than the conventional one, but also sounder. It was a beautiful new way to think about fundamental processes.
IV.
Sadly, first appearances proved deceptive. As he worked things out further, Feynman discovered that his approach had a similar problem to the one it was supposed to solve. You can see this in the pictures below. We can draw Feynman diagrams that are completely self-contained, without particles to initiate the events (or to flow out from them). These so-called disconnected graphs, or vacuum bubbles, are the Feynman diagram analogue of zero-point motion. You can draw diagrams for how virtual quanta affect gravitons, and thereby rediscover the morbid obesity of “empty” space.
More generally, as he worked things out further, Feynman gradually realized — and then proved — that his diagram method is not a true alternative to the field approach, but rather an approximation to it. To Feynman, that came as a bitter disappointment.
Yet Feynman diagrams remain a treasured asset in physics, because they often provide good approximations to reality. Plus, they’re easy (and fun) to work with. They help us bring our powers of visual imagination to bear on worlds we can’t actually see.
The calculations that eventually got me a Nobel Prize in 2004 would have been literally unthinkable without Feynman diagrams, as would my calculations that established a route to production and observation of the Higgs particle.
On that day in Santa Barbara, citing those examples, I told Feynman how important his diagrams had been to me in my work. He seemed pleased, though he could hardly have been surprised at his diagrams’ importance. “Yeah, that’s the good part, seeing people use them, seeing them everywhere,” he replied with a wink.
V.
The Feynman diagram representation of a process is most useful when a few relatively simple diagrams supply most of the answer. That is the regime physicists call “weak coupling,” where each additional complicating line is relatively rare. That is almost always the case for photons in quantum electrodynamics (QED), the application Feynman originally had in mind. QED covers most of atomic physics, chemistry and materials science, so it’s an amazing achievement to capture its essence in a few squiggles.
As an approach to the strong nuclear force, however, this strategy fails. Here the governing theory is quantum chromodynamics (QCD). The QCD analogues of photons are particles called color gluons, and their coupling is not weak. Usually, when we do a calculation in QCD, a host of complicated Feynman diagrams — festooned with many gluon lines — make important contributions to the answer. It’s impractical (and probably impossible) to add them all up.
On the other hand, with modern computers we can go back to the truly fundamental field equations and calculate fluctuations in the quark and gluon fields directly. This approach gives beautiful pictures of another kind:
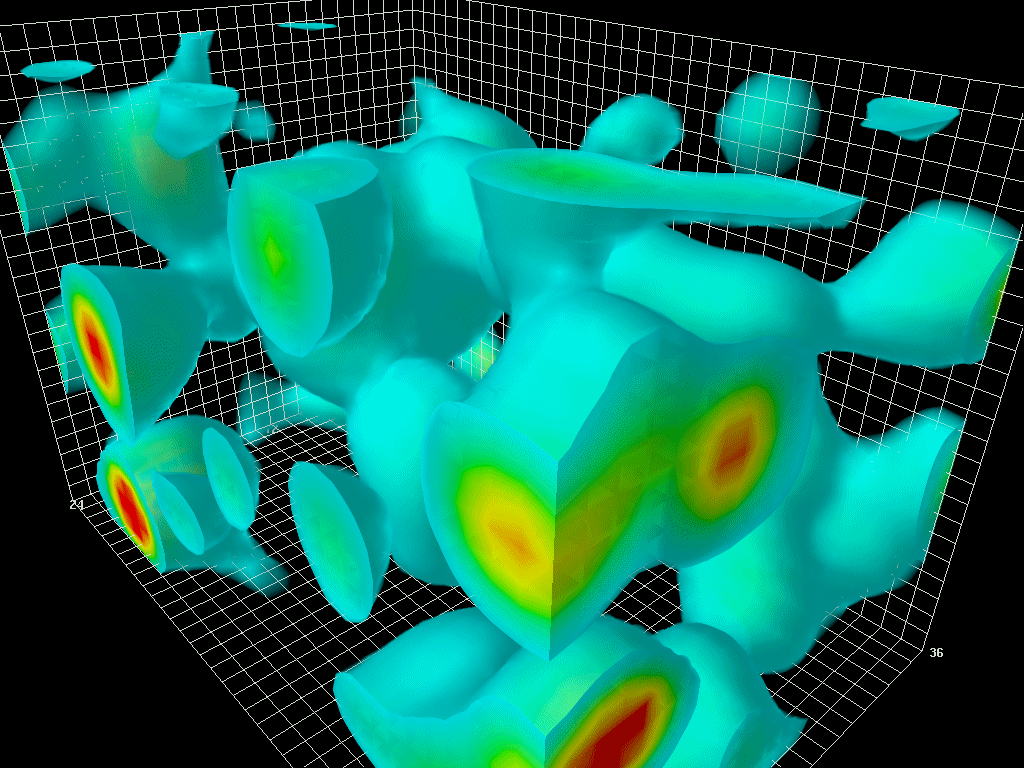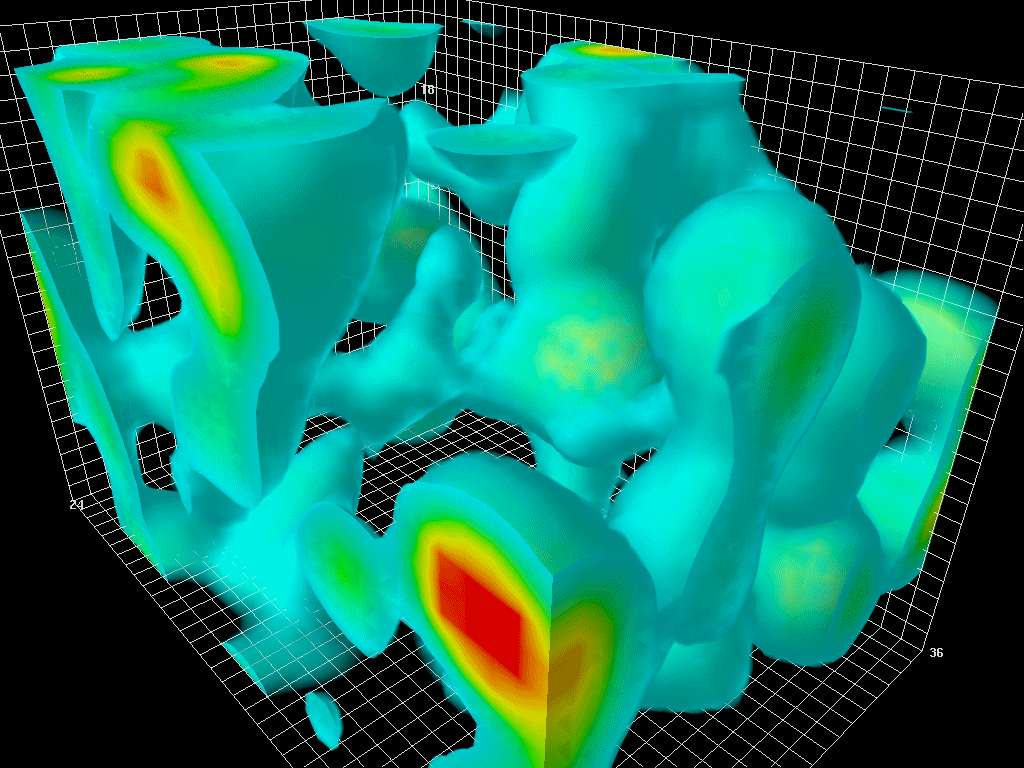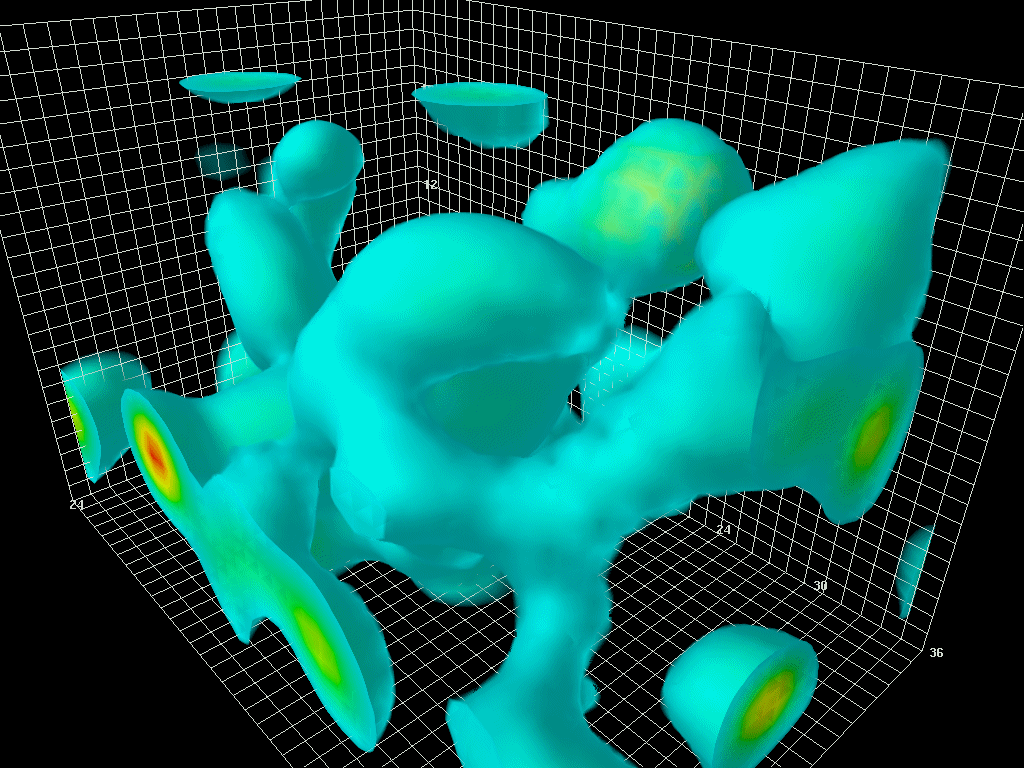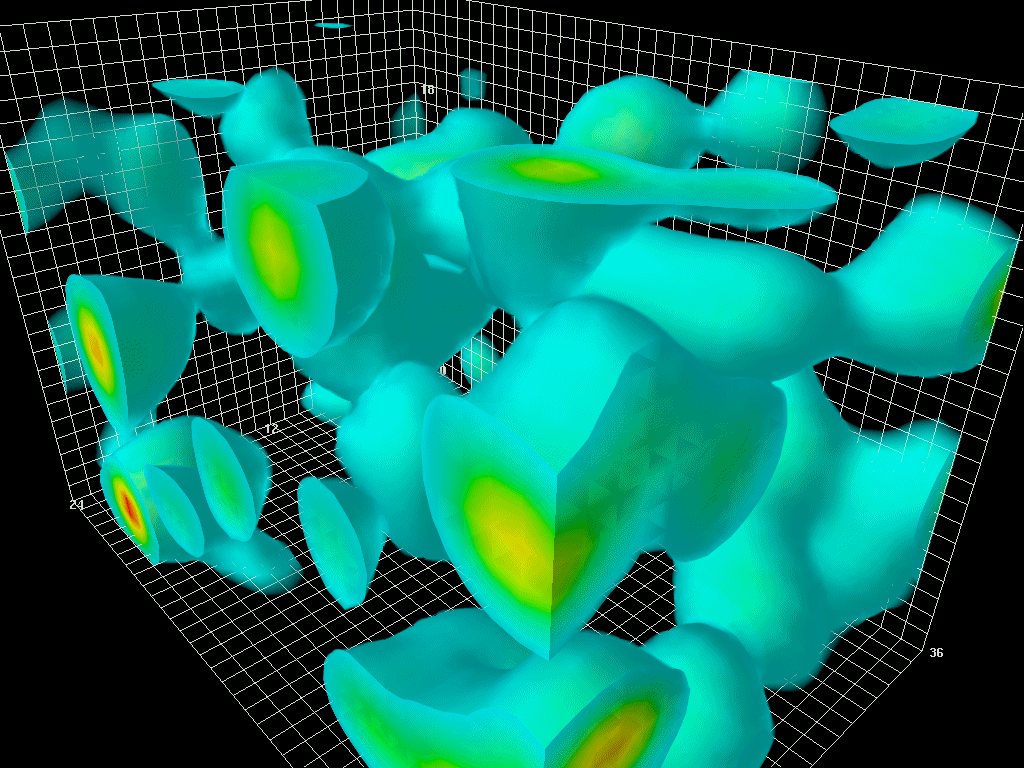
In recent years this direct approach, carried out on banks of supercomputers, has led to successful calculations of the masses of protons and neutrons. In the coming years it will revolutionize our quantitative understanding of nuclear physics over a broad front.
VI.
The puzzle Feynman thought he’d solved is still with us, though it has evolved in many ways.
The biggest change is that people have now measured the density of vacuum more precisely, and discovered that it does not vanish. It is the so-called “dark energy.” (Dark energy is essentially — up to a numerical factor — the same thing Einstein called the “cosmological constant.”) If you average it over the entire universe, you find that dark energy contributes about 70 percent of the total mass in the universe.
That sounds impressive, but for physicists the big puzzle that remains is why its density is as small as it is. For one thing, you’ll remember, it was supposed to be infinite, due to the contribution of fluctuating fields. One bit of possible progress is that now we know a way to escape that infinity. It turns out that for one class of fields — technically, the fields associated with particles called bosons — the energy density is positive infinity, while for another class of fields — those associated with particles called fermions — the energy density is negative infinity. So if the universe contains an artfully balanced mix of bosons and fermions, the infinities can cancel. Supersymmetric theories, which also have several other attractive features, achieve that cancellation.
Another thing we’ve learned is that in addition to fluctuating fields, the vacuum contains non-fluctuating fields, often called “condensates.” One such condensate is the so-called sigma condensate; another is the Higgs condensate. Those two are firmly established; there may be many others yet to be discovered. If you want to think of a familiar analogue, imagine Earth’s magnetic or gravitational field, elevated to cosmic proportions (and freed of Earth). These condensates should also weigh something. Indeed, simple estimates of their density give values far larger than that of the observed dark energy.
We’re left with an estimate of the dark energy that is finite (maybe), but poorly determined theoretically and, on the face of it, much too big. Presumably there are additional cancellations we don’t know about. The most popular idea, at present, is that the smallness of the dark energy is a kind of rare accident, which happens to occur in our particular corner of the multiverse. Though unlikely a priori, it is necessary for our existence, and therefore what we are fated to observe.
That story, I’m afraid, is not nearly so elegant as Feynman’s “There’s nothing there!” Let’s hope we can find a better one.
For anyone interested in learning more about Feynman diagrams and quantum electrodynamics, the author recommends Feynman’s book QED: The Strange Theory of Light and Matter.
This article was reprinted on Wired.com.



