A Proof About Where Symmetries Can’t Exist

High-dimensional lattices have symmetries that don’t necessarily translate into lower dimensions.
Introduction
Success for Robert Zimmer is defined differently these days. As the president of the University of Chicago since 2006, he’s made headlines for landing nine-figure financial gifts and writing op-eds in defense of campus free speech. But before Zimmer was a university president he was a mathematician. And long after he left serious research behind, the research plan he set in motion is finally paying off.
A year ago a trio of mathematicians solved what’s called Zimmer’s conjecture, which has to do with the circumstances under which geometric spaces exhibit certain kinds of symmetries. Their proof stands as one of the biggest mathematical achievements in recent years. It settles a question that emerged for Zimmer during a period of intense intellectual activity in the late 1970s and early 1980s.
“I’d say for five years I never went to sleep without thinking about this, every night, so it was pretty obsessing and it’s just great to see people [solve] it,” said Zimmer.
As a general rule, the more dimensions a geometric space has, the more symmetries it can have. You can see this with the circle, which exists on a two-dimensional plane, and a ball, which extends into three dimensions: There are more ways to rotate a ball than to rotate a circle. The ball’s extra dimensions create additional symmetries.
Zimmer’s conjecture concerns special kinds of symmetries known as higher-rank lattices. It asks if the dimension of a geometric space limits whether or not those types of symmetries apply. The authors of the new work — Aaron Brown and Sebastian Hurtado-Salazar of the University of Chicago and David Fisher of Indiana University — showed that below a certain dimension, these special symmetries can’t be found. They proved Zimmer’s conjecture true.
Their work settles one important longstanding question and opens the way to investigating many others. It also reveals something deeply intrinsic to geometric spaces. Symmetry is one of the most basic qualities to understand about such spaces. This new work says in precise fashion: These symmetries can exist in one type of space, but not in another. The achievement comes after progress on the conjecture had been stalled for decades.
“It looked like the kind of conjecture that could keep people busy for quite a while,” said Amie Wilkinson, a mathematician at the University of Chicago who earlier this year organized a conference about the new proof. “And in relatively simple fashion, they demolished the question.”
Satisfying Symmetries
Symmetry is among the first geometric concepts kids encounter in mathematics. Through hands-on manipulation, they see that it’s possible to rotate, flip and slide shapes around and end up with the shape they started with. This preservation of an object under change has a satisfying resonance — it’s a hint of a deep sense of order in the universe.
Mathematicians have their own formal language for studying symmetry. The language provides them with a concise way to think about all the different symmetries that apply to a given geometric space.
The square, for example, has eight symmetries — eight ways that it can be flipped or rotated to get back a square. By contrast, the circle can be rotated by any number of degrees; it has infinite symmetries. Mathematicians take all of the symmetries for a given geometric object, or space, and package them into a “group.”
Groups are objects of interest in their own right. They often emerge through the study of a particular geometric space, but they also appear in entirely nongeometric contexts. Sets of numbers can form groups, for example. (Consider: There’s a certain symmetry to being able to add +5 or –5 to a number.)
“A group can in principle arise as a symmetry of all sorts of things,” said Zimmer.
There are more exotic forms of symmetry than the ones we learn in elementary school. Consider, for example, the symmetries of lattices. The simplest lattice is just a two-dimensional grid. In the plane, you can shift the lattice up, down, left or right any number of squares and end up with a lattice that looks exactly like the one you started with. You could also reflect the lattice over any individual square in the grid. Spaces equipped with lattices have an infinite number of different lattice symmetries.
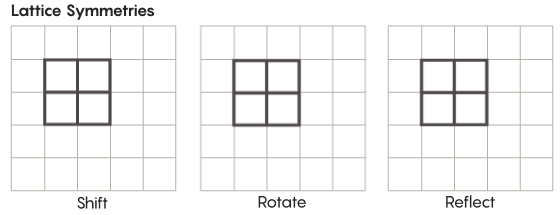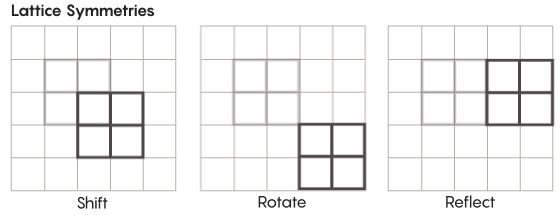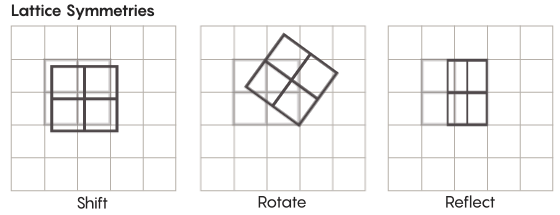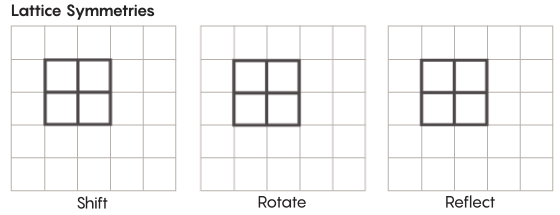
Lucy Reading-Ikkanda/Quanta Magazine
Lattices can exist in spaces of any number of dimensions. In three-dimensional space the lattice might be made of cubes instead of squares. In four dimensions and higher you can no longer picture the lattice, but it works the same way; mathematicians can precisely describe it. The groups of interest in Zimmer’s conjecture are those involving special “higher-rank” lattices, which are lattices in certain higher-dimensional spaces. “This weird grid would be very beautiful to see if you could see it, even though I can’t,” said Hurtado-Salazar. “My guess is it would be very nice to see.”
Throughout the 20th century, mathematicians discovered these groups in many different settings — not just geometry, but in number theory, logic and computer science as well. When new groups are discovered it’s natural to ask — what kinds of spaces exhibit these particular collections of symmetries?
Sometimes it’s obvious when groups can’t be applied to a space. It takes just a moment to realize that the symmetry group of the circle can’t be applied to the square. Rotate the square by 10 degrees, for example, and you don’t get back the square you started with. But the combination of a group with infinite symmetries and a space with many dimensions makes it hard to determine whether or not the group applies.
“As you get more complicated groups in much higher dimension,” said Zimmer, “these questions become much more complex.”
Loose Connections
When we think of symmetry, we picture a whole shape being rotated, like a square turned clockwise 90 degrees. At a granular level, though, symmetry is really about moving points. To transform a space by symmetry means to take each point in the space and move it to some other point in the space. In that light, rotating a square clockwise by 90 degrees really means: Take each point on the square and rotate it clockwise 90 degrees so that it ends up on a different edge from where it started.
This business of moving around points can be done in more or less rigid fashion. The most familiar symmetry transformations — reflect a square over its diagonal, or rotate the square 90 degrees — are very rigid. They’re rigid in the sense that they don’t really scramble the points. Points that were vertices before the reflection are still vertices after the reflection (just different vertices) and points that formed straight edges before the reflection still form straight edges after the reflection (just different straight edges).
There are looser, more flexible types of symmetry transformations, though, and these are the ones of interest in Zimmer’s conjecture. In these transformations, points are more thoroughly reorganized; they don’t necessarily maintain their prior relationship with one another after a transformation has been applied. For example, you could move each point on the square three units around the perimeter of the square — that satisfies the basic requirements of a symmetry transformation, that it simply move every point in the space to some new position in the space. Aaron Brown, coauthor of the new proof, described what these looser kinds of transformations could look like in the context of a ball.
“You could take the north and south poles and twist them in opposite directions. Distances and points would get pulled apart,” Brown said.
When you’re talking about a grid, instead of just shifting the grid in the plane, you’re allowed to twist the grid, or stretch it in some places and contract it in others, so that the transformed grid no longer overlays perfectly on the starting grid. These types of transformations are less rigid. They’re called diffeomorphisms.
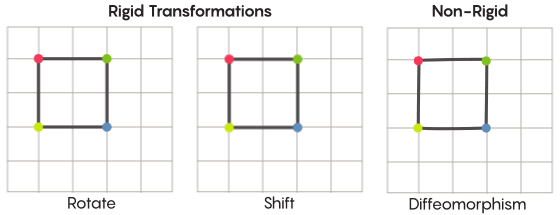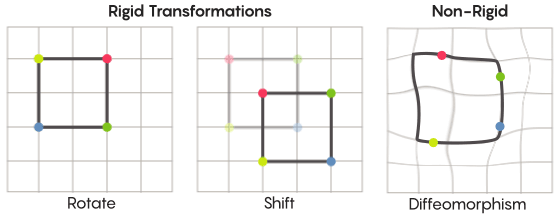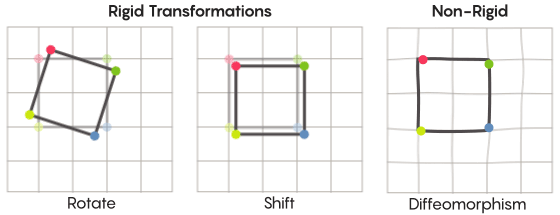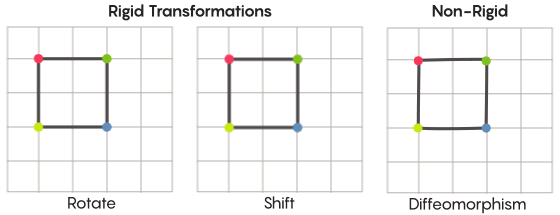
Lucy Reading-Ikkanda/Quanta Magazine
Zimmer had a good reason for using this looser version of symmetry in his conjecture. The special higher-rank lattices involved in his conjecture were first studied in the 1960s by Grigory Margulis, who won the Fields Medal for his work. Margulis gave a complete description of which kinds of spaces can be transformed by these higher-rank lattices when you permit only rigid transformations.
Zimmer’s conjecture was a natural continuation of Margulis’ work. It starts with the list of spaces on which higher-rank lattices can act — the list that Margulis found — and asks whether this list expands when you allow the lattices to act in less rigid ways.
In their new work, the three mathematicians prove that relaxing the definition of symmetry doesn’t actually change when higher-rank lattice symmetries apply. Even when you allow the lattices to transform a space in very irregular ways — by shearing, bending, stretching — the lattices are still tightly restricted in where they can act.
“Because you’ve added so much flexibility into the problem, the immediate naive intuition is of course these lattices can act. So it’s surprising that the answer is no, in some cases, they can’t,” Fisher said.
The mathematicians established exact relationships between the dimension of a space and the dimension, or rank, of the lattices that can serve as symmetries of that space. In general, they showed that the higher the rank of the lattice, the more dimensions a space needs in order to be able to accommodate it. Even when you have considerable flexibility in how you transform a space, high-rank lattice transformations are restricted to higher-dimensional spaces.
“It tells you there is something very fundamental about how [spaces] are put together that reflect whether they can have these actions,” said Wilkinson.
Zimmer’s conjecture is just a first step in a bigger program. By answering the conjecture, the coauthors of the new work have placed a rough-cut restriction on the spaces in which higher-rank lattices can act. The next and even more ambitious phase of work is to focus on just those spaces in which the lattices do appear — and then to classify all the different ways in which those lattices transform those spaces.
“The program ultimately should be able to classify all these ways. There are a lot of interesting questions well beyond what you see in establishing that there are certain places the lattices just can’t act,” said Zimmer.