Bubble Experiment Finds Universal Laws
All droplet formation was once thought to be universal.
Xiangdong Shi and Sidney Nagel
Introduction
Each time a drop drips from a faucet, nature performs a magic trick. Breaking one blob into two calls for passage through a singularity — a single point where physical quantities flirt with the infinite. As the neck connecting the two blobs thins to nothing, the fluid pressure and speed race upward toward infinity, as if they were being divided by zero. Here, the equations used to describe fluids suffer a mathematical explosion. Order returns only after the sudden break.
Years ago, physicists studying the phenomenon realized that this messy, violent process brings about a hidden regularity: Every drop in the world has one of just a few characteristic neck shapes. Factors like gravity, faucet design and a drafty kitchen may have started the dripping, but all that matters in the end is the straightforward struggle between the squeeze of surface tension and the resistance of the neck’s inertia. “The point of breakup would have looked the same,” wrote Sidney Nagel, a physicist at the University of Chicago, “even if it had been formed from a wave tossed into the air at the shores of Lake Michigan.”
Droplets became a prime example of “universality,” which describes events that play out exactly the same way time and again, even across different materials and under substantially different conditions. Universality’s predictability can be used to explain the large-scale behavior of messy, changing systems that first-principle mathematical models can’t always analyze thoroughly, such as cracking surfaces. Universality allows researchers to describe these events without worrying about the nitty-gritty molecular or atomic details. “Universality is a ubiquitous idea that helps us simplify complex systems,” said Justin Burton, a soft-matter physicist at Emory University.
A recent study has identified universality in a new system: bubbles trapped in a narrow tube. The work comes as something of a surprise, since bubbles historically were the system that taught physicists the limits of universality. Now researchers have a way to turn that universality on and off.
Ultimately, the hope is that studying singularities and universality in relatively straightforward systems such as bubbles can provide insight into what goes on in the less camera-friendly corners of the cosmos. “Droplets and bubbles, we see them on a daily basis,” said Amir Pahlavan, a mechanical engineer at Princeton University and a co-author of the recent work. “For black holes, it’s much harder to study and observe them.”
The End of Universality
Early pioneers of universality, led by the physicist Leo Kadanoff, discovered that systems as different as avalanching sand piles and magnetizing metals all operate on multiple scales. At a tipping point, large avalanches can occur alongside small ones. The tendency for the large to mingle only with the large, and the small only with the small, melts away, and effects from one level bleed smoothly into the next.
Spurred in part by Kadanoff’s work, physicists in the early 1990s demonstrated, first theoretically and then experimentally, that droplet formation is a universal phenomenon.
For years researchers had assumed that only a molecular theory could fully describe the breakup, since the description of the smooth fluid, known as the Navier-Stokes equations, fails when the pressure and velocity explode. With universality guaranteeing uniform shapes before and after pinch-off, however, Jens Eggers, a physicist and mathematician now at the University of Bristol, found a way to extend the fluid mathematics across the singularity, ignoring the molecules themselves.
These developments set off a flood of research using setups with different numbers of liquids and fluids with varying consistencies. Tweaking these apparatuses lets physicists study unexplained aspects of fluid dynamics and explore the limits of universality by accessing different “universality classes,” each defined by its own characteristic number.
One major surprise came when Nagel and his colleagues in Chicago reversed the falling-drop experiment. They swapped a water droplet falling through air for an air bubble rising through a fluid.
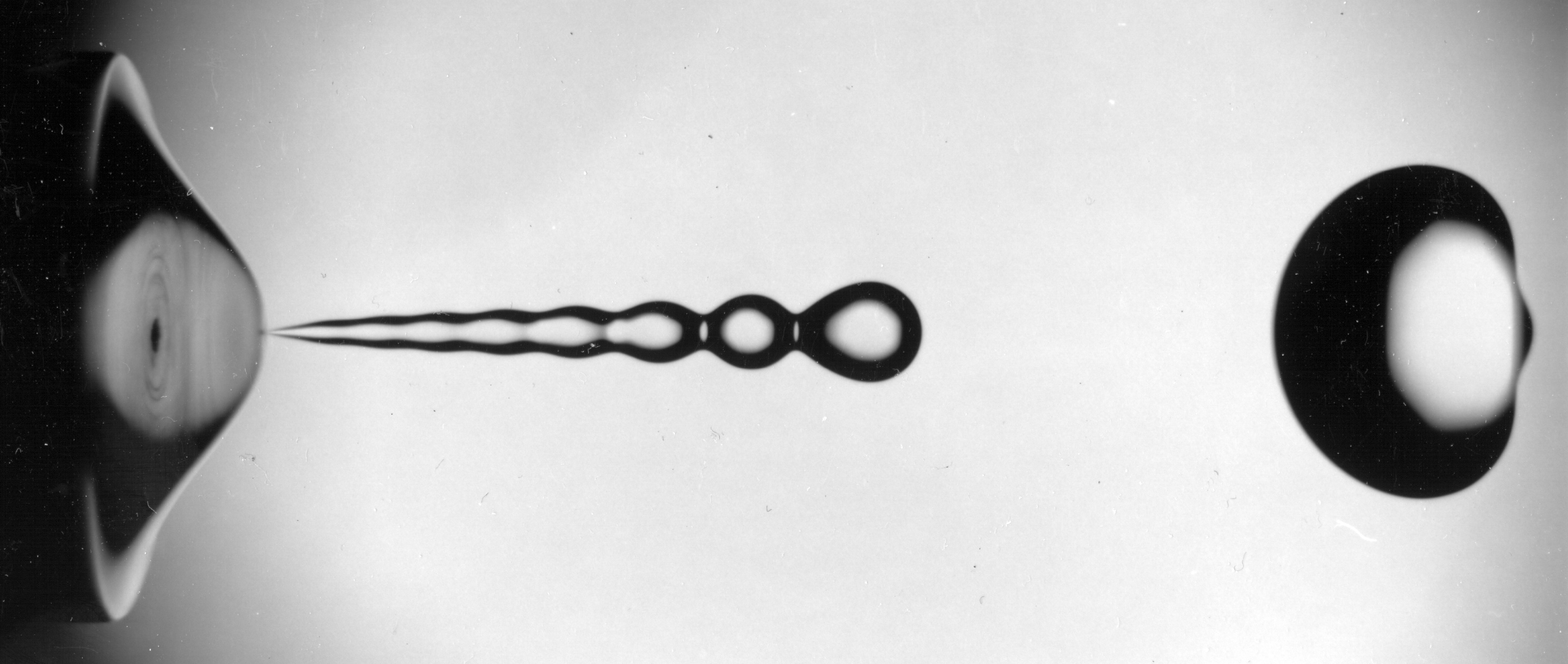
Guided by insights gained from thinning drops, the graduate student heading up the project tried photographing the dividing bubbles from every angle, searching for some universal way in which every event plays out identically. Yet each pinch-off looked different, with initial ripples in the surrounding water or central air stream surviving all the way to the singularity and wrecking the neck’s Platonic symmetry.
Eventually, the team had to conclude that bubble breakup is not universal. Unlike droplets, the final bubble assumes a shape that maintains a “memory” of the conditions under which it was born. The drive to extend universality was stopped by a pocket of air. “If you believe what experiment tells you without being blinded by what you’re told,” Nagel said, “you’ll see that nature has other plans in mind.”
The new study has revealed a way to get universality back into the bubbles. The work started when Pahlavan, at the time a member of Ruben Juanes’ lab at the Massachusetts Institute of Technology, was working on a project that involved pushing air through tubes less than 1 millimeter wide. He noticed that the equations describing bubbles suggested the neck should pass through two distinct phases as it approached the point of pinch-off. One phase would be identical to the profile seen in the Chicago team’s early work, and the other would be entirely new.
When he viewed the breakup in extreme slow motion, Pahlavan found that at 1 second before breakup, the shape of the bubble neck was self-similar: After zooming in on a section of the curve, he found that the new curve could be stretched to look the same as it did at the larger scale. (Fractal-like self-similarity is a common feature of universal systems because it relates to the notion that the system lacks a special scale.) One millisecond before breakup, however, the type of stretching needed to map an up-close view onto the original curve changed — an indication that the neck had switched into a different regime of self-similarity.

Bubbles in a tube smaller than a millimeter wide appear to retain no “memory” of the details that led to the break.
Amir Pahlavan
The new first stage acted universal, wiping the system’s “memory” of details like the nozzle size. The second stage matched the Chicago team’s results, which were not universal. But by the time the second stage arrived, there were no details left to remember, so the overall system behaved universally.
Pahlavan tweaked the bubble experiment in a dozen ways, varying the tube size and liquid consistency, but each and every breakup played out the same way.
The new work proves that systems can switch universality on and off, and that sticking them in a container is one way to make them do so. “What this paper shows nicely is a way that you can restore [universality] by applying some confinement,” Burton said.
“Singularity formation is interesting because you’re finding universality classes and talking about things that are insensitive [to the initial details],” said Pahlavan, “so they should be more general than the problem you’re studying.”
Which means, for instance, that they can be used to better understand black holes.
Cosmic Singularities
Try as you might, you’ll never split a black hole in our universe. But theorists playing around in higher dimensions have discovered that the objects’ theoretical cousins in five dimensions or higher — dubbed “black strings” for their cylindrical appearance in the extra dimensions — would lead more precarious lives.
Could these enigmatic objects collapse and split into two? General relativity in five dimensions is too hard to solve exactly, but in 2010, the physicists Luis Lehner and Franz Pretorius used a computer model to compute the fate of a black string.
The simulation spit out a video that felt surprisingly familiar, Pretorius said. It looked just like a fluid stream breaking into drops: A large bead formed, leaving behind a thinner stream that, in turn, bulged into smaller drops connected by even thinner streams, and so on. Fluid behavior suggests that the strings should eventually snap into spherical black hole droplets. But without a particulate theory of quantum gravity, the simulation crashes as it approaches the pinch-off point.
Black-string breakup hasn’t been proved to be a universal process (although Pretorius said simulations hint that it should be), but if it is, he speculates, perhaps theorists can ignore the quantum details of gravity just as physicists managed to sidestep the molecular details of drop formation. “We might be able to figure out what happens before and after breakup purely from classical general relativity,” he said.
As the neck evolution gets close to the breakup point, the theoretical objects might even have something interesting to say about quantum gravity itself, Pretorius suggests.
Beyond theoretical black strings, the universe is awash in entities experiencing singular breakups. Binary stars can form when a spinning gas cloud gradually divides in half, and the splitting of the atom during nuclear fission can also be treated as a liquid. Different forces drive these events so their mathematical descriptions vary, and as the Chicago team learned, not all singularities will necessarily be universal. But by studying drops and bubbles, physicists have built a toolkit of general problem-solving strategies that can help them tackle other sorts of singularities.
Continuing to wring additional drops of insight from singularities that can be observed in the lab will expand those techniques. “From the Big Bang — that’s kind of the all-time original singularity — to the breakup of a bubble, these things keep popping up everywhere,” Burton said. “Really trying to understand the basic physics of them is an important challenge.”




