Geometers Engineer New Tools to Wrangle Spacecraft Orbits
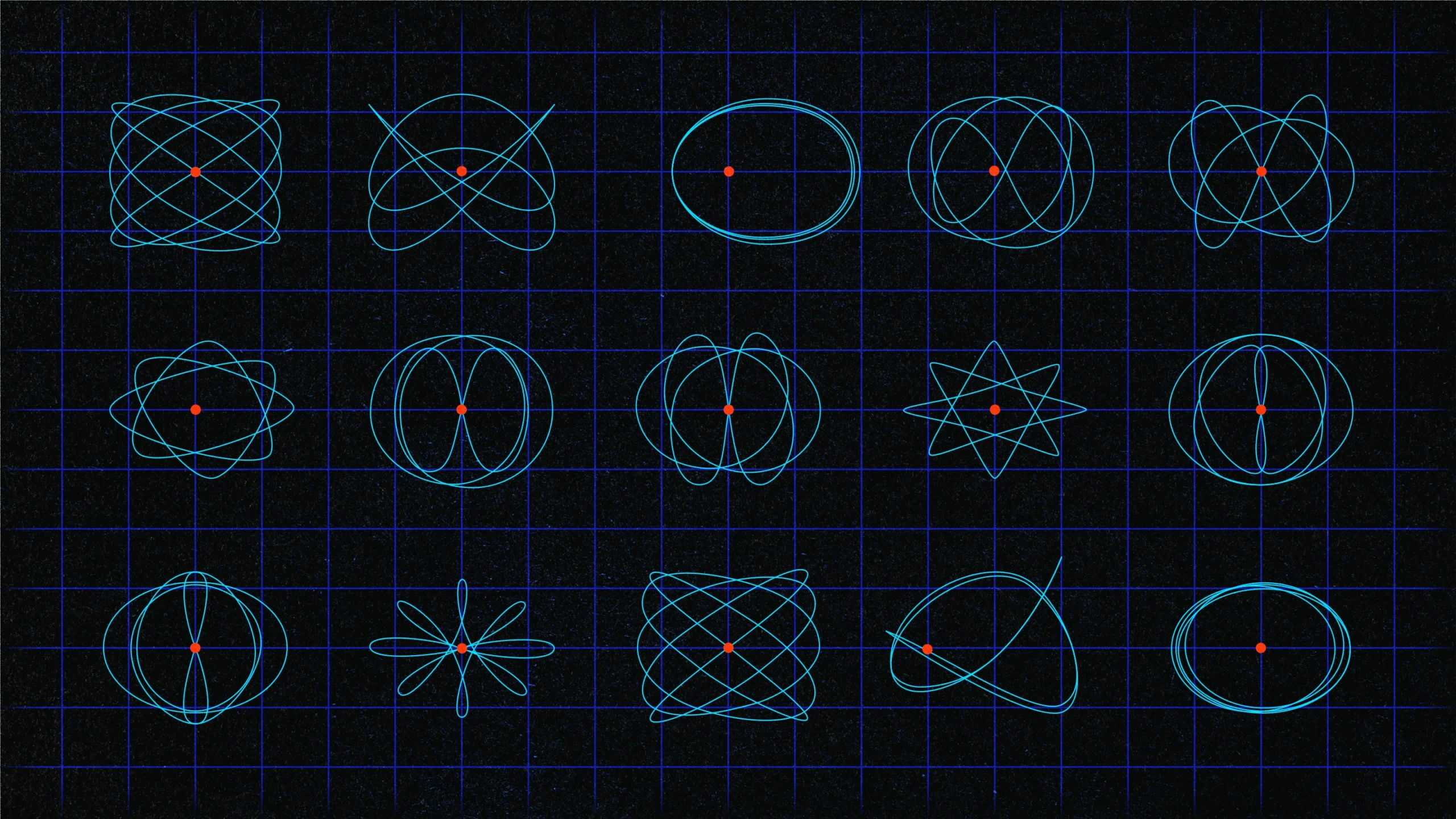
These periodic orbits around a model of the Jupiter-Europa system show the varied and intricate possibilities that mission planners must knit together.
Kristina Armitage/Quanta Magazine
Introduction
In October, a Falcon Heavy rocket is scheduled to launch from Cape Canaveral in Florida, carrying NASA’s Europa Clipper mission. The $5 billion mission is designed to find out if Europa, Jupiter’s fourth-largest moon, can support life. But because Europa is constantly bombarded by intense radiation created by Jupiter’s magnetic field, the Clipper spacecraft can’t orbit the moon itself. Instead, it will slide into an eccentric orbit around Jupiter and gather data by repeatedly swinging by Europa — 53 times in total — before retreating from the worst of the radiation. Every time the spacecraft rounds Jupiter, its path will be slightly different, ensuring that it can take pictures and gather data from Europa’s poles to its equator.
To plan convoluted tours like this one, trajectory planners use computer models that meticulously calculate the trajectory one step at a time. The planning takes hundreds of mission requirements into account, and it’s bolstered by decades of mathematical research into orbits and how to join them into complicated tours. Mathematicians are now developing tools which they hope can be used to create a more systematic understanding of how orbits relate to one another.
“What we have is the previous computations that we’ve done, that guide us as we do the current computations. But it’s not a complete picture of all the options that we have,” said Daniel Scheeres, an aerospace engineer at the University of Colorado, Boulder.
“I think that was my biggest frustration when I was a student,” said Dayung Koh, an engineer at NASA’s Jet Propulsion Laboratory. “I know these orbits are there, but I don’t know why.” Given the expense and complexity of missions to the moons of Jupiter and Saturn, not knowing why orbits are where they are is a problem. What if there is a completely different orbit that could get the job done with fewer resources? As Koh said: “Did I find them all? Are there more? I can’t tell that.”
After getting her doctorate from the University of Southern California in 2016, Koh grew interested in how orbits can be cataloged into families. Jovian orbits that are far from Europa form such a family; so do orbits close to Europa. But other families are less obvious. For instance, for any two bodies, like Jupiter and Europa, there is an intermediate point where the two bodies’ gravitational effects balance to create stable points. Spacecraft can orbit this point, even though there is nothing at the center of the orbit. These orbits form a family called Lyapunov orbits. Add a little energy to such an orbit by firing a spacecraft engine, and at first you’ll stay in the same family. But add enough, and you’ll cross over into another family — say, one that includes Jupiter inside its orbits. Some orbit families might require less fuel than others, remain in sunlight at all times, or have other useful features.
In 2021, Koh came across a paper that discussed how to grapple with chaotic orbits from the perspective of symplectic geometry, an abstract field of math that is generally far removed from messy real-world details. She started to suspect that symplectic geometry might have the tools she needed to better understand orbits, and she got in touch with Agustin Moreno, the author of the paper. Moreno, then a postdoctoral fellow at Uppsala University in Sweden, was surprised and pleased to hear that someone at NASA was interested in his work. “It was unexpected, but it was also quite interesting and sort of motivating at the same time,” he said.
The two began working together, seeking to apply Moreno’s abstract techniques to the Jupiter-Europa system and to Saturn and its moon Enceladus, which, like Europa, might have life in its underground ocean. In the past year, together with other collaborators, they have written a series of papers that create a framework for cataloging orbits. In January, Moreno, now a professor at Heidelberg University, completed an early draft that turned his survey paper into a book on the subject. With the book, he wants to make the abstract field of symplectic geometry useful to engineers who are trying to plan space missions. If he succeeds, he will be reuniting fields of inquiry that have grown apart over the centuries.
No Royal Road to Geometry
Symplectic geometry has its roots in physics. To take a simple example, imagine a pendulum. Its motion can be described by two parameters: angle and speed. If the speed is low enough, the pendulum will oscillate back and forth. If the speed is higher, it will spin around in a circle. In an idealized pendulum without friction, once you’ve chosen a starting angle and speed, the system’s behavior is determined for all time.
Merrill Sherman/Quanta Magazine
Merrill Sherman/Quanta Magazine
You can create a graph with the angle as the x-axis and the speed as the y-axis. But since traveling 360 degrees brings you back to the start, you can sew together the vertical lines where x is zero degrees and where x is 360 degrees. This makes a cylinder. The cylinder doesn’t directly reflect physical reality — it isn’t showing paths that the pendulum traces — rather, each point on it represents a particular state of the pendulum. The cylinder, along with the laws that determine the paths the pendulum can follow, forms a symplectic space.
Since the early 17th century, when Johannes Kepler formulated his laws, physicists and mathematicians have had a firm grasp on how to describe the motion of two bodies subject to gravity. Depending on how fast they are moving, their paths form an ellipse, parabola or hyperbola. The corresponding symplectic spaces are more complicated than the one for a pendulum, but still tractable. But introducing a third object makes exact, analytic solutions impossible to calculate. And it only gets more complicated if you add more bodies to the model. “Without that analytic insight, you’re almost always, at some level, shooting into the dark,” Scheeres said.
A spacecraft that can move freely in any direction — right to left, up and down, and front to back — needs three coordinates to describe its position, and three more to describe its velocity. That makes a six-dimensional symplectic space. To describe the motion of three bodies, like Jupiter, Europa and a spacecraft, you need 18 dimensions: six per body. The geometry of the space is defined not only by the number of dimensions it has, but also by the curves that show how the physical system being described evolves over time.
Moreno and Koh worked on a “restricted” version of the three-body problem where one of the bodies (the spacecraft) is so small that it has no impact on the other two (Jupiter and Europa). To simplify things further, the researchers assumed the moon’s orbit was perfectly circular. You can take its circular orbit as a steady background against which to consider the space probe’s path. The symplectic space only has to account for the spacecraft’s position and velocity, since Jupiter and Europa’s motion can be easily described. So instead of being 18-dimensional, the corresponding symplectic space is six-dimensional. When a path in this six-dimensional space forms a loop, it represents a periodic orbit of the spacecraft through the planet-moon system.
When Koh contacted Moreno, she was curious about cases where adding just a tiny bit of energy causes a spacecraft’s orbit to jump from one family to another. These meeting points between families of orbits are called bifurcation points. Often many families will meet at a single point. This makes them particularly useful to trajectory planners. “Understanding the bifurcation structure gives you a roadmap as to where are there interesting trajectories that you should look at,” Scheeres said. Koh wanted to know how to identify and predict bifurcation points.
After hearing from Koh, Moreno enlisted a few other geometers: Urs Frauenfelder of the University of Augsburg, Cengiz Aydin of Heidelberg University, and Otto van Koert of Seoul National University. Frauenfelder and van Koert had long studied the three-body problem using symplectic geometry, even uncovering a potential new family of orbits. But though engineers planning spacecraft missions have used a myriad of mathematical tools, in recent decades they’ve been daunted by the increasing abstraction of symplectic geometry.
Throughout the following months, the engineer and the four mathematicians slowly learned about one another’s fields. “It takes a while when you’re doing interdisciplinary work to, let’s say, get over the language barriers,” Moreno said. “But after you’ve done the patient work, it starts paying off.”
The Toolkit
The team put together a number of tools which they hope will be useful to mission planners. One of the tools is a number called the Conley-Zehnder index that can help determine when two orbits belong to the same family. To calculate it, researchers examine points that are close to — but not on — the orbit they want to study. Imagine, for instance, that a spacecraft is following an elliptical orbit around Jupiter, influenced by gravity from Europa. If you nudge it off its path, its new trajectory will imitate the original orbit, but only crudely. The new path will spiral around the original orbit, coming back to a slightly different point after it circles Jupiter. The Conley-Zehnder index is a measurement of just how much spiraling goes on.
Surprisingly, the Conley-Zehnder index doesn’t depend on the specifics of how you nudge the spacecraft — it’s a number associated with the entire orbit. What’s more, it’s the same for all orbits in the same family. If you compute the Conley-Zehnder index for two orbits, and you get two different numbers, you can be sure that the orbits are from different families.
Another tool, called the Floer number, can hint at undiscovered families of orbits. Suppose several families collide at a bifurcation point when the energy hits a particular number, and several more families branch out from that bifurcation point when the energy is higher. This forms a web of families whose central hub is the bifurcation.
You can calculate the Floer number associated with this bifurcation point as a simple function of the Conley-Zehnder indexes associated with each relevant family. You can compute this function both for all the families that have energy just a bit smaller than the bifurcation point and for families whose energy is larger. If the two Floer numbers differ, that’s a clue that there are hidden families linked to your bifurcation point.
“What we’re doing is providing tools against which engineers test their algorithms,” Moreno said. The new tools are primarily designed to help engineers understand how families of orbits fit together and to prod them to look for new families where warranted; it’s not meant to substitute for the trajectory-finding techniques that have been honed over decades.
In 2023, Moreno presented the work to a conference organized by the “Space Flight Mechanics Committee,” and he has been in contact with engineers who research space trajectories, including some at JPL and Scheeres’ lab at Boulder. Scheeres welcomed the intermingling of fields: He had long known about the symplectic approach to planetary motion, but felt out of his depth mathematically. “It was really exciting to see the mathematicians trying to bring their expertise down into the engineering side,” he said. Scheeres’ group is now working on a more complex system involving four bodies.
Ed Belbruno, a trajectory planning consultant (and former JPL orbital analyst) who has worked with Frauenfelder, cautions that the applications are not direct. “Although a mathematical technique such as symplectic geometry can come up with trajectories which are really cool, and you get a whole slew of them, it may be that very, very few, if any, satisfy the constraint” that a real mission might need, he said.
Though the Clipper trajectories are already largely settled, Moreno is looking to the next planet: Saturn. He has already presented his research to mission planners at JPL who hope to send a spacecraft to Saturn’s moon Enceladus. Moreno hopes that symplectic geometry will “become part of the standard space mission toolkit.”



