How Claude Shannon Invented the Future

Estate of Francis Bello / Science Source
Introduction
Science seeks the basic laws of nature. Mathematics searches for new theorems to build upon the old. Engineering builds systems to solve human needs. The three disciplines are interdependent but distinct. Very rarely does one individual simultaneously make central contributions to all three — but Claude Shannon was a rare individual.
Despite being the subject of the recent documentary The Bit Player — and someone whose work and research philosophy have inspired my own career — Shannon is not exactly a household name. He never won a Nobel Prize, and he wasn’t a celebrity like Albert Einstein or Richard Feynman, either before or after his death in 2001. But more than 70 years ago, in a single groundbreaking paper, he laid the foundation for the entire communication infrastructure underlying the modern information age.
Shannon was born in Gaylord, Michigan, in 1916, the son of a local businessman and a teacher. After graduating from the University of Michigan with degrees in electrical engineering and mathematics, he wrote a master’s thesis at the Massachusetts Institute of Technology that applied a mathematical discipline called Boolean algebra to the analysis and synthesis of switching circuits. It was a transformative work, turning circuit design from an art into a science, and is now considered to have been the starting point of digital circuit design.
Next, Shannon set his sights on an even bigger target: communication.
Communication is one of the most basic human needs. From smoke signals to carrier pigeons to the telephone to television, humans have always sought methods that would allow them to communicate farther, faster and more reliably. But the engineering of communication systems was always tied to the specific source and physical medium. Shannon instead asked, “Is there a grand unified theory for communication?” In a 1939 letter to his mentor, Vannevar Bush, Shannon outlined some of his initial ideas on “fundamental properties of general systems for the transmission of intelligence.” After working on the problem for a decade, Shannon finally published his masterpiece in 1948: “A Mathematical Theory of Communication.”
The heart of his theory is a simple but very general model of communication: A transmitter encodes information into a signal, which is corrupted by noise and then decoded by the receiver. Despite its simplicity, Shannon’s model incorporates two key insights: isolating the information and noise sources from the communication system to be designed, and modeling both of these sources probabilistically. He imagined the information source generating one of many possible messages to communicate, each of which had a certain probability. The probabilistic noise added further randomness for the receiver to disentangle.
Before Shannon, the problem of communication was primarily viewed as a deterministic signal-reconstruction problem: how to transform a received signal, distorted by the physical medium, to reconstruct the original as accurately as possible. Shannon’s genius lay in his observation that the key to communication is uncertainty. After all, if you knew ahead of time what I would say to you in this column, what would be the point of writing it?
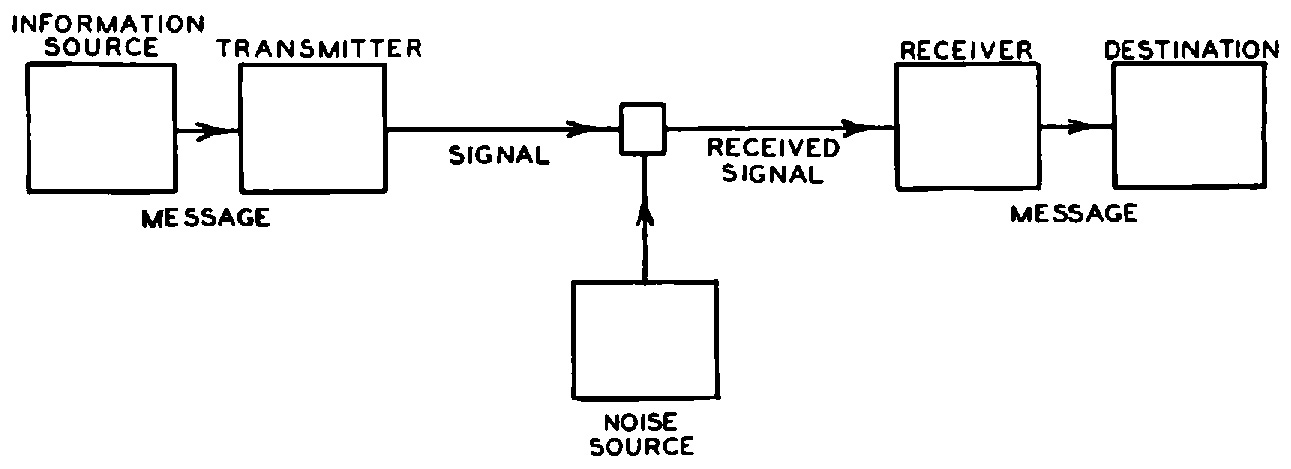
A schematic diagram of Shannon’s model of communication, as taken from his paper.
This single observation shifted the communication problem from the physical to the abstract, allowing Shannon to model the uncertainty using probability. This came as a total shock to the communication engineers of the day.
Given that framework of uncertainty and probability, Shannon set out in his landmark paper to systematically determine the fundamental limit of communication. His answer came in three parts. Playing a central role in all three is the concept of an information “bit,” used by Shannon as the basic unit of uncertainty. A portmanteau of “binary digit,” a bit could be either a 1 or a 0, and Shannon’s paper is the first to use the word (though he said the mathematician John Tukey used it in a memo first).
First, Shannon came up with a formula for the minimum number of bits per second to represent the information, a number he called its entropy rate, H. This number quantifies the uncertainty involved in determining which message the source will generate. The lower the entropy rate, the less the uncertainty, and thus the easier it is to compress the message into something shorter. For example, texting at the rate of 100 English letters per minute means sending one out of 26100 possible messages every minute, each represented by a sequence of 100 letters. One could encode all these possibilities into 470 bits, since 2470 ≈ 26100. If the sequences were equally likely, then Shannon’s formula would say that the entropy rate is indeed 470 bits per minute. In reality, some sequences are much more likely than others, and the entropy rate is much lower, allowing for greater compression.
Second, he provided a formula for the maximum number of bits per second that can be reliably communicated in the face of noise, which he called the system’s capacity, C. This is the maximum rate at which the receiver can resolve the message’s uncertainty, effectively making it the speed limit for communication.
Finally, he showed that reliable communication of the information from the source in the face of noise is possible if and only if H < C. Thus, information is like water: If the flow rate is less than the capacity of the pipe, then the stream gets through reliably.
While this is a theory of communication, it is, at the same time, a theory of how information is produced and transferred — an information theory. Thus Shannon is now considered “the father of information theory.”
His theorems led to some counterintuitive conclusions. Suppose you are talking in a very noisy place. What’s the best way of making sure your message gets through? Maybe repeating it many times? That’s certainly anyone’s first instinct in a loud restaurant, but it turns out that’s not very efficient. Sure, the more times you repeat yourself, the more reliable the communication is. But you’ve sacrificed speed for reliability. Shannon showed us we can do far better. Repeating a message is an example of using a code to transmit a message, and by using different and more sophisticated codes, one can communicate fast — all the way up to the speed limit, C — while maintaining any given degree of reliability.
Another unexpected conclusion stemming from Shannon’s theory is that whatever the nature of the information — be it a Shakespeare sonnet, a recording of Beethoven’s Fifth Symphony or a Kurosawa movie — it is always most efficient to encode it into bits before transmitting it. So in a radio system, for example, even though both the initial sound and the electromagnetic signal sent over the air are analog wave forms, Shannon’s theorems imply that it is optimal to first digitize the sound wave into bits, and then map those bits into the electromagnetic wave. This surprising result is a cornerstone of the modern digital information age, where the bit reigns supreme as the universal currency of information.
Shannon’s general theory of communication is so natural that it’s as if he discovered the universe’s laws of communication, rather than inventing them. His theory is as fundamental as the physical laws of nature. In that sense, he was a scientist.
Shannon invented new mathematics to describe the laws of communication. He introduced new ideas, like the entropy rate of a probabilistic model, which have been applied in far-ranging branches of mathematics such as ergodic theory, the study of long-term behavior of dynamical systems. In that sense, Shannon was a mathematician.
But most of all, Shannon was an engineer. His theory was motivated by practical engineering problems. And while it was esoteric to the engineers of his day, Shannon’s theory has now become the standard framework underlying all modern-day communication systems: optical, underwater, even interplanetary. Personally, I have been fortunate to be part of a worldwide effort to apply and broaden Shannon’s theory to wireless communication, increasing communication speed by two orders of magnitude over multiple generations of standards. Indeed, the 5G standard currently rolling out uses not one but two practical codes proved to achieve Shannon’s speed limit.


Although Shannon died in 2001, his legacy lives on in the technology that makes up our modern world and in the devices he created, like this remote-controlled bus.
Courtesy of MIT Museum
Shannon figured out the foundation for all this more than 70 years ago. How did he do it? By focusing relentlessly on the essential feature of a problem while ignoring all other aspects. The simplicity of his model of communication is a good illustration of this style. He also knew to focus on what is possible, rather than what is immediately practical.
Shannon’s work illustrates the true role of top-rate science. When I started graduate school, my adviser told me that the best work would prune the tree of knowledge, rather than grow it. I didn’t know what to make of this message then; I always thought my job as a researcher was to add my own twigs. But over my career, as I had the opportunity to apply this philosophy in my own work, I began to understand.
When Shannon began studying communication, engineers already had a large collection of techniques. It was his unifying work that pruned all these twigs of knowledge into a single coherent and lovely tree — one that’s borne fruit for generations of scientists, mathematicians and engineers.
Correction: January 4, 2021
An earlier version of this article incorrectly stated the rate of text messages possible if sending 100 letters per minute. It is one of 26100 messages every minute, not 26100.



