Mathematicians Discover New Shapes to Solve Decades-Old Geometry Problem
Introduction
In 1986, after the space shuttle Challenger exploded 73 seconds into its flight, the eminent physicist Richard Feynman was called in to find out what had gone wrong. He later demonstrated that the “O-ring” seals, which were meant to join sections of the shuttle’s solid rocket boosters, had failed due to cold temperatures, with catastrophic results. But he also discovered more than a few other missteps.
Among them was the way NASA had calculated the O-rings’ shape. During preflight testing, the agency’s engineers had repeatedly measured the width of the seals to verify that they had not become distorted. They reasoned that if an O-ring had been slightly squashed — had become, say, an oval, instead of maintaining its circular shape — then it would no longer have the same diameter all the way around.
These measurements, Feynman later wrote, were useless. Even if the engineers had taken an infinite number of measurements and found the diameter to be exactly the same each time, there are many “bodies of constant width,” as these shapes are called. Only one is a circle.
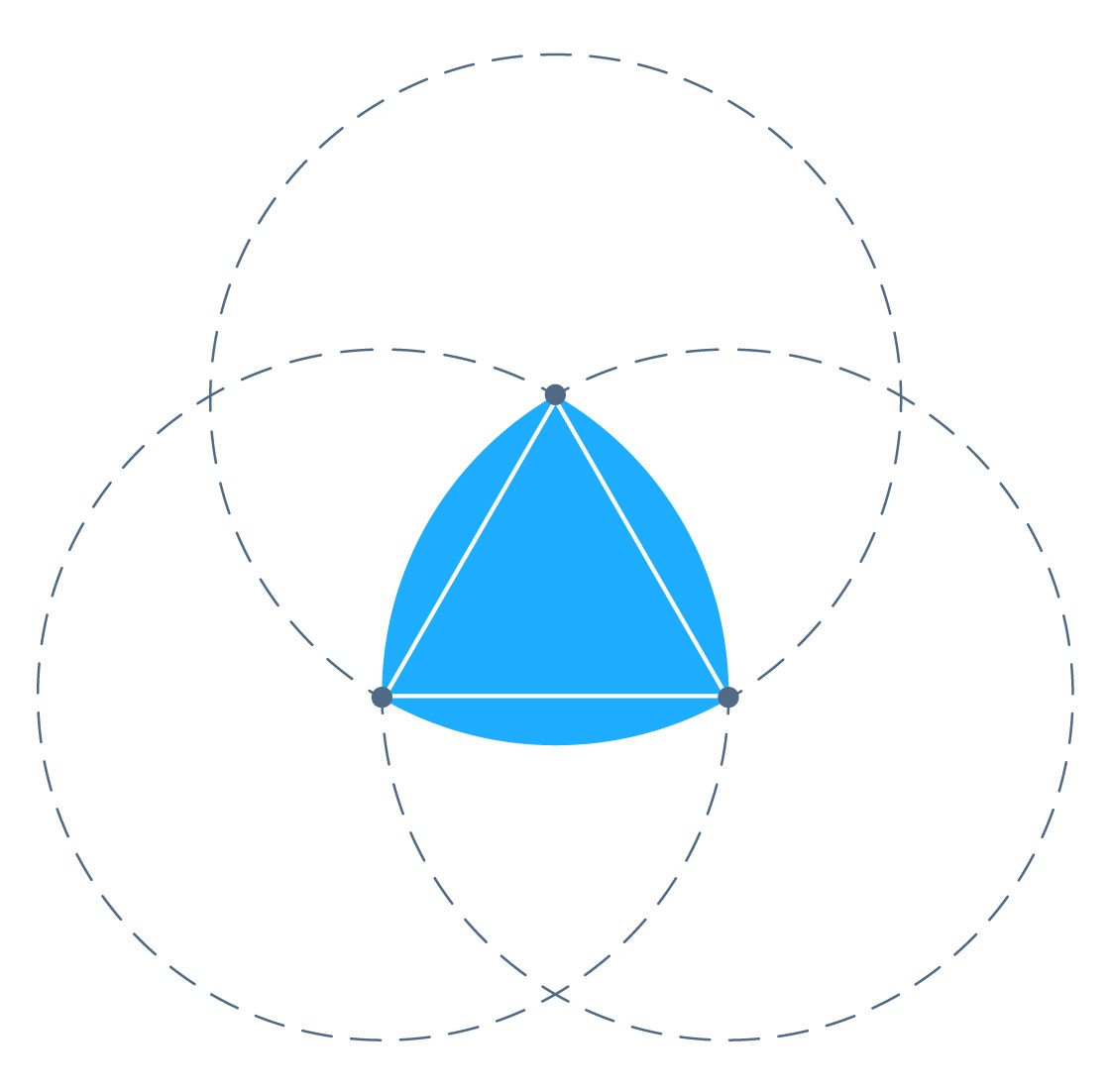
Arguably the best known noncircular body of constant width is the Reuleaux triangle, which you can construct by taking the central region of overlap in a three-circle Venn diagram. For a given width in two dimensions, a Reuleaux triangle is the constant-width shape with the smallest possible area. A circle has the largest.
In three dimensions, the largest body of constant width is a ball. In higher dimensions, it’s simply a higher-dimensional ball — the shape swept out if you hold a needle at a point and let it rotate freely in every direction.
But mathematicians have long wondered if it’s always possible to find smaller constant-width shapes in higher dimensions. Such shapes exist in three dimensions: Though these Reuleaux-like blobs might look a bit pointy, sandwich them between two parallel planes and they will roll smoothly, like a ball. But it’s much harder to tell whether this is true in general. It could be that in higher dimensions, the ball is optimal. And so in 1988, Oded Schramm, then a graduate student at Princeton University, asked a simple-sounding question: Can you construct a constant-width body in any dimension that is exponentially smaller than the ball?
Now, in a paper posted online in May, five researchers — four of whom grew up in Ukraine and have known each other since their high school or college days — have reported that the answer is yes.
The result not only solves a decades-old problem, but gives mathematicians their first glimpse into what these mysterious higher-dimensional shapes might look like. Although these shapes are easy to define, they’re surprisingly mysterious, said Shiri Artstein, a mathematician at Tel Aviv University who wasn’t involved in the work. “Any new thing we learn about them, any new construction or computation, is at this point interesting.” Now researchers can finally access a corner of the geometric universe that was once completely unapproachable.
Planting the Seed
Andrii Arman and Danylo Radchenko met in the mid-2000s at a math-focused high school in Kyiv and were also teammates on Ukraine’s competitive Math Olympiad squad. They became friends, but didn’t stay in close touch. When their mathematical work later pulled them independently into the orbits of both Andriy Prymak and Andrii Bondarenko — who had attended Kyiv National University together in the 1990s — they reconnected. The four mathematicians have since moved to different cities around the world and pursued different research programs, but they gather twice a week over Zoom to work together on tough geometric proofs.

With their collaborators, Andrii Bondarenko (left) and Danylo Radchenko recently proved that you can always find small shapes of constant width in high dimensions.
From left: Ekaterina Poliakova/Norwegion University of Science and Technology; Grégory Hau
Constant-width shapes were not initially on the agenda. Last year, the group was instead trying to answer a related question called the Borsuk problem, which had stumped prominent mathematicians for over a century. But an idea kept popping up during their meetings: When Schramm posed his question about constant-width bodies in the 1980s, he also suggested that understanding such shapes might provide a way to tackle the Borsuk problem.
The Ukrainian mathematicians had been pursuing a different approach, and some of them were reluctant to change focus. But Bondarenko, now at the Norwegian University of Science and Technology, insisted that they try, even if it didn’t help them directly. “He was always emphasizing that the problem is important in its own right,” said Arman, who is currently a postdoctoral researcher at the University of Manitoba. Eventually, the rest of the team agreed to make the attempt.
To understand what they did, it helps to think back to the Reuleaux triangle in two dimensions. Say you want to build a Reuleaux triangle of a given width. First draw an equilateral triangle — what the mathematicians call a seed. Choose a point on the triangle’s boundary and draw a circle around it with a radius equal to the width you want the final shape to be. Now do this at every point on the triangle’s boundary, so that you get a set of infinitely many circles.
Look at the region where those circles overlap. Somewhere within it, you’ll be able to find a body of constant width — you just have to figure out which subset of your seed you actually need. In this case, you can look at just the three vertices of the equilateral triangle, rather than all the points on its boundary. Draw circles around those three points, and you’ll get a Venn diagram; its overlapping region is the Reuleaux triangle.
Mark Belan for Quanta Magazine
In higher dimensions, it’s possible to use the same approach. Start with a set of points: your seed. Draw a ball around each point, take their intersection, and look for the body of constant width that lives inside that new space. But it’s much harder in high dimensions to figure out what subset of your seed will give you the shape you want.
Arman, Bondarenko, Prymak and Radchenko experimented with different seeds and eventually came up with a particular curve they wanted to use. They knew that this curve would give them a region that contained a sufficiently small body of constant width. But they wanted to understand what the constant-width body itself would look like. As they searched for an answer, Arman came across a post from 2022 on the question-and-answer site MathOverflow. The poster, Fedor Nazarov of Kent State University, had been independently trying to answer Schramm’s question, and his approach looked remarkably similar to the Ukrainian team’s, though he’d gotten stuck. The quartet invited him to join them. It was then that Nazarov realized something that the rest of them had missed: The shape their seed gave them did not just contain a constant-width body. It was one.

Andrii Arman (left) and Andriy Prymak comprise half of a four-person team of mathematicians from Ukraine who have been collaborating for years.
Jaskaran Singh
Their work provides a surprisingly simple algorithm for building an n-dimensional shape of constant width whose volume is at most 0.9n times that of the ball. That limit is, in a sense, arbitrary, Arman said. It should be possible to find even smaller bodies of constant width. But it is enough to answer Schramm’s question, proving that as the number of dimensions increases, the gap between the volumes of the smallest and largest constant-width bodies grows exponentially. Despite the complex ideas behind their result, Arman said, their construction is something undergraduates should be able to verify.
Moving On
For Gil Kalai of Hebrew University, there is personal satisfaction in seeing an answer for Schramm, his former student, who died in 2008 in a hiking accident after making significant advances on questions in many different fields. But Kalai is also excited to explore the theoretical consequences of the result. Previously, he said, it was possible that in higher dimensions, these shapes would all simply behave like balls, at least when it came to the property of volume. But “this is not the case. So this means that the theory of these bodies in high dimensions is very rich,” he said.
That theory might even have applications. In lower dimensions, after all, bodies of constant width are already surprisingly useful: The Reuleaux triangle, for example, shows up in the form of drill bits and guitar picks and tamper-proof nuts for fire hydrants. According to Arman, in higher dimensions, their new shapes might be useful in the development of machine learning methods for analyzing high-dimensional data sets. Bondarenko — known within the group for what Arman calls his “crazy ideas” — has also proposed connections to distant branches of mathematics.
The search for the smallest possible body of constant width — which remains open in all dimensions greater than 2 — continues. The group briefly used their construction to investigate one promising candidate in three dimensions, but it let them down: It turned out to be a tiny fraction of a percent larger than the smallest known body. For now, the mathematicians have decided to give up the chase and return to their work on Borsuk’s problem. In their wake, they’ve left behind a world of new high-dimensional shapes for others to explore.



