Mathematician Measures the Repulsive Force Within Polynomials

Just as a magnetic field pushes apart iron filings, a repulsive force acts on the roots of polynomials.
Quanta Magazine; source: Windell Oskay
Introduction
In the physical world, objects often push each other apart in an orderly way. Think of the symmetric designs formed by iron filings under the influence of a magnetic field, or the even spacing of parkgoers practicing social distancing.
When mathematicians look at the number line, they see the same type of trend. They look at the tick marks denoting the positive and negative counting numbers and sense a kind of numerical force holding them in that equal spacing. It’s as though, like mountain lions with their wide territories, integers can’t exist any closer together than 1 unit apart.
The spacing of the number line is the most basic example of a phenomenon found throughout the field of number theory. It crops up in the study of prime numbers and in the relationships between solutions to different types of equations. Mathematicians can better understand these important values by quantifying the force that acts between them.
“Things with number-theoretic significance tend to push each other apart. The name for this is a repulsion principle,” said Jacob Tsimerman of the University of Toronto. “We try to obtain repulsion principles and use them to get various other results.”
A lot of important work in number theory has to do with the way a repulsion principle influences polynomials, collections of coefficients and variables raised to powers. And for decades, mathematicians have been trying to pin down the exact magnitude of the repulsion in this setting.
In a proof posted online in late December, Vesselin Dimitrov of the University of Toronto finally did it.
“It is truly spectacular,” said Péter Varjú of the University of Cambridge over email. “Vesselin’s idea is completely new, and it is beautiful.”
The problem Dimitrov solved, known as the Schinzel-Zassenhaus conjecture, is about the geometry of values of polynomials. It predicts that when you graph certain values, they’ll be spread out in an exact way, looking as if they’re pushing each other apart. Dimitrov’s work exactly quantifies this spreading out, proving the conjecture true. It also provides new insight into the laws that numbers seem to obey.
“This result plants a flag in the ground in terms of our understanding of algebraic numbers,” Tsimerman said.
The Roots of Unity
When studying polynomials, mathematicians are especially interested in their “roots,” the values of a variable that make the polynomial equal zero. A polynomial has as many roots as its degree, or the value of its largest exponent. So x2 − 4 has two roots (2 and −2), while x5 − 7x3 + 2x2 − 4x − 9 has five roots.
Mathematicians want to know how the roots of a polynomial relate to each other. For example, when graphed, the roots of some polynomials fall exactly on the vertices of regular polygons — they stand apart by an exact geometric length. Mathematicians are interested in finding other, more subtle geometric relationships between roots.
“What kinds of patterns can you get? Can you get any patterns, or are the patterns somewhat restricted?” said Emmanuel Breuillard of Cambridge.
The problem that Dimitrov solved involves the roots of a particularly important family of expressions called the cyclotomic polynomials. These polynomials can’t be factored into smaller ones, but you can use them to build other polynomials — they’re like the elements in a periodic table of polynomials. The first and simplest cyclotomic polynomial is x − 1, and the second is x + 1. The tenth is x4 − x3 + x2 − x + 1. Unlike the periodic table, however, the list of cyclotomic polynomials goes on forever.
The roots of cyclotomic polynomials follow a very special geometric pattern. To see it, start with the empty complex plane, in which the x-axis plots real numbers and the y-axis plots imaginary ones. Then inscribe a circle with a radius of 1 around the origin. This is the unit circle. The roots of cyclotomic polynomials all lie on this circle. They bear an elegant name: “roots of unity.”
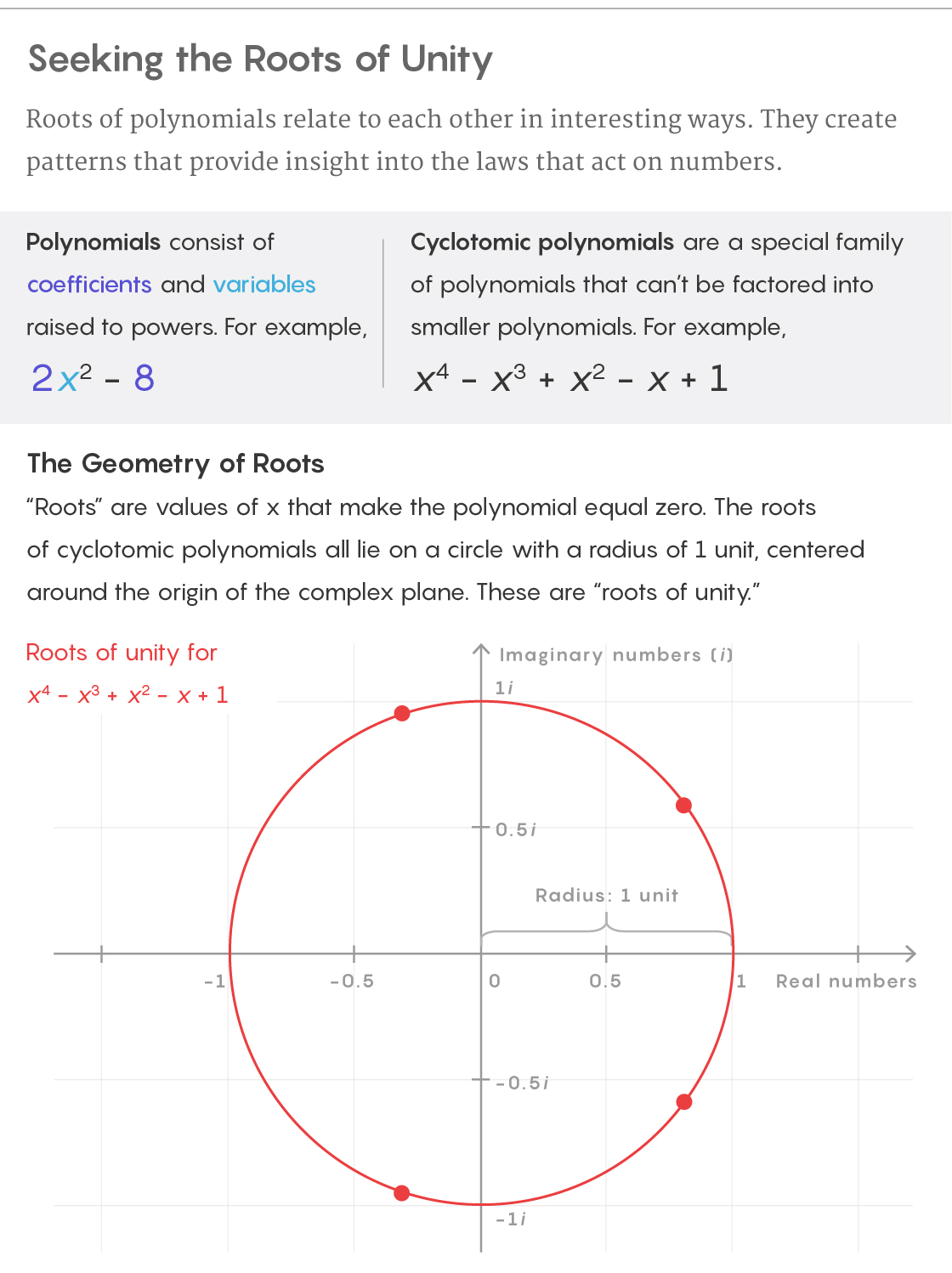
5W Infographics for Quanta Magazine; source: Alex Kontorovich
But most polynomials are non-cyclotomic, and their roots are not roots of unity. This is the case with almost any combination of coefficients, variables and exponents you could come up with.
In 1965, Andrzej Schinzel and Hans Zassenhaus predicted that the geometry of the roots of cyclotomic and non-cyclotomic polynomials differs in a very specific way. Take any non-cyclotomic polynomial whose first coefficient is 1 and graph its roots. Some may fall inside the unit circle, others right on it, and still others outside it. Schinzel and Zassenhaus predicted that every non-cyclotomic polynomial must have at least one root that’s outside the unit circle and at least some minimum distance away.
Or, to put the Schinzel-Zassenhaus conjecture in terms of repulsion, it predicted that the smallest roots of a non-cyclotomic polynomial — which might fall within the unit circle — effectively push other roots outside the unit circle, like magnets pushing each other away.
“You can think of the roots of a polynomial as negatively charged particles that repel each other with a force that decays when the distance increases,” Breuillard said.
The Schinzel-Zassenhaus conjecture even defined exactly how strong that repulsive force should be. “It says there’s a very precise, quantifiable sense in which the roots can’t all be very close to the unit circle,” Tsimerman said.
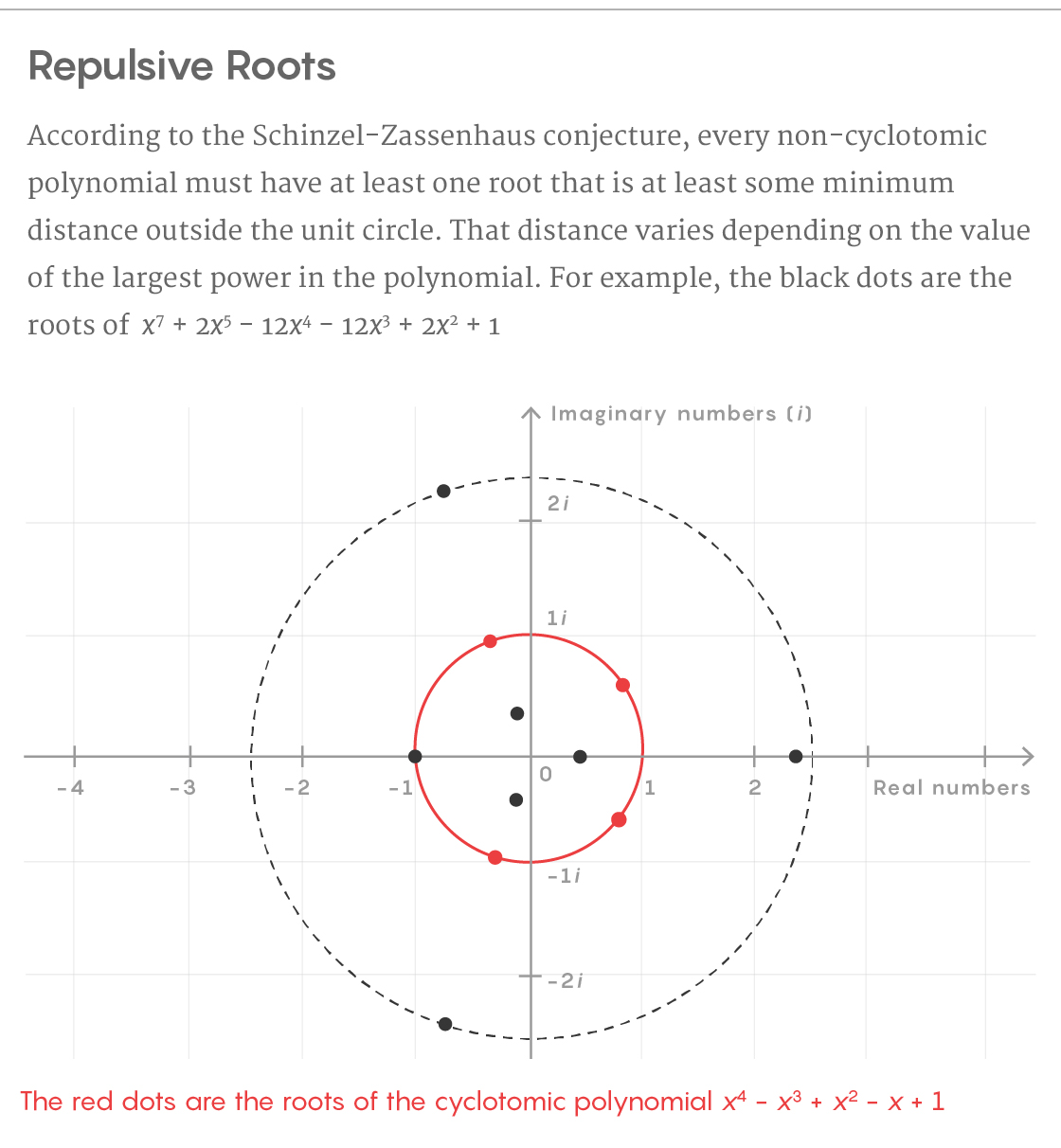
5W Infographics for Quanta Magazine; source: Alex Kontorovich
The conjecture’s main prediction has the feel of a physics equation. It says every non-cyclotomic polynomial should have at least one root that is outside the unit circle by a distance equal to a constant number divided by the degree of the polynomial. The exact value of that constant is not critical, so for the sake of an example, say it’s 0.1. If we had a non-cyclotomic polynomial of degree 23, the conjecture predicts that it should have a root at least .1/23 outside the unit circle.
It’s a powerful statement, but for decades mathematicians only managed to confirm weaker versions of the conjecture’s prediction.
Schinzel and Zassenhaus themselves proved that every non-cyclotomic polynomial has a root at least 1 over 4 raised to the degree of the polynomial (1/4d) outside the unit circle. This distance is much smaller than the conjectured one due to the presence of an exponent in the denominator.
Over the next three decades mathematicians made a series of improvements on Schinzel and Zassenhaus’ work, but the progress remained incomplete. Mathematicians thought the correct distance should be one size, but they could only prove it was at least some smaller size. Mathematicians had no idea how hard the Schinzel-Zassenhaus conjecture would be to solve, assuming it could even be solved at all.
“One never ultimately knows at the outset how simple or complicated [a problem’s] solution will turn out to be — until that solution is found,” said Dimitrov over email.
A Clever Recombination
Often when a prominent math problem remains open for a long time, it’s because mathematicians simply lack the techniques required to solve it. Dream as you might of flying to the moon, you’re not getting there until someone invents a rocket.
But as it turned out, this problem was different. “The technology has been around for at least 40 years,” Tsimerman said.
Dimitrov transformed a question about the size of roots of polynomials into a question about the size of values associated to a related but different type of mathematical object called a power series. A power series is like a polynomial, only with infinitely many terms.
“As often happens in mathematics, the key insight/breakthrough was to connect two seemingly different problems,” said Frank Calegari of the University of Chicago over email.
Mathematicians are accustomed to moving easily between polynomials and power series and using properties of one to establish properties of the other — but mathematicians before Dimitrov didn’t think to use this correspondence to address the Schinzel-Zassenhaus conjecture.
To prove what he wanted to prove about polynomials, Dimitrov needed the related power series to have a specific, essential property: All the coefficients needed to be positive or negative whole numbers (so no fractions). And when Dimitrov started this work, there was no obvious way to guarantee that would happen.
But in November 2019, while “browsing through a few books and papers in algebraic combinatorics,” Dimitrov realized there was a way to cobble together a few well-known theorems to produce the right relationship between a non-cyclotomic polynomial and its power series. He took a non-cyclotomic polynomial, found its roots, raised those roots to different powers, multiplied them together, then took the square root of that product. Then, finally, based on that square root, he could construct a power series with the essential property.
“This was a surprising trick to me, that we take the square root of that product,” said Dimitrov. It was all so unexpected and helpful that Dimitrov calls the fact that it works a “small miracle.” This enabled the next steps in his proof.
Dimitrov proved that the coefficients of the power series are whole number integers. These are always “large” in a sense — they must be at least 1. Because of this, other values related to the power series — its “Hankel determinants” — also have to be large. Through a careful chain of argument, he proved that if coefficients are whole number integers and the Hankel determinants are large, then one of the roots of the non-cyclotomic polynomial he began with must also be large. Much of the work of the proof was in rigorously proving that connection.
“The implication that the coefficients being not small implies what Dimitrov is seeking is quite subtle. It is not something that’s deduced in a direct way,” said Umberto Zannier of Scuola Normale Superiore in Pisa.
Dimitrov proved that all non-cyclotomic polynomials must have a root that’s at least log 2 divided by four times the degree of the polynomial outside the unit circle; that is, (log 2)/(4d). Dimitrov’s result fulfills Schinzel and Zassenhaus’ prediction that the distance is a function of some constant value divided by the degree of the polynomial. And he did it by finding a novel way to combine tools that mathematicians already had on hand.
“He invented the pattern of the proof, which was completely hidden,” said Zannier. “The pieces were already proved, but these pieces were lying in theories which a priori had nothing to do with Schinzel-Zassenhaus.”
Dimitrov’s proof solves one of the main problems in number theory about the patterns that appear within polynomials. Future work may tweak the ratio Dimitrov came up with. It’s possible that the exact values are, say, log 3 in the numerator and five times the degree of the polynomial in the denominator. But to mathematicians, the exact value of the constants is just a technicality. It’s the proportions that matter most, and in that sense, Dimitrov has precisely confirmed Schinzel and Zassenhaus’ prediction.
“This result is very crisp and it’s the best possible result,” Breuillard said. “It’s not going to get any better than this.”
Correction: May 14, 2020
A previous version of this article misstated one of the implications of the Schinzel-Zassenhaus conjecture. The article has been revised accordingly.