New Sphere-Packing Record Stems From an Unexpected Source
Introduction
In math, the search for optimal patterns never ends. The sphere-packing problem — which asks how to cram balls into a (high-dimensional) box as efficiently as possible — is no exception. It has enticed mathematicians for centuries and has important applications in cryptography, long-distance communication and more.
It’s deceptively difficult. In the early 17th century, the physicist Johannes Kepler showed that by stacking three-dimensional spheres the way you would oranges in a grocery store, you can fill about 74% of space. He conjectured that this was the best possible arrangement. But it would take mathematicians nearly 400 years to prove it.
In higher dimensions, mathematicians still don’t know the answer. (With the strange exceptions of dimensions 8 and 24.) Over the years, they’ve come up with better packings. But these improvements have been small and relatively rare.
Now, in a short manuscript posted online in April, the mathematician Boaz Klartag has bested these previous records by a significant margin. Some researchers even believe his result might be close to optimal.
A newcomer to this area of study, Klartag achieved his packing method — which works in all arbitrarily high dimensions — by resuscitating an old technique that experts had abandoned decades earlier. The work taps into several long-running debates about the nature of optimal packings in high dimensions. Should they be ordered or disordered? And how snug can they possibly get?
“This is really an amazing breakthrough,” said Gil Kalai, a mathematician at the Hebrew University of Jerusalem. “It’s something that’s excited mathematicians for nearly 100 years.”
Twin Pictures
In 1905, the mathematician Hermann Minkowski established an intuitive way to think about packed spheres. Start with a repeating arrangement of points in space, called a lattice. Then draw a sphere around each point. In this way, the problem of finding an optimal sphere packing in a given dimension actually becomes a problem about finding a lattice whose points are arranged as efficiently as possible. In two dimensions, for instance, the optimal lattice is “hexagonal,” and yields a packing that looks like this:


Mark Belan/Quanta Magazine
But in 1947, a mathematician named Claude Ambrose Rogers offered a different perspective. Start with any lattice, he said — even a suboptimal one. Rather than draw a sphere around each point, draw an oblong shape called an ellipsoid around one point, so that its surface touches but doesn’t extend past other points in the lattice.
Rogers came up with an algorithm that used this ellipsoid as a starting point to then construct a dense sphere packing. Here’s how it worked:

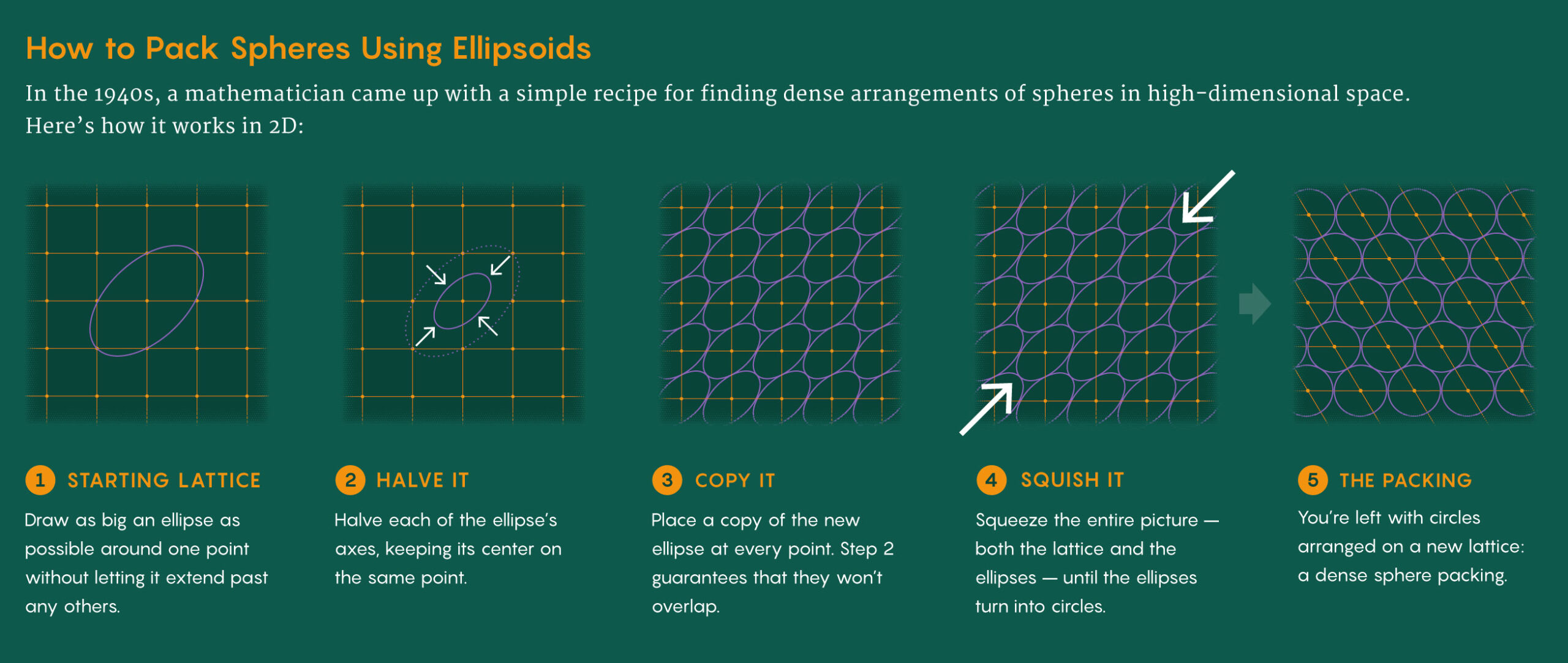
The advantage of Rogers’ method was that you didn’t have to start with a particularly efficient lattice to get an efficient sphere packing. You just had to choose the right ellipsoid. But this introduced a new complication. Unlike a sphere, which is completely defined by a single number — its radius — an ellipsoid is defined by several axes of different lengths. The higher the dimension, the greater the number of directions you can stretch your ellipsoid in, and the more options you have for what your starting ellipsoid will look like.
“In higher dimensions, you have no idea how to grow it. You have too much freedom,” Klartag said.
Mathematicians ultimately returned to Minkowski’s approach, choosing to focus on finding the right lattices. They became more specialized in lattice theory and moved away from Rogers’ focus on geometry.
This strategy led to improvements in high-dimensional sphere packing. But for the most part, they only improved on Rogers’ packing by a relatively small margin. Mathematicians still hoped for a bigger leap.
For decades, they didn’t get it. It would take an outsider to end the stagnation.
An Outside Perspective
Klartag, a mathematician at the Weizmann Institute of Science, was always intrigued by lattices and sphere packing. He just never had the time to learn much about them. He works in geometry, not lattice theory, and he usually studies convex shapes — shapes that don’t jut inward. These shapes involve all sorts of symmetries, particularly in high dimensions. Klartag is convinced that this makes them extremely powerful: Convex shapes, he argues, are underappreciated mathematical tools.

Boaz Klartag long suspected that methods from the field of convex geometry could be useful for sphere-packing problems. He just never had the time to test out his hunch — until now.
Ohad Herches
Then last November, after completing a major project in his usual area of study, he noticed his calendar was uncharacteristically clear. “I thought, I’m 47 years old, all my life I wanted to study lattices, if I don’t do it now then it’s never going to happen,” he said. He asked a friend, Barak Weiss of Tel Aviv University, to mentor him in this new endeavor.
Weiss started a small seminar with Klartag and a handful of others to study the literature. Klartag’s homework included a close reading of Minkowski’s and Rogers’ sphere-packing recipes.
When he read Rogers’ trick for turning an ellipsoid into a sphere packing, he wondered why mathematicians had given up on the method. Ellipsoids are convex shapes, so Klartag knew lots of sophisticated ways to manipulate them. He also realized that the starting ellipsoids that Rogers had used were intuitive but inefficient. All he needed to do was construct a better ellipsoid — one that encompassed more space before its boundary hit other points in the lattice — and he could set a new packing record.
He started with a method he knew well for growing and shrinking the boundary of an ellipsoid along each of its axes according to a random process. Whenever the boundary expanded enough to touch a new point in the lattice, he froze the ellipsoid’s growth in that direction. This ensured that the point would never fall inside the ellipsoid. But the shape continued to inflate in every other direction, until it ran into another point. In this way, the ellipsoid would change shape in jerky, hesitating motions, gradually exploring the space around it. Eventually, the boundary would hit enough points to prevent the ellipsoid from growing further.
Over time, on average, the technique led the ellipsoid to increase in volume. But did it increase enough to surpass Rogers’ intuitive ellipsoid?
Because Klartag’s process was random, it produced a different ellipsoid every time he implemented it. He evaluated the range of possible volumes these ellipsoids might have. If he could find an ellipsoid that was larger in volume than the one Rogers had used decades earlier, he could then use Rogers’ original method to turn it into a tighter sphere packing.
But Klartag couldn’t find a single ellipsoid that was big enough. So he tweaked the details of his random growth process. After just a week or two, he was able to prove that, at least some of the time, this process would yield ellipsoids that were large enough to set a new record.
He immediately informed Weiss of his result. “Let’s meet next week and I’ll tell you what my mistake was,” Klartag told his mentor. But by then, Klartag had only grown more confident in his proof.
Closing In on the Truth
The proof checked out. Klartag’s new starting ellipsoid, when turned into a sphere packing, gave the most substantial improvement in packing efficiency since Rogers’ 1947 paper. For a given dimension d, Klartag can pack d times the number of spheres that most previous results could manage. That is, in 100-dimensional space, his method packs roughly 100 times as many spheres; in a million-dimensional space, it packs roughly 1 million times as many.
Klartag had broken open a central problem in the world of lattices and sphere packing after just a few months of study and a few weeks of proof writing. “It feels almost unfair,” he said. But that’s often how mathematics works: Sometimes all a sticky problem needs is a few fresh ideas, and venturing outside one’s immediate field can be rewarding. Klartag’s familiarity with convex geometry, usually a separate area of study, turned out to be just what the problem required. “This idea was at the top of my mind because of my work,” he said. “It was obvious to me that this was something I could try.”
His result has also revived a debate in the field about the nature of the optimal packing in arbitrarily high dimensions. For a while, mathematicians considered highly symmetric, lattice-based packings to be the best way to arrange spheres as densely as possible. But in 2023, a team found a packing that didn’t rely neatly on a repeating lattice; before Klartag’s result, it was the record to beat. Some mathematicians saw it as evidence that more disorder was needed in the search for an optimal sphere packing.
Now Klartag’s work supports the notion that order and symmetry might be the way to go after all.
Moreover, there’s been debate about just how dense sphere packings can get. Some mathematicians think Klartag’s packing is just a hair away from optimal — practically as close as possible. Others think there’s still room for improvement. “I really have no idea what to believe at this point,” said Marcus Michelen, a mathematician at the University of Illinois, Chicago. “I think all realities are still on the table.”
The answer matters for potential applications to cryptography and communications. And so Klartag’s result, while not immediately useful for those applications, has generated some tentative enthusiasm. “The problem is huge for engineers, and there’s been little progress,” said Or Ordentlich, an information theorist at the Hebrew University. “So this gets us excited.”
Klartag, for his part, hopes that his work will set off a return to the practices of Rogers’ time, when the fields of convex geometry and lattice theory were far more connected. “I think what we now understand about convex bodies should be useful for lattices, even beyond packing,” he said.
“My goal is to make these two fields less disconnected than they are now,” he added. “This was my plan, and I still want to pursue it.”