
Olena Shmahalo/Quanta Magazine
Youth ruled the year in mathematics. The Fields Medals — awarded every four years to the top mathematicians no older than 40 — went out to four individuals who have left their marks all over the mathematical landscape. This year one of the awards went to Peter Scholze, who at 30 became one of the youngest ever to win. But at times in 2018, even 30 could feel old.
Two students, one in graduate school and the other just 18, in two separate discoveries, remapped the borders that separate quantum computers from ordinary classical computation. Another graduate student proved a decades-old conjecture about elliptic curves, a type of object that has fascinated mathematicians for centuries. And amateur mathematicians of all ages rose up to make significant contributions to long-dormant problems.
But perhaps the most significant sign of youth’s rise was when Scholze, not a month after the Fields Medal ceremony, made public (along with a collaborator) his map pointing to a hole in a purported proof of the famous abc conjecture. The proof, put forward six years ago by a mathematical luminary, has baffled most mathematicians ever since.

Major Quantum Computing Advance Made Obsolete by Teenager
This was supposed to be the year that quantum computers finally achieved “quantum supremacy” — indisputable evidence that a quantum machine outclassed an ordinary, classical computer. It was not to be. Quantum machines find themselves having to hurdle an ever-higher bar, since research into quantum algorithms tends to inspire improvements in classical algorithms. This was ever apparent in July when 18-year-old Ewin Tang eliminated what had been one of the clearest, best examples of a problem that quantum computers were thought to be superior at solving. Tang had originally intended to prove that such an algorithm was impossible. The delay in quantum supremacy has even led some theoretical computer scientists to argue that quantum computers will never best classical machines.

Klaus Kremmerz for Quanta Magazine
Titans of Mathematics Clash Over Epic Proof of ABC Conjecture
A mathematical proof is either true or it needs more work, and in theory, any expert mathematician should be able to tell the difference. In practice, however, proofs may be logical, but mathematicians remain human. Rarely has this been more apparent than in the ongoing controversy surrounding the abc conjecture, a major question in number theory. The acclaimed mathematician Shinichi Mochizuki announced in 2012 that he had proven the conjecture. But in the six years since, few researchers outside of Mochizuki’s orbit had been able to follow the enormous, baffling proof, leading some to suspect that its claims would not hold up. In September, Scholze and Jakob Stix of Goethe University Frankfurt announced that they had found what they called a “serious, unfixable gap” in the original work. Mochizuki continues to assert that his proof is both correct and complete.
Just a month earlier, Scholze was awarded a Fields Medal, the highest honor for a mathematician under the age of 40. We profiled him and the other three winners — Caucher Birkar, Alessio Figalli and Akshay Venkatesh — as well as Constantinos Daskalakis, who was awarded the Nevanlinna Prize in theoretical computer science.

Eric Nyquist for Quanta Magazine
Machine Learning Confronts the Elephant in the Room
Artificial intelligence powered by machine learning only grew in importance in 2018. But researchers also continued to probe the limits of where our smartest machines break down. One group found that superimposing a literal elephant onto a picture of a living room made a solid image-recognition system fail in interesting ways. And despite the huge advances that went into game-playing systems that can teach themselves classic board games such as Go and chess, doubts remain as to whether similar systems will ever be able to deal with complicated, real-world scenarios. There’s “really a huge gulf between the real activities of thinking, creative exploration of ideas, and what we currently see in AI,” said Josh Tenenbaum, a cognitive scientist at the Massachusetts Institute of Technology. “That kind of intelligence is there, but it’s mostly going on in the minds of the great AI researchers.”

Jana Ašenbrennerová for Quanta Magazine
Graduate Student Solves Quantum Verification Problem
In October, Urmila Mahadev presented her solution to a basic question in quantum information theory called the quantum verification problem. Mahadev had spent eight years as a graduate student developing a way to ensure that a quantum computer is using some kind of “quantumness” to solve a problem. She was able to engineer such a guarantee by linking quantum computing to classical cryptography in a “truly novel” way, said Thomas Vidick, a computer scientist at the California Institute of Technology. “I expect many more results to continue building on these ideas.”
David Song/Quanta Magazine; Source: Dorian Goldfeld
New Proof Shows Infinite Curves Come in Two Types
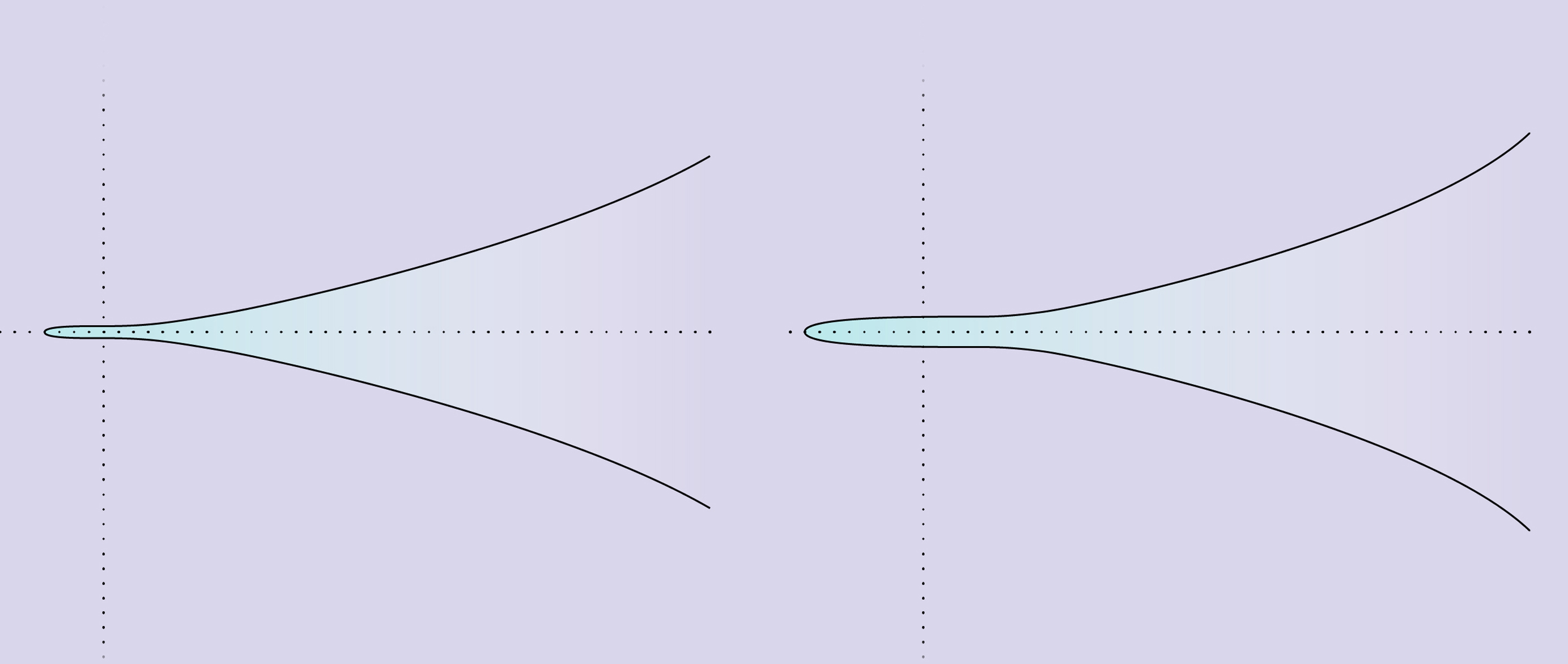
Elliptic curves are fundamental mathematical objects that have played a key role in recent discoveries, including the proof of Fermat’s Last Theorem. In November, we reported on a little-noticed paper from 2017 in which Alexander Smith, a graduate student at Harvard University, proved a 40-year-old conjecture about elliptic curves. He found that exactly half of elliptic curves come with a “rank” of 0, and half with a rank of 1. (This despite the fact that there are an infinite number of elliptic curves that have a rank greater than 1. Blame the tricky statistics of infinity.)
DVDP for Quanta Magazine
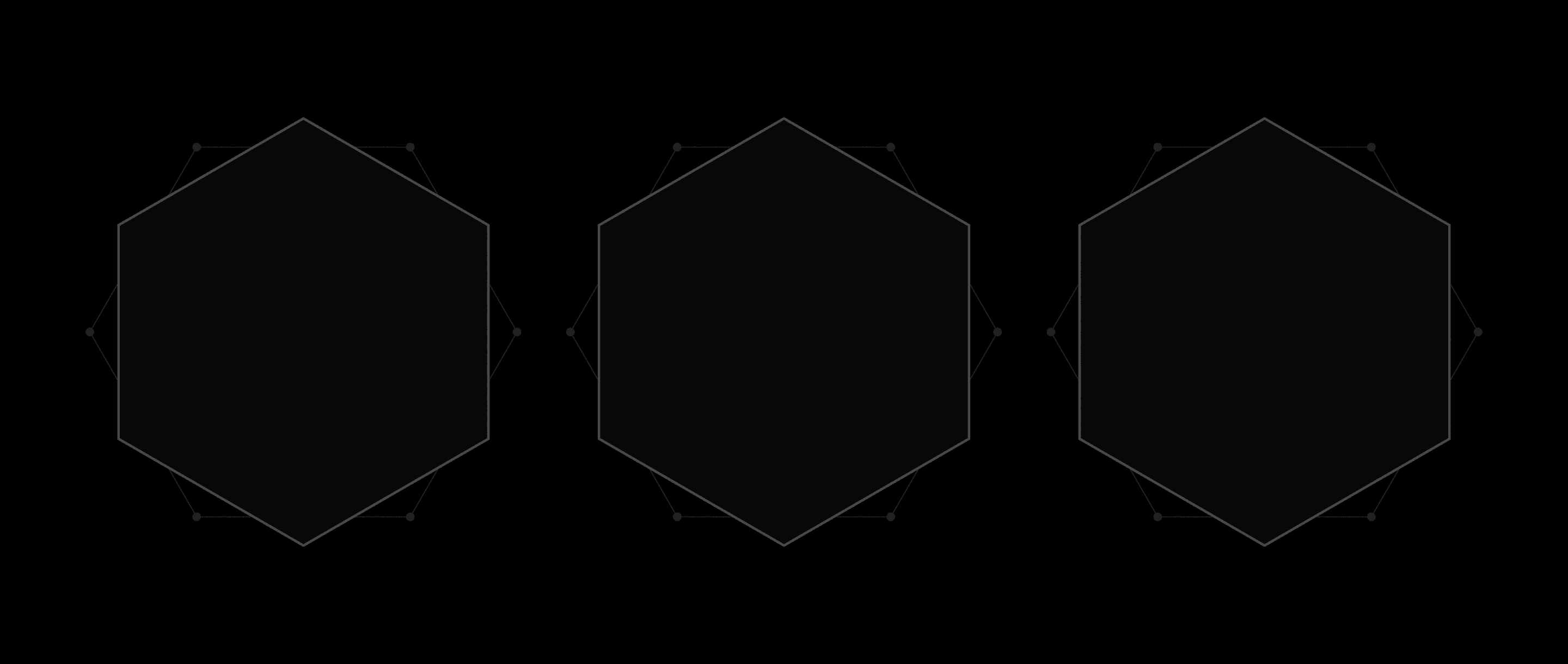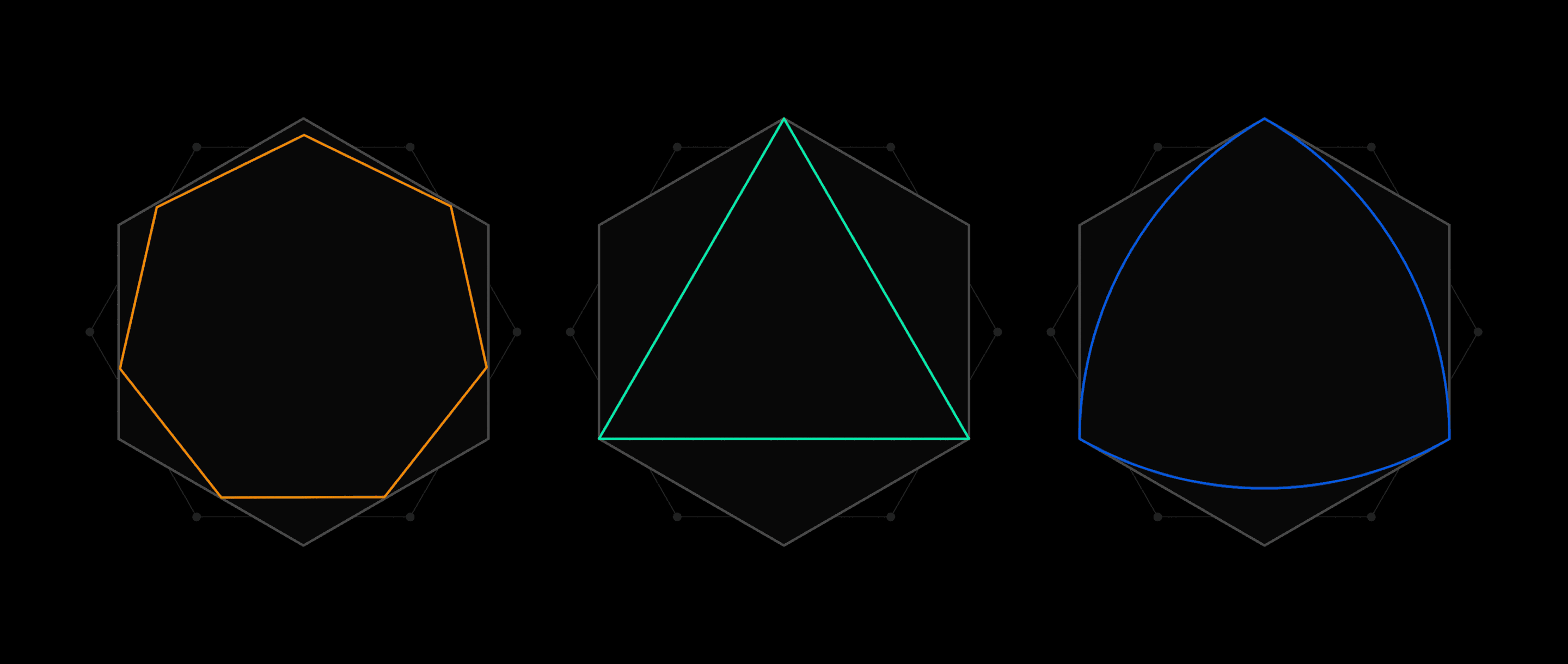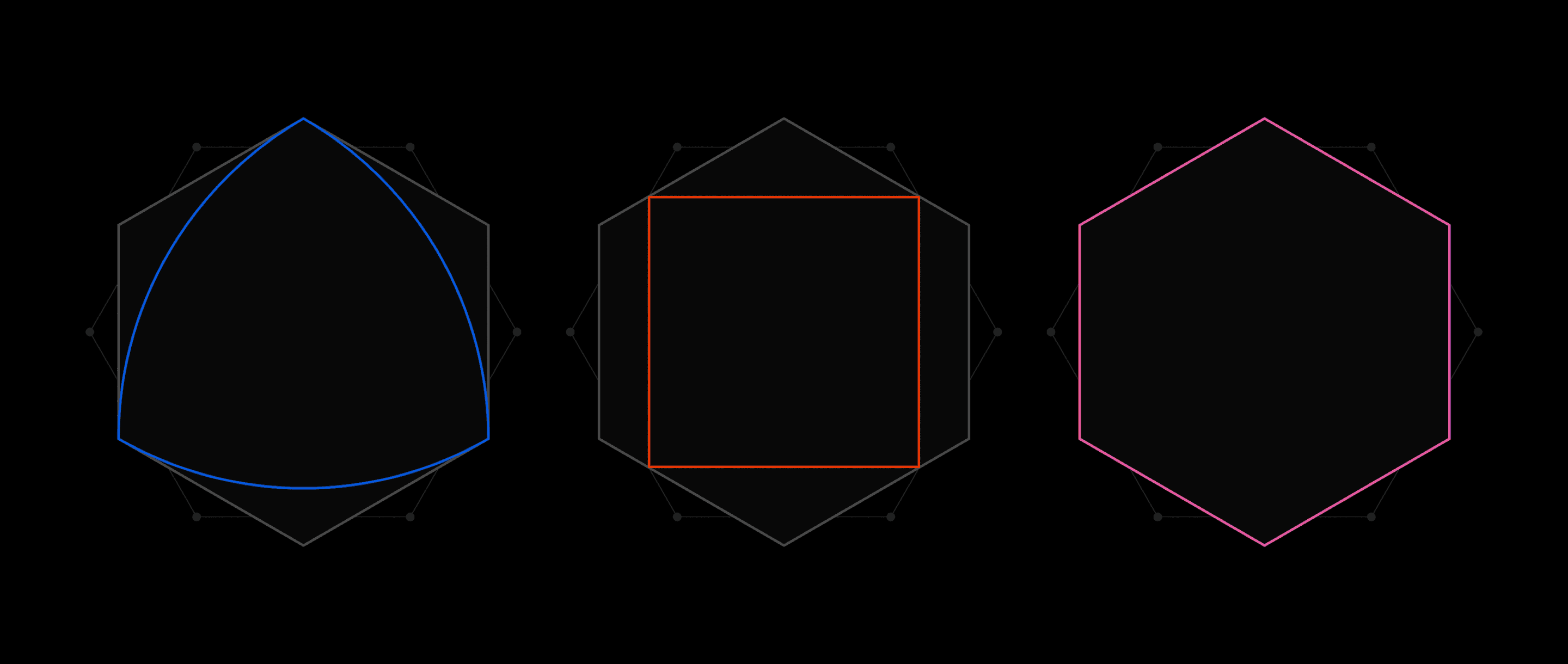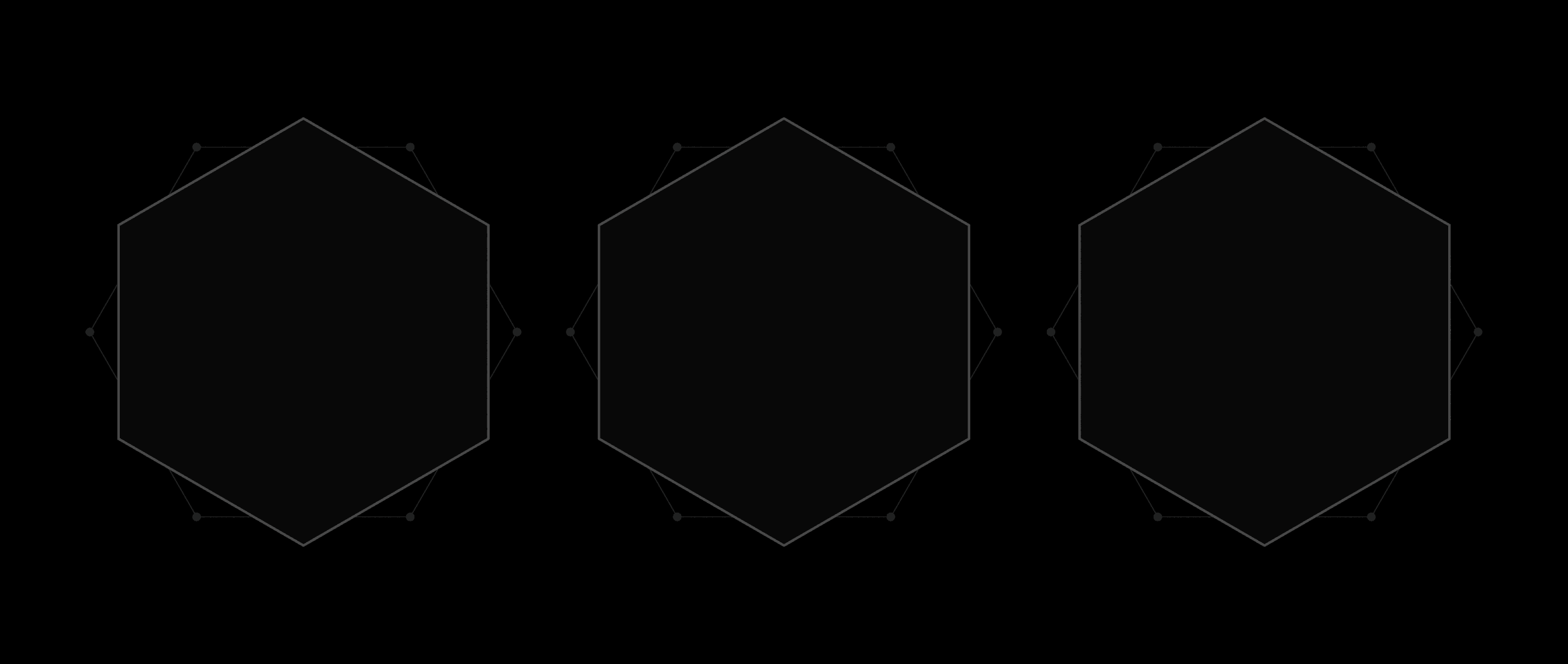
Amateur Mathematician Finds Smallest Universal Cover
Amateur mathematicians had a big year. An anonymous online commenter and a science fiction writer each made a major advance on a 25-year-old question about permutations. The co-founder of an anti-aging organization made the first progress on the “chromatic number of the plane” problem in 60 years. And a retired software engineer found the smallest “universal cover” — an object that can cover up any other two-dimensional shape with radius one.



