The Future of Quantum Computing
Latest Articles
New Strides Made on Deceptively Simple ‘Lonely Runner’ Problem
A straightforward conjecture about runners moving around a track turns out to be equivalent to many complex mathematical questions. Three new proofs mark the first significant progress on the problem in decades.
Can the Most Abstract Math Make the World a Better Place?
Columnist Natalie Wolchover explores whether applied category theory can be “green” math.
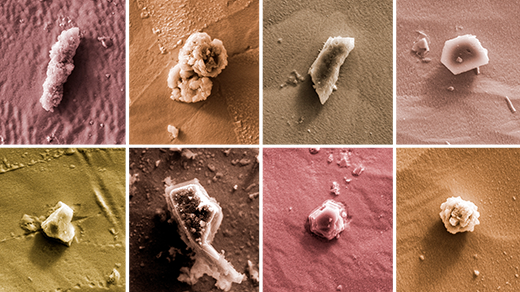
What Crystals Older Than the Sun Reveal About the Start of the Solar System
Microscopic crystals extracted from meteorites could help settle a debate about the birth of our patch of the Milky Way.
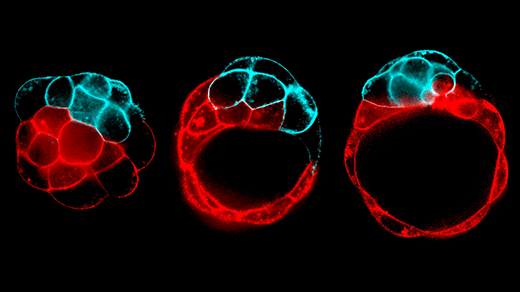
Break It To Make It: How Fracturing Sculpts Tissues and Organs
Growing tissues can crack, break, and dissociate to form structures that can later withstand immense forces.
The Man Who Stole Infinity
In an 1874 paper, Georg Cantor proved that there are different sizes of infinity and changed math forever. A trove of newly unearthed letters shows that it was also an act of plagiarism.
The Evolving Foundations of Math
An exploration of how mathematicians are still renovating and rebuilding the core pillars of their field today.
How Can Infinity Come in Many Sizes?
Intuition breaks down once we’re dealing with the endless. To begin with: Some infinities are bigger than others.
Climate Physicists Face the Ghosts in Their Machines: Clouds
The planet is getting hotter, but one factor in particular makes it hard to tell just how hot it will get. Physicists and computer scientists are racing to solve the problem of clouds.
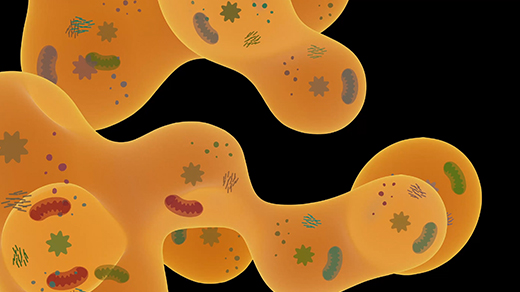
The Biophysical World Inside a Jam-Packed Cell
Innovations in imaging and genetic engineering are coming together to probe the biophysics of cytoplasm inside living animals.