‘Ten Martini’ Proof Uses Number Theory To Explain Quantum Fractals

Wei-An Jin for Quanta Magazine
Introduction
In 1974, five years before he wrote his Pulitzer Prize–winning book Gödel, Escher, Bach: An Eternal Golden Braid, Douglas Hofstadter was a graduate student in physics at the University of Oregon. When his doctoral adviser went on sabbatical to Regensburg, Germany, Hofstadter tagged along, hoping to practice his German. The pair joined a group of brilliant theoretical physicists who were agonizing over a particular problem in quantum theory. They wanted to determine the energy levels of an electron in a crystal grid placed near a magnet.
Hofstadter was the odd one out, unable to follow the others’ line of thought. In retrospect, he’s glad. “Part of my luck was that I couldn’t keep up with them,” he said. “They were proving theorems, but they had nothing to do with the essence of the situation.”
Hofstadter instead decided to test out a more down-to-earth approach. Rather than proving theorems, he was going to crunch some numbers using an HP 9820A desk calculator — a computerlike machine that weighed nearly 40 pounds and could be programmed to perform complex computations.
Hofstadter needed it to solve a particular formulation of the Schrödinger equation, which lies at the core of quantum mechanics. When fed certain information about an electron and its environment as inputs, the Schrödinger equation describes how the electron will behave. In particular, its solutions tell you the amount of energy the electron can have.
In the case that Hofstadter was interested in, the Schrödinger equation includes a variable called alpha, the product of the magnetic field’s strength and the area of one grid square. Alpha captures information about the forces acting on the electron.

Douglas Hofstadter is the author of the Pulitzer Prize–winning book Gödel, Escher, Bach: An Eternal Golden Braid, which examines the self-referential nature of mathematics, music and more.
Courtesy of Douglas Hofstadter
The team of mathematicians in Germany knew that when alpha was rational — that is, either a whole number or a fraction — solving the Schrödinger equation was arduous but possible (so long as you had a big enough calculator). But when alpha was irrational, meaning that it could not be written as a fraction, they had no idea how to solve it.
Instead of struggling with the irrational case like his colleagues, Hofstadter started with what he knew. He programmed his calculator to take a rational value of alpha as an input and print the output on a roll of paper. The result represented the electron’s permitted and forbidden energy levels.
Every evening, Hofstadter would leave his calculator whirring. The next morning, he’d return to a scroll of paper unfurling from the machine, listing the locations of the permitted energies for each rational value of alpha he’d set as an input. He taped together a few pieces of graph paper and, using a felt-tip pen, began meticulously graphing these energy values. That picture would come to be known as the Hofstadter butterfly, because of the resemblance of the graph’s negative space to the insect’s patterned wings.
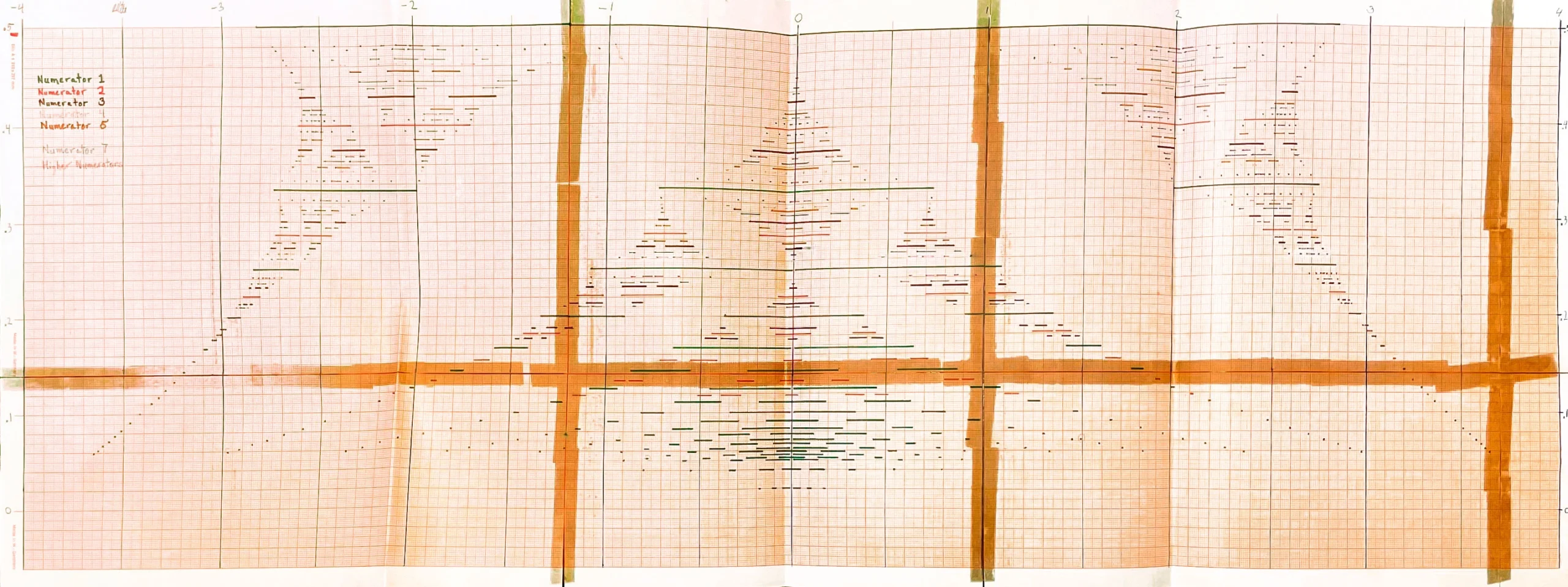
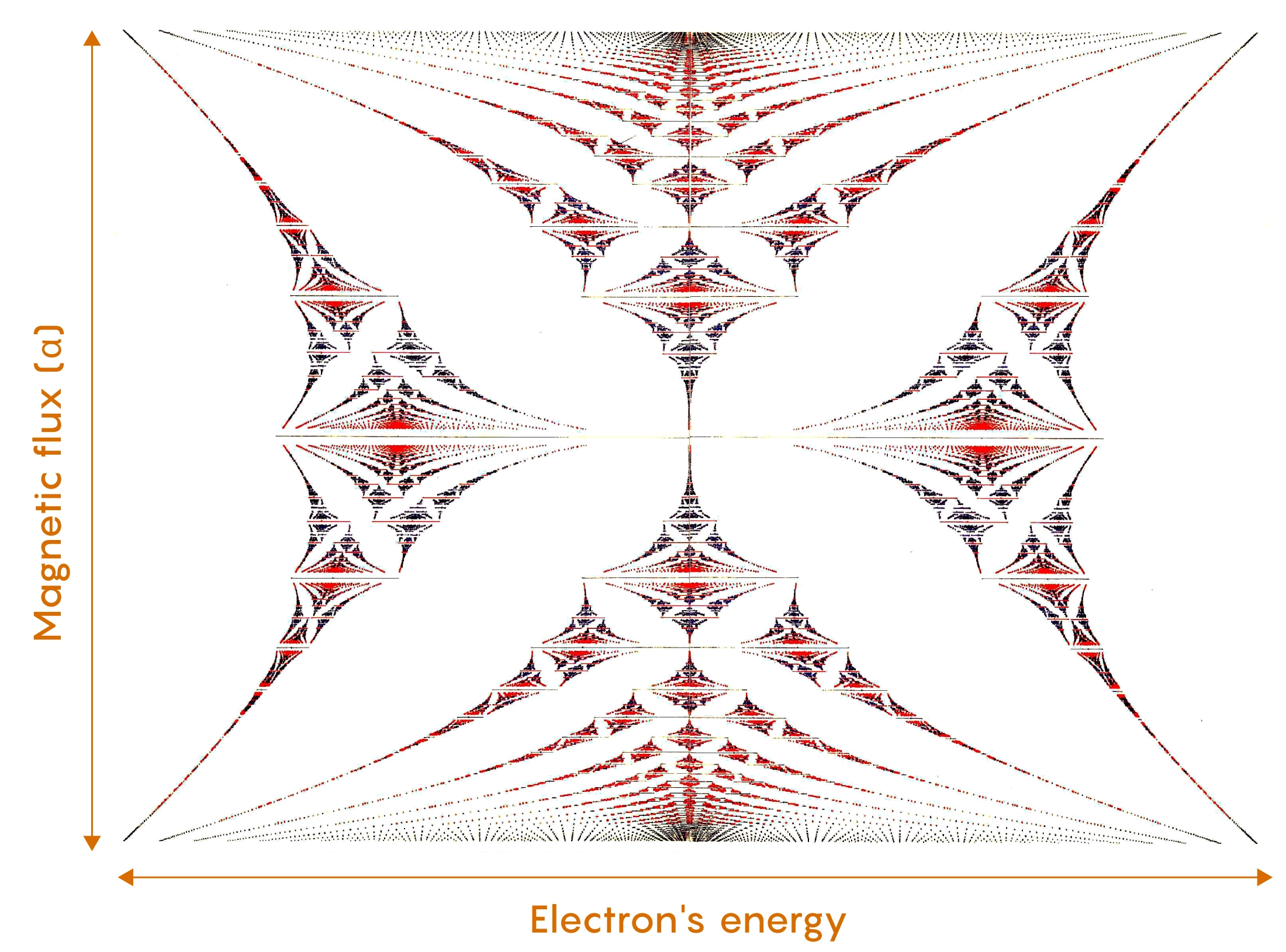

When a crystal is placed near a magnet, its electrons can only have certain amounts of energy. These energy values depend on the crystal’s magnetic flux, which measures how much force the electron is subjected to. In 1974, Hofstadter graphed this phenomenon (top). The vertical axis represents the magnetic flux; the horizontal axis represents the electron’s possible energy values. Hofstadter noticed that the energies formed fractal patterns. The completed graph (bottom) has since been named the Hofstadter butterfly.
Courtesy of Douglas Hofstadter (top); Douglas Hofstadter CC BY SA 3.0 via Wikimedia Commons
Hofstadter’s colleagues couldn’t understand the point of his laborious approach. They joked that he was trying to spin straw into gold and took to calling his calculator “Rumpelstilzchen.”
Even his adviser dismissed the effort as “numerology” and threatened to drop his funding. “He was implying that I was being superstitious and talking nonsense,” Hofstadter said. “Finding meaning and patterns in numbers when they don’t exist.”
But the butterfly that began to emerge on his graph paper intrigued him. Hofstadter noticed that when he entered a fraction, the allowed energies would be broken up by long stretches of forbidden values. As the fraction got more complicated, with more digits in the denominator, the breaks between possible energies got more numerous. The energy values began forming a visually striking pattern — a fractal, meaning that smaller parts of it looked the same as the whole.
His gut told him that it reflected a deep mathematical truth. “It was very clear to me that I had a tiger by the tail,” he said. He recognized the tiger. It was the Cantor set.
The set is named for the mathematician Georg Cantor, who popularized it in 1883 by following a simple rule: Take a line segment, split it into three equal sections, then erase the middle third. This leaves you with two segments separated by a gap. Now erase the middle third of each of these, and so on. If you carry out this procedure infinitely many times, you get an infinite set of points, spread out like dust along the number line.
Merrill Sherman/Quanta Magazine
Hofstadter would never plug in an irrational value of alpha. Irrational numbers can’t be expressed as a fraction — it would require infinitely many digits in the numerator or denominator, something that was impossible to program the calculator to handle. But he noticed that as the rational values of alpha got closer and closer to an irrational number, the set of permitted energy values — the bands of ink in each row of his butterfly picture — looked more and more like a Cantor set. And so, he hypothesized, when alpha was irrational, the possible energies would form an actual Cantor set.
Several years later, two prominent mathematicians came to the same conclusion from a very different direction. Barry Simon and Mark Kac had been studying what they called almost-periodic functions. The outputs of a periodic function, like a sine wave, repeat over and over again. But an almost-periodic function traces out a path that comes very close to repeating, yet never does.
In 1981, Kac and Simon met for lunch and got to discussing the version of the Schrödinger equation that Hofstadter and his colleagues were trying to solve. When alpha was an irrational value, the equation turned into an almost-periodic function. It was exactly the kind of phenomenon they’d been studying. And based on what they knew about almost-periodic functions, Hofstadter was right: The allowed energy levels should form a Cantor set when alpha is irrational.
But Simon and Kac couldn’t prove it either. Kac said he’d buy 10 martinis for anyone who could. Simon began to publicize Kac’s offer, and the problem became known as the ten martini conjecture.

The mathematician Mark Kac once offered 10 martinis to whoever could solve an important problem in quantum theory. He died before the proof was completed in 2004. Above, a group of mathematicians who worked on the problem celebrate the proof in his honor at a conference held that year.
Courtesy of Michael Aizenman
Over the years, mathematicians chipped away at it, proving the conjecture for certain irrational values of alpha (but not all). Simon announced one of these intermediate results in 1982. Kac offered him three martinis. When Kac died in 1984, the problem remained open. A proof worth all 10 martinis wouldn’t appear for another 20 years.
Just a Tad Dirty
In 2003, Svetlana Jitomirskaya, who had spent years studying the almost-periodic function embedded in the Schrödinger equation, had just given up on her career-long goal of proving the ten martini conjecture. A year earlier, a competitor named Joaquim Puig had proved it for all but a few classes of irrational alpha values. What’s more, he’d used techniques she’d published earlier to do it. “I was kicking myself,” she said. “All the hard work was in my proof, and then here he comes with this beautiful argument.”
So she was surprised when a 24-year-old mathematician named Artur Avila visited her and suggested they work on the remaining values of alpha. “I told him it would be very difficult, very time consuming, and no one would care,” she said.
People did. Their proof, which they posted online in 2005, was eventually published in the Annals of Mathematics, the field’s most prestigious journal. Avila later won a Fields Medal in part for his work on the problem.
They decided to honor the 10-martini contract themselves. “We had plenty of celebratory beverages, martinis included,” Jitomirskaya said.

Svetlana Jitomirskaya has spent decades studying subtle patterns that emerge from the quantum behavior of electrons.
Monica Almeida
But in some ways, the proof was a bit unsatisfying. Jitomirskaya and Avila had used a method that only applied to certain irrational values of alpha. By combining it with an intermediate proof that came before it, they could say the problem was solved. But this combined proof wasn’t elegant. It was a patchwork quilt, each square stitched out of distinct arguments.
Moreover, the proofs only settled the conjecture as it was originally stated, which involved making simplifying assumptions about the electron’s environment. More realistic situations are messier: Atoms in a solid are arranged in more complicated patterns, and magnetic fields aren’t quite constant. “You’ve verified it for this one model, but what does that have to do with reality?” said Simon Becker, a mathematician at the Swiss Federal Institute of Technology Zurich.
These more realistic situations require you to tweak the part of the Schrödinger equation where alpha appears. And when you do, the ten martini proof stops working. “This was always disturbing to me,” Jitomirskaya said.
The breakdown of the proof in these broader contexts also implied that the beautiful fractal patterns that had emerged — the Cantor sets, the Hofstadter butterfly — were nothing more than a mathematical curiosity, something that would disappear once the equation was made more realistic.
Avila and Jitomirskaya moved on to other problems. Even Hofstadter had doubts. If an experiment ever saw his butterfly, he’d written in Gödel, Escher, Bach, “I would be the most surprised person in the world.”
But in 2013, a group of physicists at Columbia University captured his butterfly in a lab. They placed two thin layers of graphene in a magnetic field, then measured the energy levels of the graphene’s electrons. The quantum fractal emerged in all its glory. “Suddenly it went from a figment of the mathematician’s imagination to something practical,” Jitomirskaya said. “It became very unsettling.”
She wanted to explain it with mathematics. And a new collaborator had an idea for how to do it.
Another Round, With a Twist
In 2019, Lingrui Ge joined Jitomirskaya’s group. He had been inspired by the work she and Avila had done on the ten martini problem, as well as by a direction of research that Avila had been trying to pursue ever since.
Avila had grown tired of the piecemeal approaches that mathematicians used to understand almost-periodic functions. He instead began to develop what he called a “global theory” — a way to uncover higher-level structure in all sorts of almost-periodic functions, which he could then use to solve entire classes of functions in one go.

Lingrui Ge helped develop a new way to understand the solutions to almost-periodic functions, important equations that appear in quantum physics.
Courtesy of Lingrui Ge
To do this, he associated a geometric object to a given almost-periodic function and studied its properties. He realized that some of those geometric properties could help him solve the original function.
But it only worked for certain types of functions. It couldn’t handle the types of calculations that the ten martini problem required. It wasn’t clear that it ever could.
That’s because to prove the ten martini conjecture, mathematicians had to first transform the Schrödinger equation into a related equation called its dual, then solve that new equation. Avila’s theory couldn’t say anything about the higher-level structure of the dual.
Or so he thought. But Ge was intrigued by the geometric objects that Avila had described. He suspected that other properties of those objects hid even more information — information that might illuminate aspects of the dual equation. “I could see that it was a very beautiful and important theory,” Ge said.
He and Jitomirskaya — along with Jiangong You and Qi Zhou of Nankai University in China — figured out a new way to interpret Avila’s geometric object and apply it to the dual. This made the theory far more powerful. It also allowed Ge, Jitomirskaya and You to write a single proof that solved versions of the ten martini problem in lots of different settings. No patchwork quilt needed.
The result cements the Hofstadter butterfly as a real-life phenomenon. The abstract world of number theory holds power in the world of physics.
The mathematicians have since used their version of Avila’s global theory to solve two other key problems in the area. They predict that this is just the beginning of what they can do with the method they’ve uncovered. “We found this hidden mystery behind the global theory,” Ge said. “It was like a beacon on a dark sea that showed us the right direction.”
Correction: August 25, 2025
An earlier version of this article stated that Avila was 26 years old when he began to collaborate with Jitomirskaya on the ten martini problem. He was 24.



