The Sordid Past of the Cubic Formula

History is full of backstabbing rivalries: Edison and Tesla, Harding and Kerrigan, Tupac and Biggie. No less dramatic was a 16th-century conflict between Italian mathematicians Gerolamo Cardano, a brilliant but troubled polymath, and Niccolò Fontana, better known as Tartaglia (meaning “the stammerer,” after a teenage facial injury from a French soldier’s sword). The central issue: cubic equations.

Most high school students know how to solve quadratic equations, such as $latexx^2-x-3=0$, using the quadratic formula. It states that the solutions, or roots, of $latexax^2+bx+c=0$ are

$latexx=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$.

Are there similar formulas for equations of higher degree (having a larger power of x)? Determining this, in essence, was the task before Cardano, Tartaglia and their contemporaries.

Modern algebra as we know it — abstract symbolic expressions like those above and the familiar ways of manipulating them — dates to the 17th century, long after these scholars’ time. But algebraic thinking, and the ability to solve what we recognize as linear and quadratic equations, developed slowly over the preceding millennia.

In the 16th century, algebraic equations were still expressed rhetorically — in words, not symbols — and all coefficients had to be nonnegative, since mathematicians did not recognize negative numbers as legitimate. Without the notion of an unknown variable x, cubic equations of the form  $latexx^3+cx=d$ were instead described as “a cube and things equals a number,” and that was seen as different than “a cube equals things and a number,” $latexx^3=cx+d$. So while today we would view solving $latexax^3+bx^2+cx+d=0$ as one problem, at that time it was viewed as more than a dozen distinct problems, with the terms on one or the other side of the equal sign, or absent entirely.

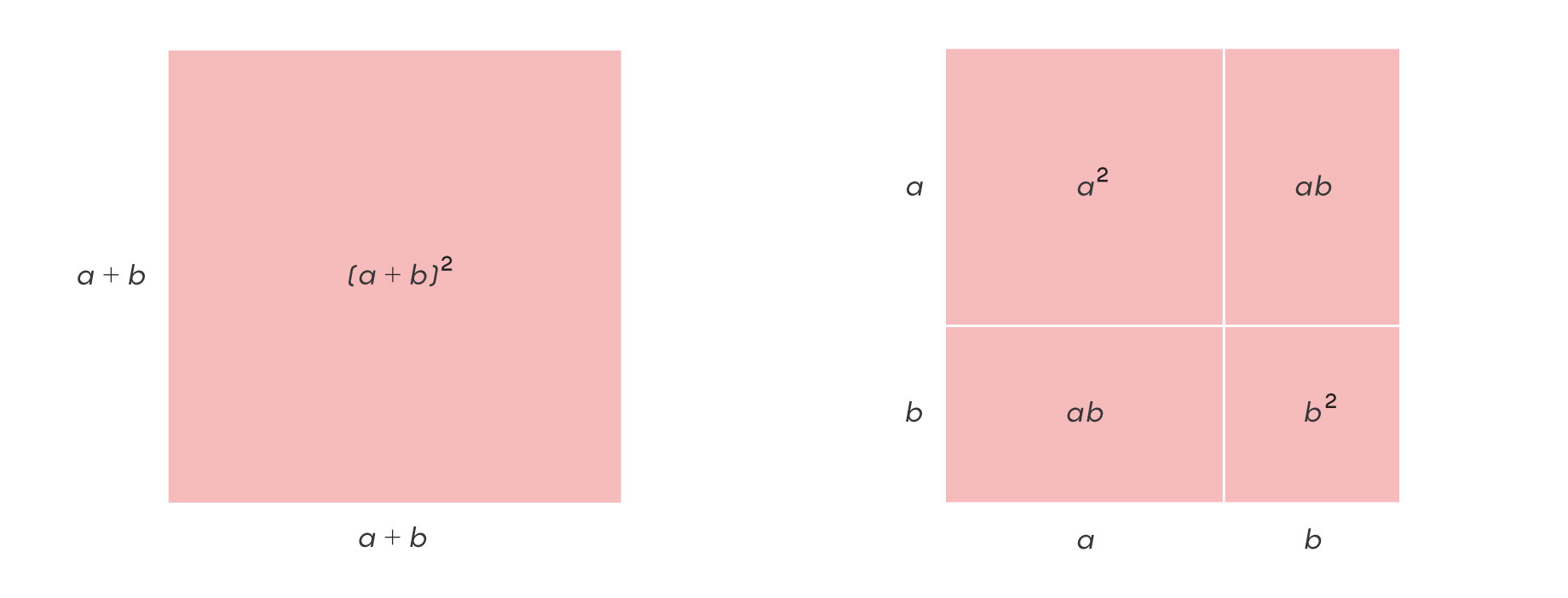
Without modern symbolic algebra, mathematicians would reason geometrically. For instance, we can view the familiar expression $latex(a+b)^2=a^2+2ab+b^2$ as saying that the area of a square of side-length $latexa+b$  is the same as the sum of the areas of a square of side-length a, a square of side-length b, and two $latexa \times b$ rectangles.

Likewise, decomposing a cube with side-length t into six boxes shows that

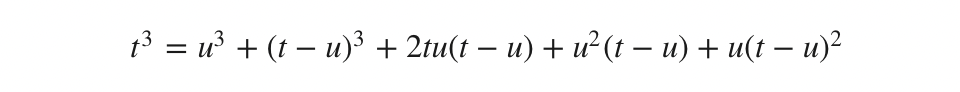
(as long as $latext>u$).

Scipione del Ferro, a professor at the University of Bologna in the early 16th century, was first to make significant headway into solving cubic equations. Unfortunately, we do not know all his accomplishments, thanks to a curious culture of academic secrecy at the time. Rather than racing to publish their work and basking in the recognition of proving a theorem or solving a problem, scholars would challenge each other to “mathematical duels.” They would send each other challenging problems, and the one who solved the most was the winner. The victors often garnered professional advancement and more students. Thus, discoveries would sometimes be held in reserve, secret weapons to be deployed in future contests.

But we do know del Ferro could solve equations of the form $latexx^3+cx=d$, when c and d are positive. A cubic equation with no squared term, such as this one, is called a “depressed cubic.” Although no 16th-century mathematician would express it this way, del Ferro showed that one root is

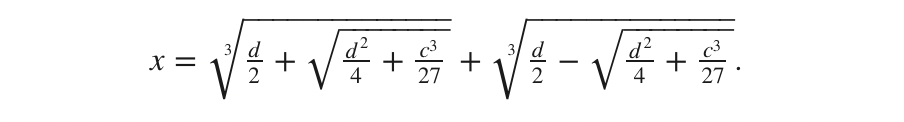
This modern formula applies to any depressed cubic, but because cubic equations with different signs on the coefficients were considered different problems, del Ferro’s solution did not automatically carry over to other depressed cubics. We only know del Ferro could solve these cubics because he taught the technique to his student Antonio Fior, who bragged that he could solve such equations after del Ferro’s death.

Meanwhile, the self-taught Tartaglia discovered how to solve a different form of the cubic — one missing the linear term, cx. This set the stage for a mathematical duel between Fior and Tartaglia. In 1535, they exchanged 30 problems with a deadline of a month and a half. Tartaglia sent Fior a variety of problems, whereas the mathematically weaker Fior employed the “all eggs in one basket” strategy and sent Tartaglia 30 depressed cubics. Just days before the deadline, Tartaglia figured out how to solve them, and in two hours finished all 30. Fior, meanwhile, solved none of his problems. News spread throughout Italy of Tartaglia’s achievement, and Fior, humiliated, faded from view.

The prevailing wisdom was that solving the cubic was impossible, so Tartaglia’s accomplishment shocked Cardano. At this time, Cardano was a highly sought physician but cantankerous, beset by trouble after trouble. He gambled, he struggled with misbehaving sons, he was jailed during the Inquisition and more. Yet he ended up making contributions in mathematics, medicine, philosophy, religion, music and physics. Decades later, Gottfried Leibniz wrote, “Cardano was a great man with all his faults; without them, he would have been incomparable.” His collected works fill 7,000 pages and include the first serious investigations of probability theory.

Cardano tried, and failed, to replicate Tartaglia’s success with the cubic, so he began a pressure campaign to convince Tartaglia to share his method, even promising a vow of secrecy:

I swear to you by the Sacred Gospel, and on my faith as a gentleman, not only never to publish your discoveries, if you tell them to me, but I also promise and pledge my faith as a true Christian to put them down in cipher so that after my death no one shall be able to understand them.

Eventually, in 1539, Tartaglia relented and shared his technique for depressed cubics with Cardano, but he did not share the proof that it worked. For the clever Cardano, however, just knowing the method was enough to discover the underlying mathematics. Before long, Cardano could solve any depressed cubic. He then observed that substituting

$latexx=t-\frac{b}{3a}$

into $latexax^3+bx^2+cx+d=0$ yields a depressed cubic with variable t. By solving this equation for t and plugging that back into the substitution formula, he could find x. Thus, Cardano was able to solve every cubic equation.

Despite his vow to Tartaglia, Cardano taught these results to his talented assistant Ludovico Ferrari. Although he began as Cardano’s servant, Ferrari eventually became Cardano’s mathematical equal. By helping Cardano with his work on the cubic, he became so algebraically adept that he discovered how to reduce any quartic equation (one of degree 4) to a cubic. Thus, Cardano and Ferrari could solve any equation of degree four or less.

Cardano recognized the importance of these accomplishments and desperately wanted to publish the results. But since they all grew from the seeds planted by Tartaglia, doing so would break his oath.

Then, on a trip to Bologna in 1543, Cardano saw in del Ferro’s notebooks that he had solved the depressed cubic before Tartaglia. In Cardano’s mind, this discovery freed him of his obligation to Tartaglia. Two years later, Cardano published Ars Magna (Great Art), which contained his and Ferrari’s work on cubic and quartic equations.

Tartaglia was livid, even though Cardano acknowledged his work in the book. Tartaglia accused Cardano of theft and of breaking a sacred vow. Cardano left the rebukes to his loyal attack dog, Ferrari. The acrimonious back-and-forth, in the form of public pamphlets, continued for many months, leading to a mathematical duel between Tartaglia and Ferrari and eventually a public debate in Ferrari’s hometown, Milan. Tartaglia would much rather have battled the esteemed Cardano, but Cardano refused. Details are scarce, but the debate went terribly for Tartaglia, especially with the raucous hometown crowd. The next day, when it was time to continue the debate, Tartaglia was nowhere to be found — he’d left Milan.

Ferrari was flooded with job offers, and Tartaglia’s reputation was ruined. Despite many notable accomplishments beyond those related to the cubic, Tartaglia died penniless and largely unknown, whereas Cardano achieved everlasting fame. Many argue that the publication of Ars Magna marked the beginning of modern mathematics.

Having conquered cubic and quartic equations, mathematicians wondered how high they could go. As it turned out, not very far.

The story of quintic equations (polynomials of degree 5) is also fascinating, and it has a shocking conclusion: In general, it is impossible to express the roots of $latexax^5+bx^4+cx^3+dx^2+ex+f=0$ in terms of a, b, c, d, e and f using only addition, subtraction, multiplication, division and nth roots. For instance, the polynomial $latexx^5-x+1$ has a root of approximately $latex–1.167304$, but the exact value is impossible to express with those tools.

Niels Abel gave the first full proof of this fact in 1824, nearly three centuries after Ars Magna. Then, in 1830, the 18-year-old political firebrand Évariste Galois extended this work by giving exact criteria for when a polynomial of any degree is solvable. Although Galois died two years later in a duel (one fought with guns, not mathematics), his contributions to mathematics were oversized.

These impossibility results were not the end of the story. Mathematicians still study polynomials, their roots and their properties. As but one example, a famous problem proposed by David Hilbert in 1900 is about the roots of seventh-degree polynomials. It was thought to have been resolved in the 1950s but is now the subject of renewed interest. Presumably, modern mathematicians can make headway on the problem without re-creating the rivalry surrounding the cubic.

Correction: July 1, 2022
An earlier version of this article incorrectly stated that a root of the polynomial $latex x^5-x+1$ is approximately $latex-1.67304$; the correct value is $latex-1.167304$. Quanta regrets the error.