Using AI, Mathematicians Find Hidden Glitches in Fluid Equations
Samuel Velasco/Quanta Magazine
Introduction
Nearly 200 years ago, the physicists Claude-Louis Navier and George Gabriel Stokes put the finishing touches on a set of equations that describe how fluids swirl. And for nearly 200 years, the Navier-Stokes equations have served as an unimpeachable theory of how fluids in the real world behave — from ocean currents threading their way between the continents to air wrapping around an aircraft’s wings.
Nevertheless, many mathematicians suspect that glitches hide deep within the equations. They have a hunch that in certain situations, the theory fails. In these cases, the equations will predict a fluid moving in some unphysical, incomprehensible way — spinning into an impossibly fast vortex, for instance, or instantly reversing its flow. Some quantity in the equations will grow infinitely large, or “blow up,” as mathematicians put it.
Despite immense effort, no one has been able to come up with a situation where the Navier-Stokes equations falter. Doing so — or, alternatively, proving that the equations never blow up — would come with a $1 million reward. And so, as a prelude to solving the Navier-Stokes problem, mathematicians have searched for blowups (also called singularities) in an assortment of simplified fluid equations, such as those that operate in only one dimension.
They’ve found them. But essentially all the singularities they’ve identified have been “stable,” meaning that they can form in many possible ways. In the most realistic fluid theories, including Navier-Stokes, blowups (if they exist) are likely to be far more delicate, occurring in an unimaginably precise way. These “unstable” blowups have been nearly impossible to find, the ultimate needles in the haystack.
In these realistic theories, “a lot of people believe that there are singularities, but that they are unstable, so we never see them,” said Charlie Fefferman, a mathematician at Princeton University who formulated the million-dollar Navier-Stokes challenge.
Now one group of mathematicians has developed a way of training machines to spot these phantom glitches. In a preprint posted in September, they reexamined simpler fluid equations already known to host a stable singularity. There, they found additional potential blowup scenarios — including unstable ones. It was the first time a possible unstable singularity was uncovered in a fluid of more than one dimension.
The team went on to discover an assortment of unstable singularity candidates in several other fluid equations as well. They have not found any million-dollar singularities. And they still need to rigorously prove that the ones they have found do indeed blow up. But their success in uncovering potential unstable singularities in simple models raises hopes that it will also be possible to find unstable blowups in higher-stakes scenarios.
“The idea of an unstable singularity no longer prevents the discovery of the singularity,” said Fefferman, who was not involved in the new research.
Singularity Hunting
A solution to the Navier-Stokes equations captures a slice of eternity. Solving the equations for some initial state of the fluid will tell you the fluid’s velocity at each point in space and at every moment in time. In one simple solution, a fluid might start calm and remain calm forever. In a more complicated setup, gentle currents might merge into whirlpools and eddies. The great mystery is whether every solution — every single possible fluid history that satisfies the Navier-Stokes equations — makes sense everywhere and always.
But tackling the Navier-Stokes equations for fluids in three dimensions is unspeakably difficult, so mathematicians have started with easier versions of the problem. For instance, the Euler equations assume that fluids flow with no internal friction, or viscosity. Energy doesn’t dissipate in these frictionless fluids, so they should blow up more easily than viscous ones.
But even in this simpler scenario, finding a blowup solution is hard. Fluid equations are generally too complicated to solve directly with pencil and paper. So a common approach is to use a computer to simulate the fluid’s motion and get an approximate sense of the conditions that seem to produce a blowup. If you can narrowly identify the blowup-producing conditions, you might be able to use that knowledge to rigorously prove that a blowup truly exists.
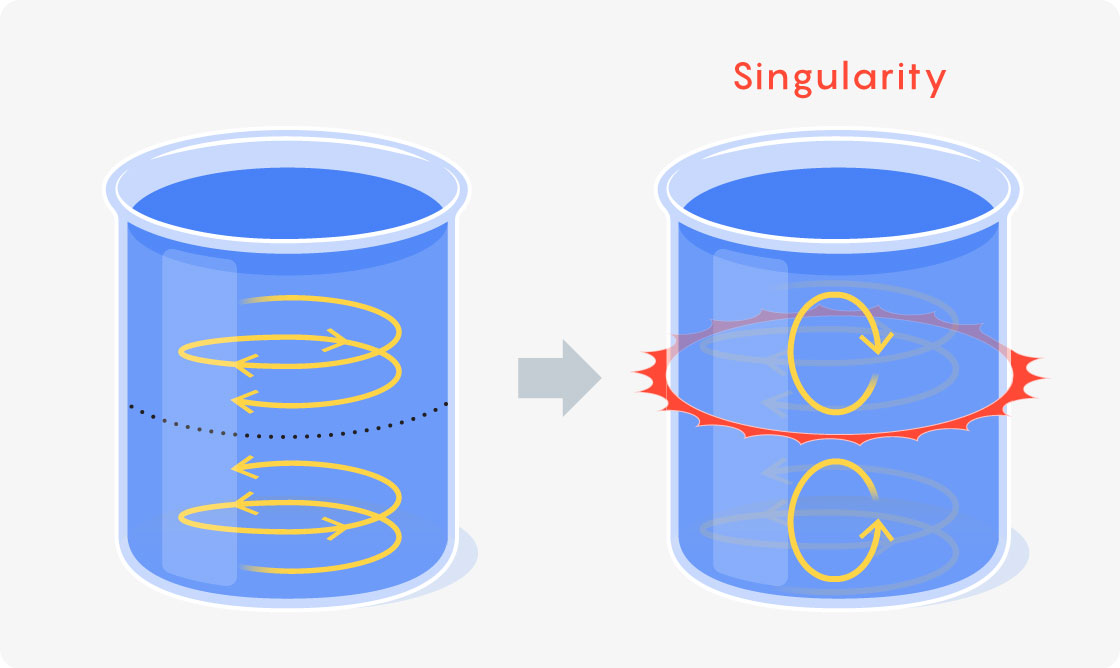
That’s the approach that Thomas Hou and Guo Luo took in 2013, when they simulated a digital liquid in a can. They set the top half of the liquid spinning in one direction and the bottom half in the other, then evolved this scenario through time using the Euler equations. Eventually, at points where the opposing flows met along the can’s boundary, the vorticity (a measure of how much the liquid spins around a point) got big — bigger than their computer could handle.
Mark Belan/Quanta Magazine
This was a hint that a similar set of conditions would lead to a blowup. But it was not a guarantee. “The graveyards are strewn with alleged singular solutions of 3D Euler,” Fefferman said.
It took Hou and another collaborator, Jiajie Chen, nearly a decade to remove the “alleged.” In 2022, they used a computer to prove that the singularity candidate implied the existence of a true singularity. It was a landmark proof, and it got mathematicians hungry to push the frontier even further.
The research depended on computer simulations, which meant that tiny adjustments to the initial state of the digital fluid (or any digital rounding errors) wouldn’t affect the fluid’s fate. A singularity would still occur at the can’s boundary even if things played out a little bit differently.
Because of this, the singularity was stable. But a singularity need not be stable. A blowup might occur only when the fluid is set up in the most delicate of ways. In such a case, any adjustment to that initial arrangement, no matter how small, would prevent the fluid from blowing up.
Many mathematicians conjecture that if singularities do lurk in more realistic fluid equations, they’ll be unstable like this, springing up without warning.
They’ll also be far harder to find.
Going Finite
It’s essentially impossible to track down an unstable singularity candidate with a computer simulation. First you’d need a cosmic stroke of luck to land on exactly the right initial configuration for your fluid — akin to trying to balance a pen perfectly on its tip, said Tristan Buckmaster, a mathematician at New York University. Then, to keep it balanced, you’d also have to evolve the fluid flawlessly from one moment to the next, since even the smallest deviation will tip it onto a path that doesn’t blow up.
Computers aren’t capable of infinite precision. They’ll inevitably introduce numerical errors that, though tiny, will stop the unstable singularity from forming. “It’s like the wind blowing on your pen,” Buckmaster said.
A frictionless fluid spinning against a cylinder can “blow up,” according to a landmark proof from Thomas Hou (left) and Jiajie Chen in 2022.
Vicki Chiu; Courtesy of Jiajie Chen
As a result, almost all blowup candidates have been stable.
So Buckmaster and his colleagues began to work out a potentially wind-proof way of finding unstable ones.
They didn’t set out to do so. In 2021, they used a neural network as a new way to search indiscriminately for singularity candidates of any kind. A neural network is, in general, a function defined by a vast array of numbers. These numbers get carefully adjusted through a highly efficient “training” process of guessing, checking, and refining until the function can perform some desired task. For instance, if you calibrate a neural network using thousands of labeled photos of cats and dogs, it “learns” to take in unlabeled images it’s never seen before and label them “cat” or “dog.”
Buckmaster and his team turned to what’s known as a physics-informed neural network, or PINN. Unlike an image-classifying neural network, a PINN doesn’t learn by studying external data. Instead, it takes a partial differential equation — an equation that describes how a system changes over time — and adjusts itself until it can represent a function that solves that equation. It can, for instance, take fluid equations and train itself to home in on a function that captures a valid history of a fluid, possibly one that contains a singularity.
But no computer technique can directly render the infinite nature of a singularity. Imagine playing the simulation of your fluid and watching it move forward in time. You might represent some quantity, such as the velocity at different points in the fluid, as a curve on a graph. As the fluid changes over time, you’ll see that curve change as well, like a movie. If the curve gets much steeper from one frame to the next, the fluid might be approaching a singularity. The simulation, however, can’t reach that final destination. The computer will run out of memory before the curve gets infinitely steep, crashing the program. Then you can’t know for sure what was going to happen — if you were truly headed for a blowup or not.
To sidestep the inconvenience of infinity, mathematicians have recently focused their search on singularities with a special property called self-similarity. This means that there is a way of stretching the velocity curve in one frame to match the steeper velocity curve in a later frame. And so, if you want to catch a potential singularity, you no longer need to try to watch the curve get infinitely steep. Instead, you can zoom in on the steepening section of the curve while the movie plays in a way that neutralizes the steepening. From this new, dynamic perspective, the curve gets closer and closer to a frozen curve of finite steepness instead. This transformation renders the target — the frozen limit — a finite object that a finite computer can handle.
Buckmaster’s team realized that PINNs could be an extremely efficient way of finding these frozen solutions to fluid equations. Moreover, these neural networks could also determine the unique zoom rate that makes a singular solution appear frozen and finite.
At first, their PINN turned up only known candidates. In 2022, for instance, Buckmaster, Javier Gómez-Serrano of Brown University, and their collaborators used a PINN to home in on the stable blowup that Hou and Luo had found in 2013. (Hou and Chen would prove its existence later that year.)
Tristan Buckmaster (left) and Javier Gómez-Serrano are using neural networks to look for extremely subtle ways of making fluid equations glitch.
Dan Komoda/ Institute for Advanced Study; Jason Rossi/Brown University
They also rediscovered a known singularity candidate in the Córdoba-Córdoba-Fontelos (CCF) equations, which describe a simpler one-dimensional fluid. That singularity candidate was especially notable — it was unstable. It had been found in 2019 because the CCF equations happen to be closely related to an even simpler fluid model that’s well understood. But the PINN could find this solution in a more general way, and much more precisely. That’s because it wasn’t a simulation in the traditional sense, stepping a fluid forward in time. Rather, it went after the frozen limit directly.
“There’s no time, so you don’t care that it’s unstable,” Buckmaster said. “You just try to solve the [equation] itself.”
A New Stable of Instability
Buckmaster and Gómez-Serrano were excited by the prospect of using their PINN to find new unstable singularity candidates. They teamed up with Google DeepMind and spent the next few years fine-tuning the neural network approach to look for unstable blowups in a few different classical fluid theories. Yongji Wang, now a researcher at DeepMind, led the team in switching from off-the-shelf PINNs to bespoke neural networks tailored to fit the specific fluid equations they were trying to solve. The researchers also further tuned the structure of the PINNs to guide them toward solutions with features they knew the singularities should have.
As they did so, their PINNs got better at spotting singularity candidates. A lot better.
In September, their collaboration of more than 20 researchers unveiled a host of singularities that had never been seen before, most of them unstable.
Revisiting the spinning fluid in a can, they described a collection of four new unstable singularity candidates in the Euler equations. These were still broadly similar to Hou and Luo’s known stable singularity, though the initial spinning conditions differed slightly in intensity and other variables. Each candidate they found was more unstable than the last — disappearing even more easily when the setup was tweaked in subtle ways.
They also looked at equations describing how a fluid filters through an incompressible porous medium, such as soil or rock, in two dimensions. No one had ever found singularity candidates in this setup. They found four — one stable, three unstable. All involved a similar setup that can be visualized in a thought experiment, although in reality no scientist would be able to adjust the fluid with the endless precision necessary to make the experiment a reality. Imagine an ant farm filled with a sand layer and a rock layer (but no ants). Now add a blob of water, wetting some of the sand. Over time, gravity pulls the water down through the sand, and the blob flattens as it drops. Eventually it smacks into the rock layer, and a property related to the fluid’s density seems to blow up.
Finally, the team returned to the one-dimensional CCF equations, this time finding an even more unstable singularity than before. One way of visualizing this model is to imagine an expansive puddle with two opposing currents. The CCF equations describe the interface between the two currents. If you put a carefully shaped kink into this interface, it sharpens into a singular cusp.
Notably, like the Navier-Stokes equations (and unlike the other two kinds of equations the researchers studied), the CCF equations describe fluids that have a dissipation property akin to viscosity. Thus, each model they studied shows that the PINN method can handle some challenging aspect of the full Navier-Stokes equations, such as higher dimensions and dissipation.
“We are trying to isolate the technical difficulties one by one,” Gómez-Serrano said.
Crucially, none of these new singularity candidates has been proved. But Gómez-Serrano expects that they can be, because the PINN’s approximations are so precise. And the more precise a candidate is, the easier it is to prove that it’s a true singularity. Compared to when the group first unleashed their PINN a few years ago, they’ve gotten about a billion times more accurate.
“The precision is remarkable,” said Eva Miranda, a mathematician at the Polytechnic University of Catalonia in Spain. “The residual errors are so small that these solutions could realistically be used as seeds for future computer-assisted proofs.”
Race To Escape the Boundary
The million-dollar question, or technically the warm-up question to the million-dollar question, is whether the DeepMind collaboration can now use their PINN machinery to find a singularity in the Euler equations — for a fluid that isn’t trapped in a can, a much harder problem. The mathematicians say they will need to upgrade their techniques once again for this wilder and more complicated fluid, but they’re optimistic.
“You’re building a robust tool to find things that are very hard to find,” Buckmaster said.
Other mathematicians, however, point out that past performance does not guarantee future returns, because an unbounded fluid is nothing like a bounded one. “It’s a completely different animal,” said Diego Córdoba, a mathematician at the Institute of Mathematical Sciences in Spain and one of the Córdobas of the CCF model. (His father is the other.)
And so the competition is heating up as researchers hunt for “boundary-free” singularities in the Euler equations and beyond. Córdoba and his collaborator, Luis Martínez-Zoroa of CUNEF University in Spain, have used pencil-and-paper techniques to discover stable singularities in a handful of different fluid setups. They believe they’re on the verge of getting their approach to work for a boundary-free Euler fluid. (Córdoba had fretted that the DeepMind collaboration was about to beat them to that goal, but to his relief, their PINNs aren’t yet powerful enough to crack the problem. The solutions they’ve found, he said, “are unstable, but not that unstable.”)
Another competitor, Tarek Elgindi of the University of California, San Diego, has already had success working in boundary-free settings (with other caveats) and is intent on extending his strategy’s reach as well.
It’s not clear which technique, if any, will reach the finish line. “I’ll be very proud and very happy if Javi manages to do it,” said Córdoba, who was Gómez-Serrano’s doctoral adviser. “But I’ll be even happier if we manage to do it.”
If someone can, then it will be on to Navier-Stokes. But despite the recent rash of progress in finding new fluid glitches, mathematicians hesitate to raise their hopes too high.
“You may daydream, but only for a day or two,” Gómez-Serrano said. “You don’t have good enough ideas. Then the daydream stops.”
