Simple Set Game Proof Stuns Mathematicians

Olena Shmahalo/Quanta Magazine
Introduction
In a series of papers posted online in recent weeks, mathematicians have solved a problem about the pattern-matching card game Set that predates the game itself. The solution, whose simplicity has stunned mathematicians, is already leading to advances in other combinatorics problems.
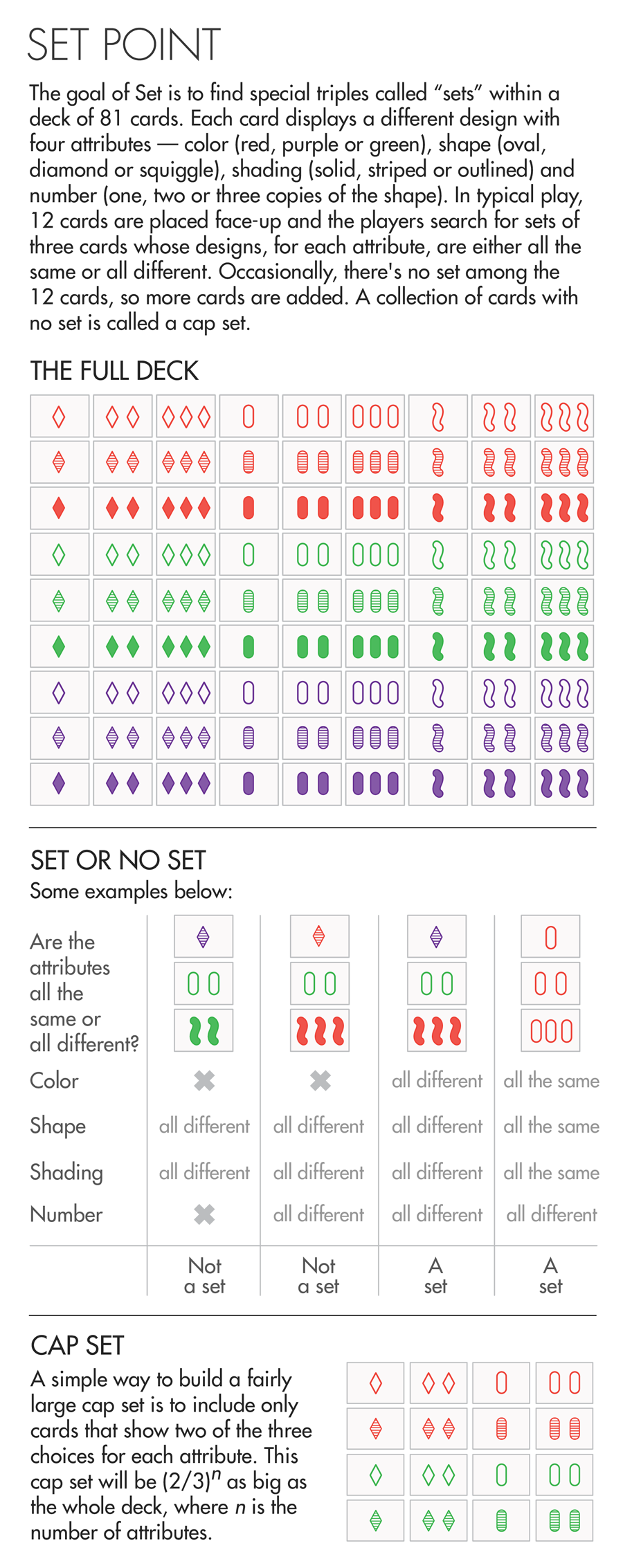
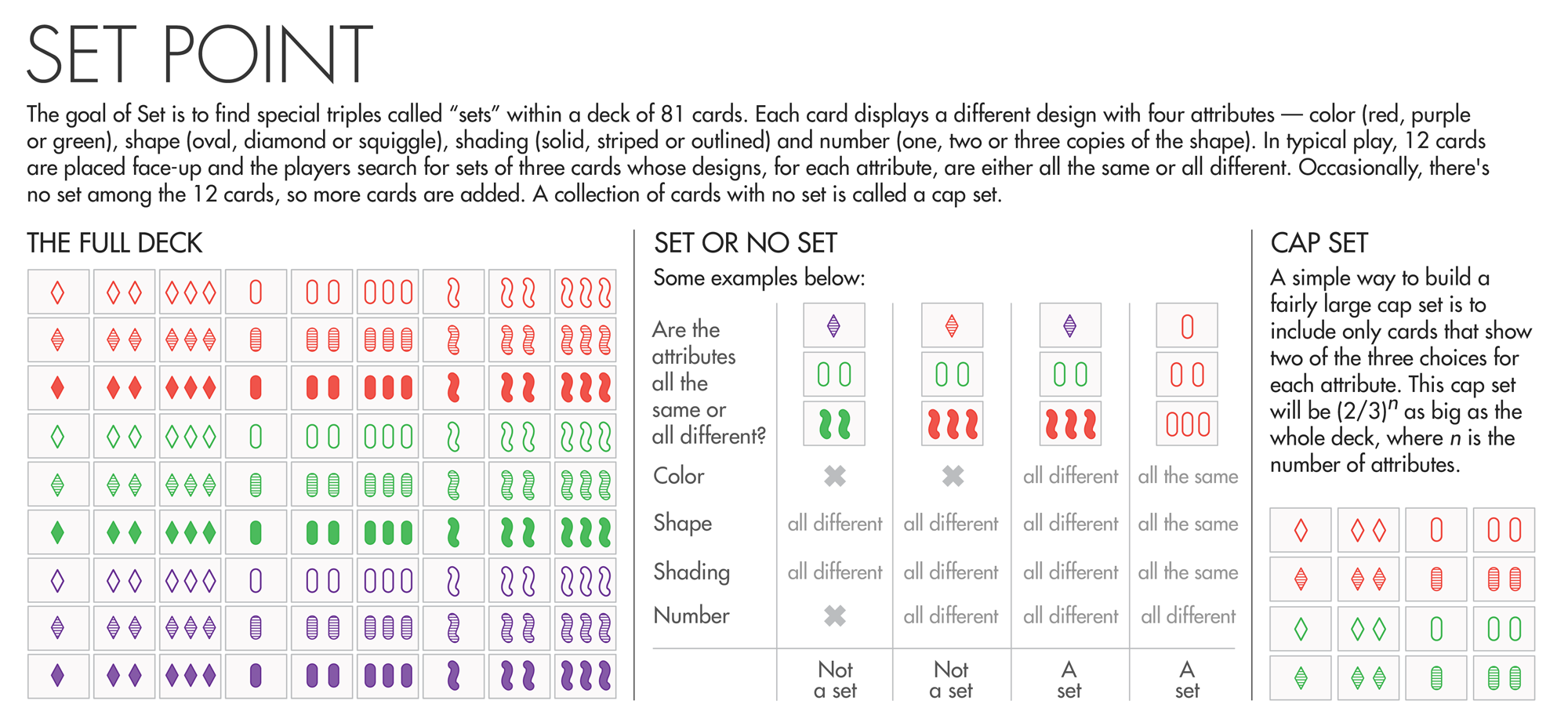
Invented in 1974, Set has a simple goal: to find special triples called “sets” within a deck of 81 cards. Each card displays a different design with four attributes — color (which can be red, purple or green), shape (oval, diamond or squiggle), shading (solid, striped or outlined) and number (one, two or three copies of the shape). In typical play, 12 cards are placed face-up and the players search for a set: three cards whose designs, for each attribute, are either all the same or all different.
Occasionally, there’s no set to be found among the 12 cards, so the players add three more cards. Even less frequently, there’s still no set to be found among the 15 cards. How big, one might wonder, is the largest collection of cards that contains no set?
The answer is 20 — proved in 1971 by the Italian mathematician Giuseppe Pellegrino. But for mathematicians, this answer was just the beginning. After all, there’s nothing special about having designs with only four attributes — that choice simply creates a manageable deck size. It’s easy to imagine cards with more attributes (for instance, they could have additional images, or even play different sounds or have scratch-and-sniff smells). For every whole number n, there’s a version of Set with n attributes and 3n different cards.
For each such version, we can consider collections of cards that contain no set — what mathematicians confusingly call “cap sets” — and ask how large they can be. Mathematicians have calculated the maximal size of cap sets for games with up to six attributes, but we’ll probably never know the exact size of the largest cap set for a game with 100 or 200 attributes, said Jordan Ellenberg, a mathematician at the University of Wisconsin, Madison — there are so many different collections of cards to consider that the computations are too mammoth ever to be carried out.
Yet mathematicians can still try to figure out an upper bound on how big a cap set can be — a number of cards guaranteed to hold at least one set. This question is one of the simplest problems in the mathematical field called Ramsey theory, which studies how large a collection of objects can grow before patterns emerge.
“The cap set problem we think of as a model problem for all these other questions in Ramsey theory,” said Terence Tao, a mathematician at the University of California, Los Angeles, and a winner of the Fields Medal, one of mathematics’ highest honors. “It was always believed that progress would come there first, and then once we’d sorted that out we would be able to make progress elsewhere.”
Yet until now, this progress has been slow. Mathematicians established in papers published in 1995 and 2012 that cap sets must be smaller than about 1/n the size of the full deck. Many mathematicians wondered, however, whether the true bound on cap set size might be much smaller than that.
They were right to wonder. The new papers posted online this month showed that relative to the size of the deck, cap set size shrinks exponentially as n gets larger. In a game with 200 attributes, for instance, the previous best result limited cap set size to at most about 0.5 percent of the deck; the new bound shows that cap sets are smaller than 0.0000043 percent of the deck.
The previous results were “already considered to be quite a big breakthrough, but this completely smashes the bounds that they achieved,” said Timothy Gowers, a mathematician and Fields medalist at the University of Cambridge.
There’s still room to improve the bound on cap sets, but in the near term, at least, any further progress is likely to be incremental, Gowers said. “In a certain sense this completely finishes the problem.”
Game, Set, Match
To find an upper bound on the size of cap sets, mathematicians translate the game into geometry. For the traditional Set game, each card can be encoded as a point with four coordinates, where each coordinate can take one of three values (traditionally written as 0, 1 and 2). For instance, the card with two striped red ovals might correspond to the point (0, 2, 1, 0), where the 0 in the first spot tells us that the design is red, the 2 in the second spot tells us that the shape is oval, and so on. There are similar encodings for versions of Set with n attributes, in which the points have n coordinates instead of four.
The rules of the Set game translate neatly into the geometry of the resulting n-dimensional space: Every line in the space contains exactly three points, and three points form a set precisely when they lie on the same line. A cap set, therefore, is a collection of points that contains no complete lines.
Lucy Reading-Ikkanda for Quanta Magazine
Previous approaches to getting an upper bound on cap set size used a technique called Fourier analysis, which views the collection of points in a cap set as a combination of waves and looks for the directions in which the collection oscillates. “The conventional wisdom was that this was the way to go,” Tao said.
Now, however, mathematicians have solved the cap set problem using an entirely different method — and in only a few pages of fairly elementary mathematics. “One of the delightful aspects of the whole story to me is that I could just sit down, and in half an hour I had understood the proof,” Gowers said.
The proof uses the “polynomial method,” an innovation that, despite its simplicity, only rose to prominence on the mathematical scene about a decade ago. The approach produces “beautiful short proofs,” Tao said. It’s “sort of magical.”
A polynomial is a mathematical expression built out of numbers and variables raised to powers — for instance, x2 + y2 or 3xyz3 + 2. Given any collection of numbers, it’s possible to create a polynomial that evaluates to zero at all those numbers — for example, if you pick the numbers 2 and 3, you can build the expression (x – 2)(x – 3); this multiplies out to the polynomial x2 – 5x + 6, which equals zero if x = 2 or x = 3. Something similar can be done to create polynomials that evaluate to zero at a collection of points — for instance, the points corresponding to Set cards.
At first glance, this doesn’t seem like a very deep fact. Yet somehow, these polynomials often seem to contain information that isn’t readily visible from the set of points. Mathematicians don’t fully understand, Ellenberg said, just why this approach works so well, and which types of problems it can be useful for. Until a few weeks ago, he added, he considered cap set “an example of a problem where the polynomial method really has no purchase.”
That changed on May 5, when three mathematicians — Ernie Croot of the Georgia Institute of Technology, Vsevolod Lev of the University of Haifa, Oranim, in Israel, and Péter Pál Pach of the Budapest University of Technology and Economics in Hungary — posted a paper online showing how to use the polynomial method to solve a closely related problem, in which each Set attribute can have four different options instead of three. For technical reasons, this problem is more tractable than the original Set problem.
In this game variant, for any collection of cards with no set, Croot, Lev and Pach considered which additional cards could be laid down on the table to complete a set. They then built a polynomial that evaluates to zero on these completion cards, and figured out an ingeniously simple way to split the polynomial into pieces with smaller exponents, which led to a bound on the size of collections with no sets. It was a “very inventive move,” Ellenberg said. “It’s always incredibly cool when there’s something truly new and it’s easy.”
The paper soon set off a cascade of what Ellenberg called “math at Internet speed.” Within 10 days, Ellenberg and Dion Gijswijt, a mathematician at Delft University of Technology in the Netherlands, had each independently posted papers showing how to modify the argument to polish off the original cap set problem in just three pages. Yesterday, they posted a joint paper combining their results. The trick, Ellenberg said, is to realize that there are many different polynomials that evaluate to zero on a given set of points, and that choosing just the right one gets “a little bit more juice out of the method.” A cap set, the new proofs establish, can be at most (2.756/3)n as large as the whole deck.
Mathematicians are now scrambling to figure out the implications of the new proof. Already, a paper has been posted online showing that the proof rules out one of the approaches mathematicians were using to try to create more efficient matrix multiplication algorithms. And on May 17, Gil Kalai, of the Hebrew University of Jerusalem, wrote an “emergency” blog post pointing out that the cap set result can be used to prove the “Erdős-Szemerédi sunflower conjecture,” which concerns sets that overlap in a sunflower pattern.
“I think a lot of people will be thinking, ‘What can I do with this?’” Gowers said. Croot, Lev and Pach’s approach, he wrote in a blog post, is “a major new technique to add to the toolbox.”
The fact that the cap set problem finally yielded to such a simple technique is humbling, Ellenberg said. “It makes you wonder what else is actually easy.”
This article was reprinted on Wired.com.