What's up in
Abstractions blog
Latest Articles
How Computationally Complex Is a Single Neuron?
Computational neuroscientists taught an artificial neural network to imitate a biological neuron. The result offers a new way to think about the complexity of single brain cells.
The Complex Truth About ‘Junk DNA’
Genomes hold immense quantities of noncoding DNA. Some of it is essential for life, some seems useless, and some has its own agenda.
To Learn More Quickly, Brain Cells Break Their DNA
New work shows that neurons and other brain cells use DNA double-strand breaks, often associated with cancer, neurodegeneration and aging, to quickly express genes related to learning and memory.
Banach-Tarski and the Paradox of Infinite Cloning
One of the strangest results in mathematics explains how it’s possible to turn one sphere into two identical copies, simply by rearranging its pieces.
Computer Scientists Discover Limits of Major Research Algorithm
The most widely used technique for finding the largest or smallest values of a math function turns out to be a fundamentally difficult computational problem.
Physicists Create a Bizarre ‘Wigner Crystal’ Made Purely of Electrons
The unambiguous discovery of a Wigner crystal relied on a novel technique for probing the insides of complex materials.
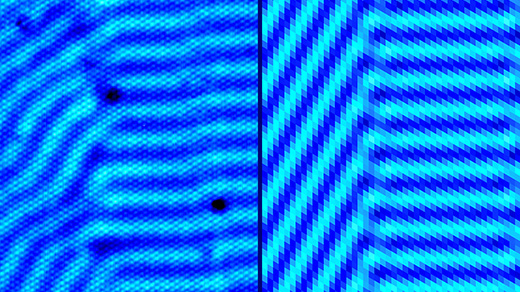
Turing Patterns Turn Up in a Tiny Crystal
The mechanism behind leopard spots and zebra stripes also appears to explain the patterned growth of a bismuth crystal, extending Alan Turing’s 1952 idea to the atomic scale.
Neither Star nor Planet: A Strange Brown Dwarf Puzzles Astronomers
Brown dwarfs such as “The Accident” are illuminating the murky borderlands that separate planets from stars.
Galois Groups and the Symmetries of Polynomials
By focusing on relationships between solutions to polynomial equations, rather than the exact solutions themselves, Évariste Galois changed the course of modern mathematics.