Computer Scientists Combine Two ‘Beautiful’ Proof Methods

Kristina Armitage/ Quanta Magazine
Introduction
How do you prove something is true? For mathematicians, the answer is simple: Start with some basic assumptions and proceed, step by step, to the conclusion. QED, proof complete. If there’s a mistake anywhere, an expert who reads the proof carefully should be able to spot it. Otherwise, the proof must be valid. Mathematicians have been following this basic approach for well over 2,000 years.
Then, in the 1980s and 1990s, computer scientists reimagined what a proof could be. They developed a dizzying variety of new approaches, and when the dust settled, two inventions loomed especially large: zero-knowledge proofs, which can convince a skeptic that a statement is true without revealing why it is true, and probabilistically checkable proofs, which can persuade a reader of the truth of a proof even if they only see a few tiny snippets of it.
“These are, to me, two of the most beautiful notions in all of theoretical computer science,” said Tom Gur, a computer scientist at the University of Cambridge.
It didn’t take long for researchers to try combining these two types of proof. They won a partial victory in the late 1990s, using lesser versions of each condition. For decades, no one could merge the ideal version of zero knowledge with the ideal version of probabilistic checkability.
Until now. In a paper that marks the culmination of seven years of work, Gur and two other computer scientists have finally combined the ideal versions of the two kinds of proof for an important class of problems.
“It’s a very important result,” said Eli Ben-Sasson, a theoretical computer scientist and founder of the company StarkWare, which develops cryptographic applications of zero-knowledge proofs. “It solves a very old and well-known open problem that has baffled researchers, including myself, for a very long time.”
Check, Please
The story begins in the early 1970s, when computer scientists began to formally study the difficulty of the problems they were asking computers to solve. Many of these problems share an important property: If someone finds a valid solution, they can easily convince a skeptical “verifier” that it really is valid. The verifier, in turn, will always be able to spot if there’s a mistake. Problems with this property belong to a class that researchers call NP.
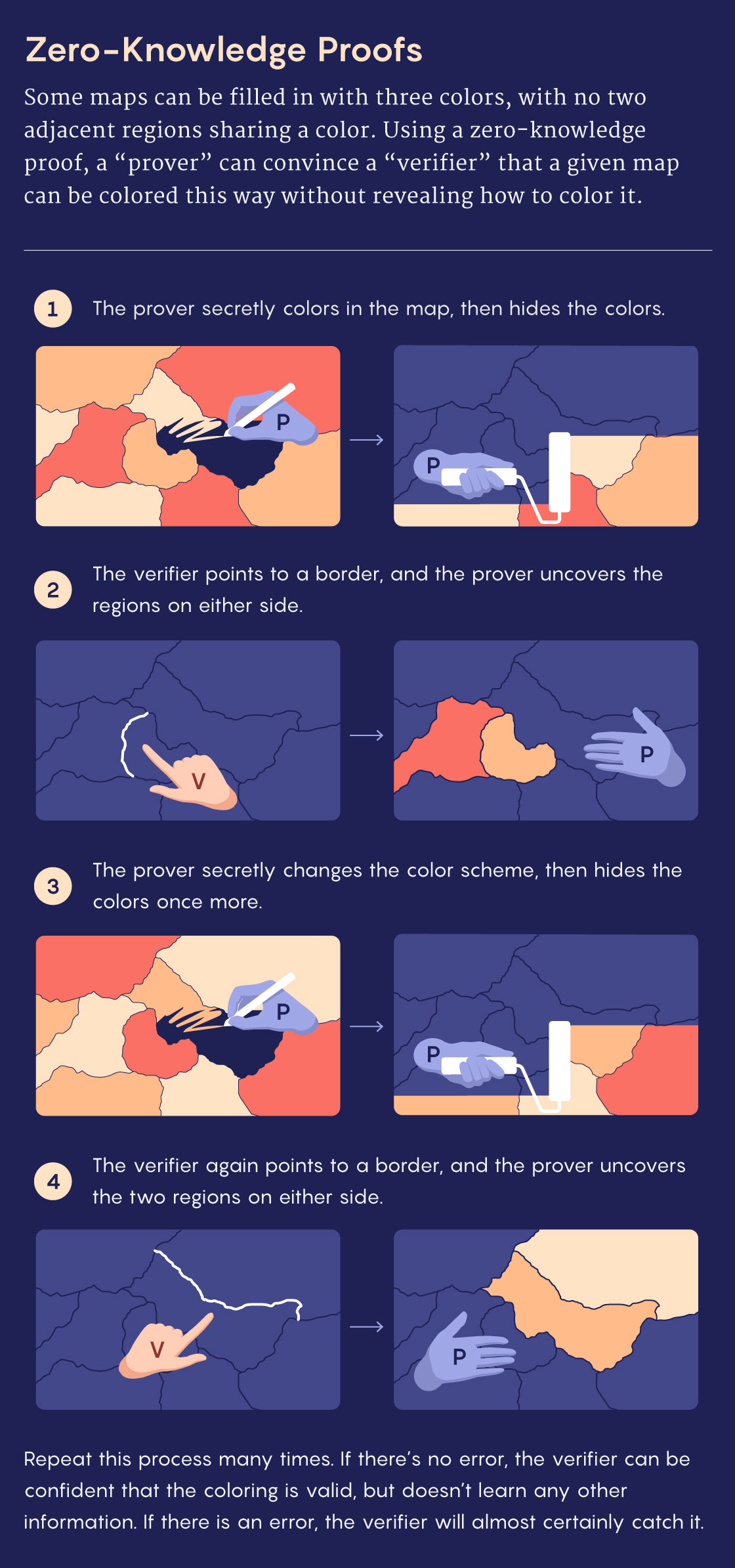
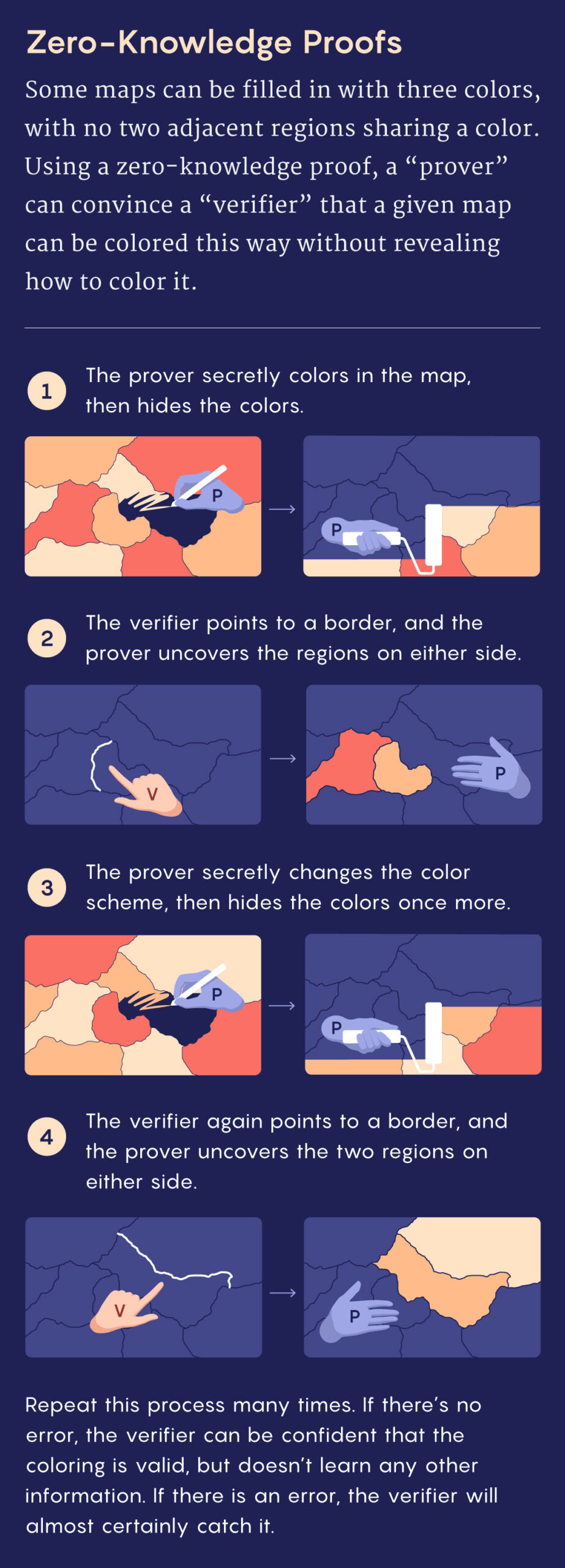
To understand how such verification can work, consider this classic NP problem: Given a map divided into different regions, is it possible to fill it in using just three colors without giving adjacent regions the same color? Depending on the map, this problem can be notoriously difficult. But if you manage to find a valid coloring, you can prove it by showing a verifier a properly colored map. The verifier just needs to glance at every border.
A decade later, two graduate students pioneered a different way to think about mathematical proof. Shafi Goldwasser and Silvio Micali, both at the University of California, Berkeley, had been wondering whether it was possible to prevent cheating in an online poker game. That would require somehow proving that the cards in each player’s hand were drawn randomly, without also revealing what those cards were.
Goldwasser and Micali answered their own question with a resounding yes by inventing zero-knowledge proofs in a seminal 1985 paper, co-authored with the University of Toronto computer scientist Charles Rackoff. The following year, Micali and two other researchers followed up with a paper showing that the solution to any problem in NP can be verified using a specific kind of zero-knowledge proof.
To get a sense of these proofs, suppose that you once again want to convince a verifier that a particular map is three-colorable — but this time, you don’t want the verifier to learn how to color it themself. Instead of drawing an example, you can prove it through an interactive process. Start by coloring in the map, and then carefully cover every region with black tape, leaving only the borders visible. The verifier then picks a border at random, and you’ll uncover the regions on either side, revealing two different colors.
Now repeat this process many times, randomly switching up the color scheme before each round so that the verifier can’t piece together any consistent information about your solution. (For example, swap red and blue regions and leave green regions unchanged.) If you’re bluffing, the verifier will eventually find a spot where the map isn’t properly colored. If you’re telling the truth, you’ll be able to convince them beyond a reasonable doubt in about as much time as it would take to verify a proof using the standard approach.
Mark Belan/Quanta Magazine
This zero-knowledge proof is strikingly different from the standard approach in two ways: It’s an interactive process rather than a document, and each participant relies on randomness to ensure that the other can’t predict their decisions. But because of that randomness, there’s now always a chance that a flawed proof will be deemed valid. Still, it’s easy to make that probability extremely small, and computer scientists quickly got over their discomfort at this looser definition of proof.
As Amit Sahai, a computer scientist at the University of California, Los Angeles, put it, “If the chance that something is not correct is less than one out of the number of particles in the universe, it seems reasonable for us to call that a proof.”
Pretty Cool Proofs
Researchers soon realized that randomized interactive proofs could do more than just hide secret information. They also enabled easy verification for problems much harder than those in NP. One type of interactive proof even worked for all problems in a class called NEXP. With ordinary proofs, the solutions to these problems can take as long just to verify as the hardest NP problems take to solve.
The proof revolution culminated in one final surprising discovery: You can still get the full power of interactive proofs without any interactions.
In principle, removing interactivity is straightforward. “The prover lists out all the possible challenges he could ever get from the verifier, and then just writes out all of his answers ahead of time,” Sahai said. The catch is that for complicated problems like the hardest ones in NEXP, the resulting document would be enormous, far too long to read from start to finish.
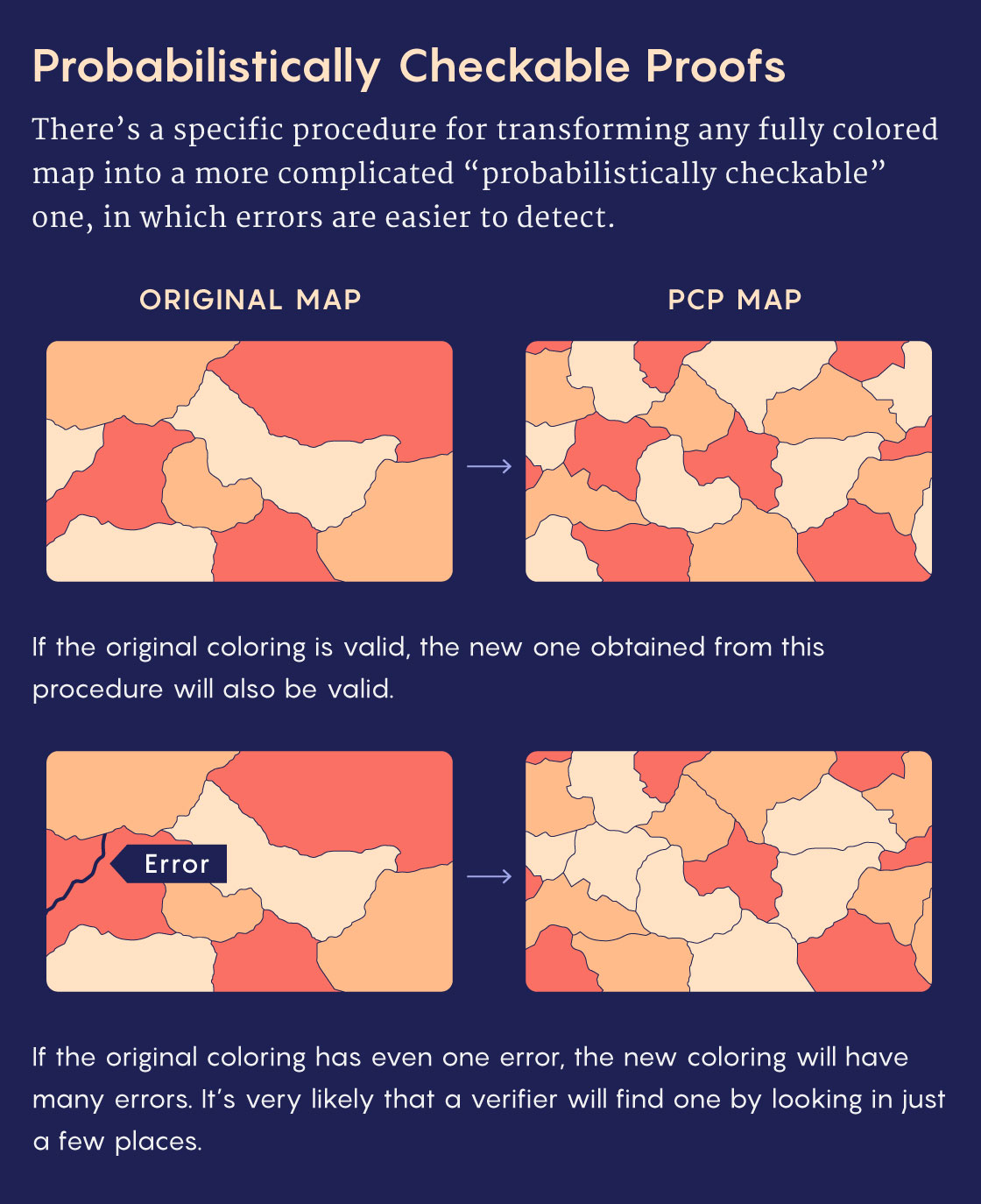
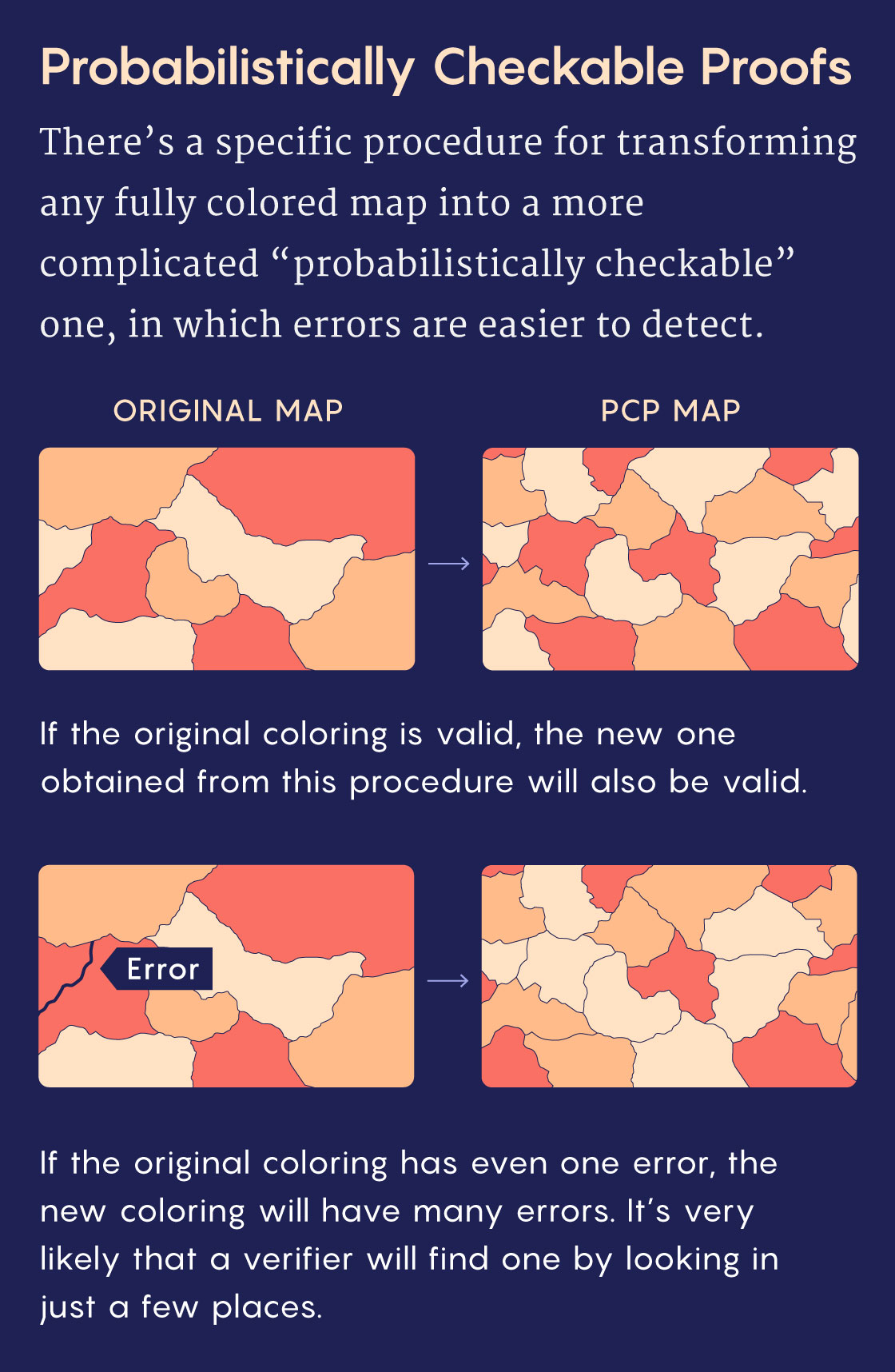
Then in 1992, the computer scientists Sanjeev Arora and Shmuel Safra defined a new class of noninteractive proofs: probabilistically checkable proofs, or PCPs. Along with other researchers, they showed that any solution to a NEXP problem could be rewritten in this special form. While PCPs are even longer than ordinary proofs, they can be rigorously vetted by a verifier who only reads small snippets. That’s because a PCP effectively multiplies and distributes any error in an ordinary proof. Trying to find an error in a normal proof is like hunting for a tiny dollop of jam by nibbling on a slice of toast. A PCP “spreads the jam uniformly over the piece of bread,” Gur said. “Wherever you take a bite, it doesn’t matter, you will always find it.”
Mark Belan/Quanta Magazine
The crucial element was, again, randomness — the verifier’s choice of snippets would have to be unpredictable, to ensure that a dishonest prover couldn’t hide inconsistencies anywhere.
Arora, Safra and others showed that PCPs could also dramatically speed up verification for more common NP problems. Soon after, Arora and four other researchers improved PCPs further, pushing the speed of NP proof verification to a theoretical limit — a celebrated result known as the PCP theorem.
“This is considered one of the big achievements of theoretical computer science,” said Yuval Ishai, a cryptographer at the Technion in Haifa, Israel.
The road to the PCP theorem had been anything but straightforward. Researchers started with zero-knowledge proofs for NP problems that used both interactivity and randomness. Then they realized that similar proofs could be used to verify the solutions to far harder problems. Finally, they showed that by transforming those proofs into noninteractive PCPs, they could verify a solution in less time than it would take to just read the proof. Computer scientists were feeling triumphant.

In the 1990s, Sanjeev Arora and other researchers figured out how to construct probabilistically checkable proofs, which verifiers can vet by reading just a few snippets.
Silvia Weyerbrock
In the years that followed, though, some researchers began to consider what had been lost along the way. It turned out that transforming proofs into PCPs exposed some of the information that zero-knowledge proofs were designed to conceal. Was there any way to get the best of both worlds?
Too Much Information
Unfortunately, there’s an inherent tension between probabilistic checkability and zero knowledge. The trouble begins with the noninteractive nature of PCPs. Ordinary zero-knowledge proofs rely on interactivity to restrict the verifier’s access to private information. A noninteractive proof is just a document that the prover hands over to the verifier, who might care more about stealing the prover’s secrets than about vetting the solution.
“It’s not as simple as trying to disguise what they’re supposed to look at,” said Jack O’Connor, a graduate student at Cambridge who worked with Gur on the new result. “We have to disguise it regardless of how they inspect the proof.”
It’s impossible to achieve zero knowledge with a proof that a verifier can simply read from start to finish (unless you assume that specific kinds of encryption are unbreakable). Instead, researchers focused on crafting zero-knowledge versions of PCPs for the ultrahard problems beyond NP, since these PCPs are verifiable despite being too long to read in their entirety. The zero-knowledge versions would have to spread information through every part of the proof to keep the prover honest, yet somehow prevent the proof from revealing anything other than its correctness, no matter which snippets the verifier reads.
In 1997, three researchers overcame these challenges and constructed a type of zero-knowledge PCP that worked for any problem in NEXP — but at a cost. They had to add a whiff of interactivity back into how the verifier vets the proof — a departure from the usual situation where there’s nothing interactive about a PCP.
“You go and look at it first, then you think about it, and then you go back to it and read another part,” Sahai said. With an ordinary PCP, “you could just decide at the beginning what small portion of the proof you want to read.”
The result also used a form of zero knowledge that fell short of the ideal, since there was a tiny but nonzero chance that the verifier could learn some extra information. This is good enough for all practical applications of zero-knowledge proofs in cryptography. But some researchers can’t resist the allure of “perfect zero knowledge” — a demanding condition that’s not always possible, even with interactive proofs.
Absolute Zero
Over the next 20 years, a handful of researchers refined the methods in the 1997 paper, making zero-knowledge PCPs more useful in cryptographic applications. But the fundamental limitations remained. Then in 2017, a Berkeley graduate student named Nicholas Spooner (who’s now at Cornell University) began to suspect that techniques he’d helped develop for a related problem might also be useful for building perfect zero-knowledge PCPs.
Spooner pitched the idea to Gur, who was then a postdoc at Berkeley. Gur wasn’t convinced, and he spent the next year trying to prove that it couldn’t be done. But he changed his mind one morning in a Berkeley café, after Spooner showed him a simple trick that eliminated the most obvious obstacle to the new approach.


Clockwise from left: Tom Gur, Jack O’Connor and Nicholas Spooner built proofs that combined the ideal version of zero knowledge with the ideal version of probabilistic checkability
Photos courtesy of Eynat Gur (top right), Melanie Cheung (left), and Helen Oleynikova
From left: Tom Gur, Jack O’Connor and Nicholas Spooner built proofs that combined the ideal version of zero knowledge with the ideal version of probabilistic checkability.
Photos courtesy of Eynat Gur (left), Melanie Cheung (middle) and Helen Oleynikova.
“I was a bit of a pessimist, he was more of an optimist,” Gur said. “He won.”
The two researchers focused on “counting problems” about the number of solutions to NP problems, such as, “Given a map, how many distinct valid colorings are possible?” There’s a standard recipe for constructing PCPs for such problems using giant multidimensional tables of numbers, in which a verifier can add together certain entries to learn the answer, and add up others to check that the prover stays honest. But the values of the individual numbers reveal extra information, so these PCPs aren’t zero-knowledge. In Spooner’s new approach, the prover would hide those values by adding randomness into the table, and the verifier would be able to check that this randomness didn’t distort the final sum.
Gur and Spooner worked together on and off for over five years, but they couldn’t get the details to work out. O’Connor joined the team in 2023, after the trio realized that the key missing ingredient might be found in a seemingly unrelated paper they’d worked on together. After one final concerted effort in the fall, the three researchers put all the pieces together in their new paper. The result was a perfect zero-knowledge PCP for all counting problems. What’s more, the verification process for those PCPs was also totally noninteractive.
“They break through two barriers at once,” Ishai said. “I was highly impressed.”
The counting problems that Spooner, Gur and O’Connor studied belong to a class of problems called #P (pronounced “sharp P”), which lies between NP and NEXP in terms of difficulty. The three researchers now aim to extend their new technique to apply to all problems in NEXP, matching the power of the PCPs in Arora and Safra’s original paper. That would be a big step toward proving something analogous to the original PCP theorem, but with perfect zero knowledge as an added benefit. Gur is optimistic, because their new method amounts to a zero-knowledge version of a technique that played a key role in the PCP theorem.
New proof methods often have applications in other branches of computer science — another reason that researchers are excited about the new work.
“It is very likely to revive the interest in zero-knowledge PCPs,” Ishai said. “This might lead to other advances in theoretical computer science.” Proofs, once again, are proving full of surprises.



