Math Patterns That Go On Forever but Never Repeat

Robert Neubecker for Quanta Magazine
Introduction
Have you ever admired how the slats of a hardwood floor fit together so cleanly, or how the hexagons underneath your bathroom rug perfectly meet up? These are examples of geometric tilings, arrangements of shapes that fit snugly together while filling up space. Two-dimensional tilings are admired all around the world, both for their beauty — as seen in the artistry of mosaics in cathedrals and mosques around the world — and for their utility, in walls and floors everywhere.
In math, tilings are often appreciated for their regular patterns. But mathematicians also find beauty in irregularity. It’s this kind of beauty that a retired print technician was seeking when he recently discovered the first “aperiodic monotile”— a single tile that fills up the plane in a non-repeating pattern. To get a handle on this big discovery, let’s start by thinking about a simpler problem: how to tile a line.
Let’s imagine our line-filling tiles to be letters that stick together to form sequences. If the tiles and the rules we adopt for placing them allow us to create a string of letters that goes on infinitely in both directions, we can “tile the line.” For example, let’s say we have two tiles, A and B, and two rules for putting them together:
- Next to an A, on either side you can only place a B.
- Next to a B, on either side you can only place an A.
Can we tile the line with these tiles and these rules? Absolutely. Suppose we put an A down first.
A
According to the rules, we must put B’s on either side.
BAB
Now, on either side of these B’s, we must put A’s, and so on.
…ABABABABABABA…
With these tiles and rules, we can continue forever in both directions, so we can tile the line. In fact, we can draw a stronger conclusion: This is essentially the only way we can tile the line with these rules. Let’s see what that means.
Suppose instead we started with B.
B
The rules require that we put A’s on either side.
ABA
And then B’s on either side of the A’s, and so on.
…BABABABABABAB…
This looks like a second valid tiling of the line. But let’s compare it side by side with the first.
…BABABABABABAB…
…ABABABABABABA…
If we slide either tiling over by one tile, the two match up perfectly — forever.
…BABABABABABAB…
…ABABABABABABA…
In other words, after a translation, the tilings are equivalent. This shows that the two tilings follow the same pattern.
A closer look reveals something even more interesting. Start with two copies of the original tiling:
…ABABABABABABA…
…ABABABABABABA…
Now, watch what happens when you slide the top one over two tiles:
…ABABABABABABA…
…ABABABABABABA…
The original tiling matches up with itself. When a tiling is equivalent to itself after a translation, it has “translational symmetry.” (This is like an object having “reflective symmetry” if its two mirror-image halves can be reflected onto each other.)
Translational symmetry shows how a tiling is really just one pattern repeated over and over. In this case, the tiling of the line …ABABABABABABA… can be thought of as infinitely many translated copies of the two-tile pattern AB.
AB
ABAB
ABABAB
This is one simple example of a tiling of the line that has translational symmetry. In two dimensions, there are many familiar examples of tilings of the plane that have this property as well.


In each case above, it’s possible to translate the entire tiling by some amount so that it matches up exactly with the original.


Like our tiling of the line, these two-dimensional tilings with translational symmetry can be thought of as one pattern that repeats over and over. For example, the single hexagon extends in every direction.


To see this in the equilateral-triangle tiling, imagine the triangles coming together to form hexagons, and those hexagons repeating over and over by translation.
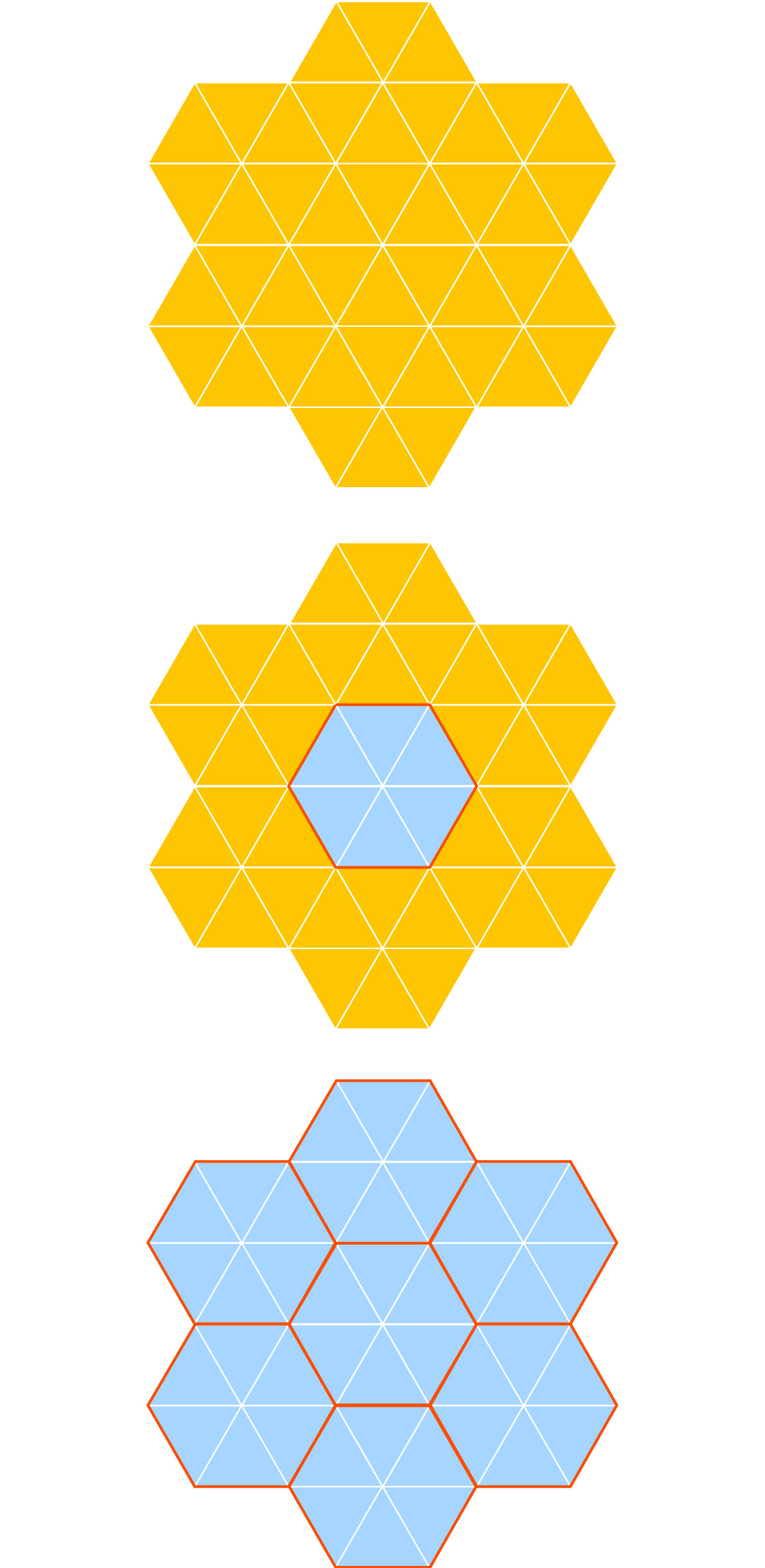

The triangle, hexagon and square tilings of the plane are all “monohedral,” as they’re all composed of infinitely many copies of a single tile. There are also many ways to tile the plane using multiple tiles, as shown below (and on many bathroom floors).


But let’s get back to tiling the line. There’s an important distinction we need to make.
Consider the following new rules for our tiles A and B.
- Next to an A, on either side you can place an A or a B.
- Next to a B, on either side you can only place an A.
Can we still tile the line with these rules? An easy way to see that the answer is yes is to notice that the previous tiling also satisfies the new rule set.
…ABABABABABABA…
But the new rules allow more flexibility, and this leads to more tilings of the line.
For example, these are both valid configurations under the new rules:
AAABABA
ABABAAABAAB
And these can be extended infinitely in either direction in infinitely many ways.
In addition to giving us lots of new tilings of the line, the new rules allow us to generate tilings that, unlike our first example, don’t repeat. For example, consider the following tiling:
…ABAABAAABAAAAB…
What’s the pattern here? Start with an A, then place a B to the right, then two A’s on the right, then a B, then three A’s, then a B, then four A’s, and so on. On the left, just keep adding A’s:
…AAAAAABAABAAABAAAABAAAAAB…
Do this, and you’ll end up with a tiling that can’t be translated onto itself so that everything matches up.
A simple way to see this is to observe that there is a unique leftmost B in this tiling, so where will it go after translation? If you translate to the left, there’s no B for it to match up with. But if you translate to the right, there’s no B coming from the left to match up with it.
The new rules therefore allow both tilings that have translational symmetry and tilings that don’t. There are tilings of the plane that work like this, too.
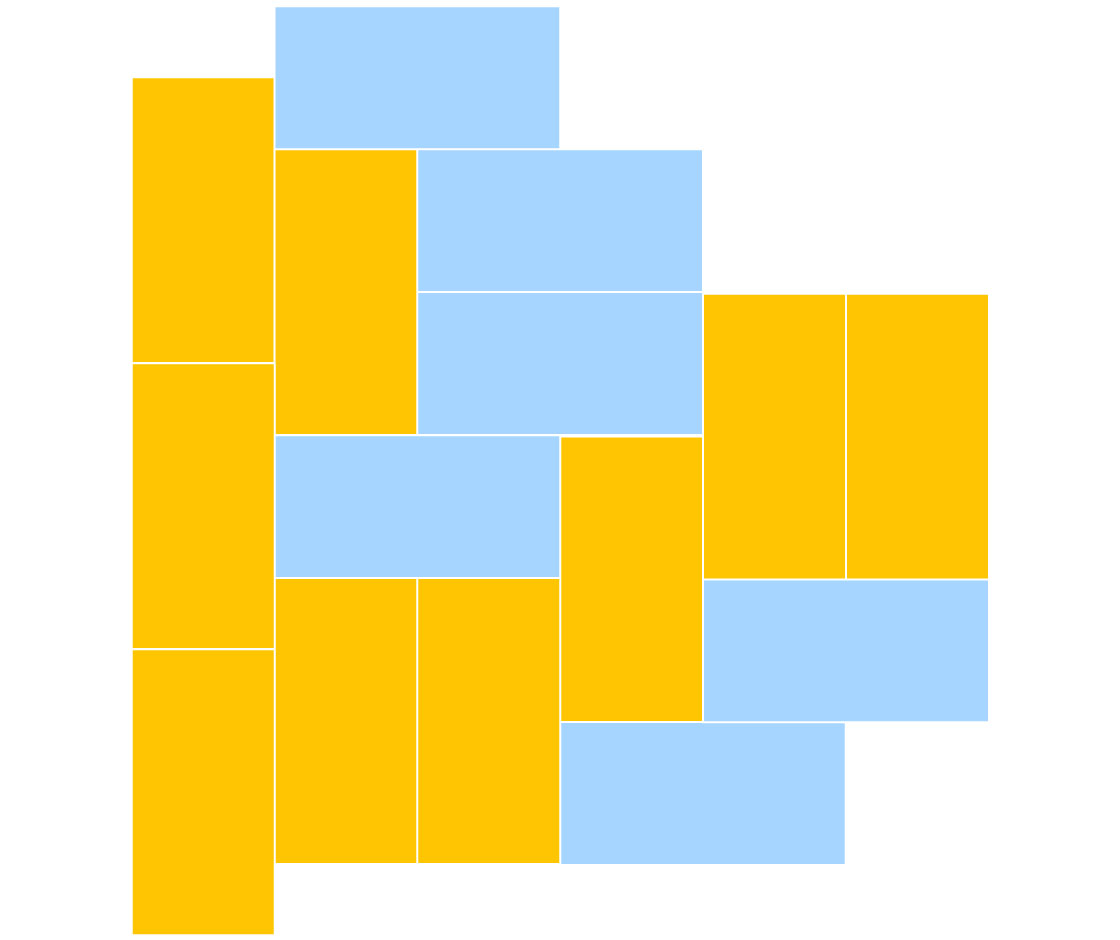
For example, we’ve already seen a tiling with squares that has translational symmetry. By sliding the squares around, we can disrupt some of that translational symmetry.


And with some tiles it’s possible to avoid translational symmetry entirely. Using 2 x 1 rectangles, you can tile the plane in a way so that no translational symmetry emerges at all.

This is a very different situation from the monohedral tilings that use regular hexagons. In those tilings, the repetitive structure is unavoidable. The geometry of the tiles themselves forces the tiling to have translational symmetry. We call such tilings “periodic.”
In contrast, some tiles allow for patterns that repeat and patterns that don’t. This leads to a natural, irresistible question for mathematicians: If there are tilings of the plane that are forced to have this repetitive structure, are there tilings that are forced to avoid it? With this question, formulated in the 1960s, the hunt for “aperiodic tilings” was on.
For our search, we’ll make one more trip back to the line. Our final tiling of one-dimensional space will use an unusual-looking set of tiles:
A-tiles: A, AA, AAA, AAAA, …
B-tiles: B, BB, BBB, BBBB, …
Notice that this tile set is infinite. If this seems like cheating, you’re thinking like a mathematician. We’ll come back to that later, but for now, here are the two rules for putting our infinitely many tiles together:
- Next to an A-tile of length n, you can only put a B-tile of length n on either side.
- Next to a B-tile of length n, you can only put an A-tile of length n + 1 on either side.
As always, our question is: Can we tile the line with these tiles and rules? Well, suppose we start with an A-tile of length 1.
A
The rules dictate that on either side we can only put B-tiles of length 1.
BAB
Now, next to each B we must put A-tiles of length 2.
AABABAA
Then we add B-tiles of length 2.
BBAABABAABB
And so on. It’s easy to see we can go on forever in either direction, which means we can indeed tile the line with these new tiles and rules. And relevant to our search, this tiling does not have translational symmetry. Notice that the single A we placed at the start gets immediately surrounded by B’s on either side, and the resulting pattern — BAB — will never appear again. In the infinitely long string that represents our tiling, every other A that appears will be next to at least one other A. This means there’s nowhere for the BAB string to go, so there’s no way to translate this tiling onto itself.
This will be true regardless of what tile we start with. If it’s B, the rules immediately lead to the string
…BBAABAABB…
And, as before, the pattern ABA will never repeat. Even if you start with something like AAA, the same thing will happen.
…AAAABBBAAABBBAAAA…
Whatever you start with, the initial tile will always be the only A- or B-tile of that particular length, which will prevent any translational symmetry from emerging. This happens to be exactly what we were looking for: a set of tiles and rules that allows us to tile the line but will never allow translational symmetry.
You might be unsatisfied with an aperiodic tiling that requires infinitely many tiles, and you wouldn’t be alone. When mathematicians started seriously looking for aperiodic tilings of the plane, they wanted to find a finite set of tiles that could tile the plane but couldn’t have translational symmetry. An early solution used 20,426 tiles, but within a few years mathematicians had brought that number down to six.
A breakthrough occurred in the 1970s when Roger Penrose, the British mathematician and physicist, discovered the famous two-tile set that now bears his name. Penrose tiles are a pair of simple quadrilaterals that, with a careful set of rules, tile the plane without allowing translational symmetry.

There’s only one way to improve upon a two-tile aperiodic tiling, so mathematicians, hobbyists and artists began searching for an aperiodic “monotile” that would do the job all by itself.
Last November, David Smith found it. This is the “hat,” the first known aperiodic monotile.

Smith, a recreational mathematician, artist and tiling enthusiast, discovered the hat the way much mathematics is discovered: by playing around and seeing what happened. Smith would later connect with the researchers Craig Kaplan, Chaim Goodman-Strauss and Joseph Samuel Myers, who together verified that this was indeed the long-sought aperiodic monotile.
Proving something can tile the plane but can’t have translational symmetry is no easy task, but some of the techniques they used are hinted at in our simple examples. For instance, one way to show that equilateral triangles can tile the plane is to notice that they come together to form larger structures, in this case hexagons, which are known to tile the plane. The hat tile also comes together to form larger, regular structures, which can be used to understand how it tiles the plane.
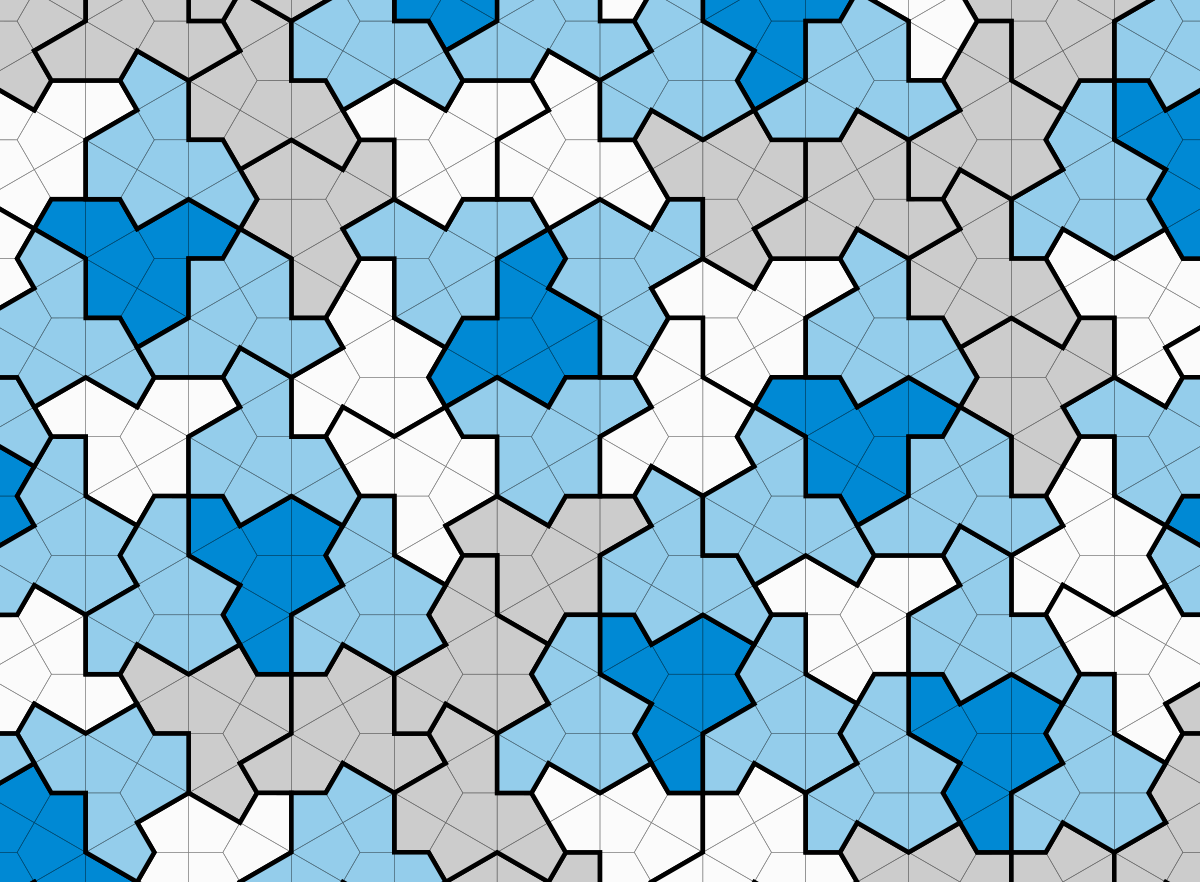
Courtesy of Craig S. Kaplan
While there may be no repeating pattern in our aperiodic tiling of the line, there is a pattern that expands as you move to the right. First you see AB, then AABB, then AAABBB, then AAAABBBB, and so on. This is a kind of self-similarity — a pattern that repeats at changing scales — which can sometimes be used to show that a particular tiling can’t translate onto itself, because doing so would distort length.
Working together, the group proved that using only the hat tile and its mirror image, you can tile the plane, but not with translational symmetry. And unlike other attempts with different tile sets, this one required no special rules. The tile itself forced the aperiodicity. As they got deeper into the geometry, they discovered even more solutions. The hat is actually one of an infinite family of aperiodic tiles!
The search for an aperiodic monotile appears to have come to an end. Or has it? When tiling the plane aperiodically with the hat, you also need its reflection (what you get if you flip the tile over). Maybe there’s a yet-undiscovered aperiodic monotile out there that doesn’t require its mirror image. Find it and you’ll be famous. The inspiration might be right under your feet.
Correction: May 23, 2023
This column has been revised to reflect the fact that a repetitive structure is avoidable in monohedral tilings of equilateral triangles.
Correction: May 29, 2023
The column was further revised to clarify that by sliding square tiles around, we can disrupt translational symmetry in one direction.



