Mathematicians Cut Apart Shapes to Find Pieces of Equations

If you have two flat paper shapes and a pair of scissors, can you cut up one shape and rearrange it as the other? If you can, the shapes are “scissors congruent.”

But, mathematicians wonder, can you tell if two shapes share this relationship even without using scissors? In other words, are there characteristics of each shape you could measure ahead of time to determine whether they’re scissors congruent?

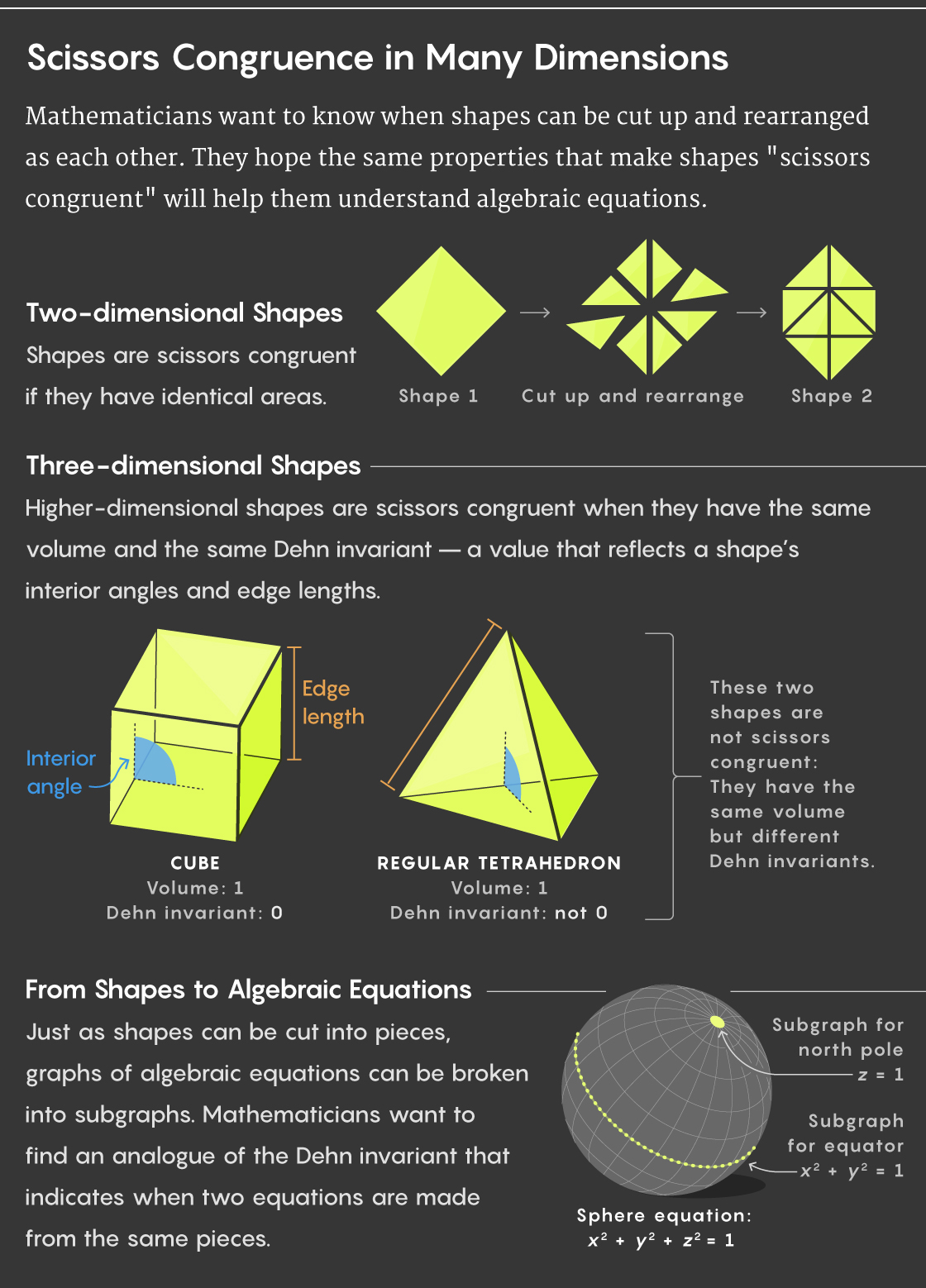
For two-dimensional shapes, the answer is easy: Just determine their areas. If they’re the same, the shapes are scissors congruent.

But for higher-dimensional shapes — like a three-dimensional ball, or an 11-dimensional doughnut that’s impossible to picture — the question of cutting one up and reassembling it as another is a lot harder. Despite centuries of effort, mathematicians have been unable to identify characteristics that dictate scissors congruence for most higher-dimensional shapes.

This fall, however, two mathematicians made the most significant headway on the problem in decades. In a paper presented at the University of Chicago on Oct. 6, Jonathan Campbell of Duke University and Inna Zakharevich of Cornell University took a substantial step toward proving scissors congruence for shapes of any dimension.

But they did more than that. Like all important problems in mathematics, scissors congruence is a rabbit hole: a modest statement that draws mathematicians into a warren of sophisticated mathematics. In their effort to understand scissors congruence, Campbell and Zakharevich may have shown mathematicians a new way to think about a very different part of their field: algebraic equations. 

First Cuts

Scissors congruence seems like an easy problem. More than 2,000 years ago Euclid recognized that two-dimensional shapes with the same area can be rearranged as each other. It’s reasonable to assume that higher-dimensional shapes with the same volume can be similarly recast.

But in 1900, David Hilbert suggested that the problem wasn’t so simple.

That year, in a speech at the International Congress of Mathematicians in Paris, he identified 23 open problems that he thought should guide mathematical inquiry for the next century. The third one had to do with scissors congruence. Hilbert conjectured that not all three-dimensional shapes with the same volume are scissors congruent — and he challenged mathematicians to find a pair of shapes that proved his point.

Within a year of the speech, Hilbert’s student Max Dehn did so. The timing struck many mathematicians as suspicious. “Some speculate Hilbert only included this problem because his student had already solved it,” Zakharevich said.

Whether the problem was a setup or not, Dehn’s result upended how mathematicians understood scissors congruence. He proved that a tetrahedron with a volume of 1 unit is not scissors congruent to a cube of the same volume. No matter how you cut up the former, you’ll never be able to reassemble it as the latter.

In addition to showing that volume isn’t sufficient to determine when two shapes are scissors congruent, Dehn introduced a new way of measuring shapes. He proved that any three-dimensional shapes that are scissors congruent to each other must have the same volume and also agree on this new measurement.

Dehn focused on the interior angles formed where two faces of a three-dimensional shape meet. On the inside of a cube, for instance, all faces meet at 90-degree angles. But in more complicated shapes, not all angles are equally important. Angles formed along longer edges do more to shape a shape than angles formed along shorter edges, so Dehn assigned weights to angles based on the lengths of the edges along which they’re formed. He combined this information into a complicated formula that produced a single number at the end — the “Dehn invariant” of the shape.

Dehn proved that any three-dimensional shapes that are scissors congruent must have the same volume and the same Dehn invariant. But he couldn’t answer the stronger corollary to that statement: If three-dimensional shapes have the same volume and Dehn invariant, are they necessarily scissors congruent? Jean-Pierre Sydler finally proved that they are in 1965. Three years later Børge Jessen showed that those two characteristics also determine scissors congruence in four dimensions.

Sydler’s and Jessen’s results were major advances, but mathematicians are greedy: Are volume and the Dehn invariant enough to determine scissors congruence for shapes of any dimension? And are those same measurements sufficient in geometric contexts besides normal, flat Euclidean space — settings like spherical geometry (think about latitude and longitude lines on the surface of the Earth), or the saddle-shaped universe of hyperbolic geometry?

At the end of the 20th century, a mathematician named Alexander Goncharov devised an approach that he thought could solve the whole problem once and for all — while also connecting scissors congruence with an entirely separate area of mathematics.

Strange Correspondence

Mathematics is full of unexpected connections. Zakharevich says doing mathematics is like stumbling across something odd in nature and attempting to decipher why it is the way it is.

“If you see a ring of mushrooms growing in the forest, and you don’t know how mushrooms grow, you’re going to wonder how they know to grow in a circle,” she said. “The reason is because mushrooms are really a fungus growing below ground.”

In 1996, Goncharov issued a series of conjectures that suggested the existence of a similarly hidden underground structure in mathematics. The structure, if it was there, would explain why several mathematical phenomena — including scissors congruence — work the way they do.

One of the conjectures said that a shape’s volume and its Dehn invariant are indeed enough to determine scissors congruence for shapes of any dimension and in any geometric setting.

“Goncharov said the same principles that apply in three dimensions apply in all dimensions,” said Charles Weibel of Rutgers University.

But Goncharov, now of Yale University, also predicted that this underlying structure would explain a lot more than that. He said that scissors congruence is a more universal concept — and that it applies not just to cutting up shapes, but also to cutting up shapes formed by the solutions to algebraic equations, like the graph of x² + y² + z² = 1. And the information you need to sort shapes by scissors congruence mirrors the information you need to organize algebraic equations into classes — where all equations in a class are made up of the same fundamental pieces.

It was a shocking connection, as if the same principle you used to create a taxonomy of animals somehow allowed you to sort chemical elements as well. Many mathematicians find the idea as bizarre as it sounds.

“It’s utterly mysterious. On their face these things should not be related in any way,” Campbell said.

Cutting Equations

To see how sorting geometric shapes and algebraic equations could be analogous, it helps to first understand what it means to break an equation’s solutions into parts. And to do that, let’s return to our previous example and picture the graph of solutions to x² + y² + z² = 1.

That graph is the surface of a sphere. But this surface is not just the solution to that equation: It’s also a collection of many smaller graphs, or subgraphs, of solutions to other equations. For example, you can draw a circle on the surface of the sphere, like Earth’s equator. That’s one subgraph, which represents solutions to an algebraic equation like x² + y² = 1.  Or you can isolate a single point at the north pole of the sphere, corresponding to the equation z = 1. By looking at the kinds of subgraphs you can draw within a larger graph — the kinds of building blocks it’s made of — you can learn something about the properties of the larger graph.

For more than 50 years, mathematicians have been developing a theory of the subgraphs of algebraic equations. Just as ordinary matter is made up of atoms, mathematicians think that algebraic equations are made up of fundamental pieces called “motives.” The term comes from the French word “motif,” which refers to the basic elements of a melody.

“Motives are these fundamental building blocks. They tell you everything that the [algebraic equation] is built out of, just like a melody is built out of different pieces,” Zakharevich said. The sphere, for example, is made up of circles, points and planes. Each of those is made up of constituent pieces (which emerge when you perform calculus on them), and so on all the way down, until you hit motives, the conjectured bedrock of algebraic equations.

Mathematicians would like to classify algebraic equations according to their motives in order to gain a complete, systematic perspective on the equations, which are among the most important objects in mathematics. The task is hard and remains unfinished. But in his 1996 paper, Goncharov suggested that sorting shapes according to scissors congruence and sorting algebraic equations by motive were two faces of the same problem — meaning classifying one would lead you to a principle you could use to classify the other.

The connection, he proposed, involved an analogue for the Dehn invariant. Only, instead of arising from a basic geometric calculation, this analogue should come from a similar calculation on the motives of algebraic equations (called the “motivic coproduct”).

“The idea is that this Dehn invariant problem is parallel to this other problem which involves motives,” Weibel said.

For the connection to work, though, mathematicians would need to establish that the Dehn invariant really does sort shapes into groups that are scissors congruent. Dehn himself showed that any three-dimensional shapes that are scissors congruent have the same volume and Dehn invariant. But Dehn — and everyone after him — left open the possibility that there are some higher-dimensional shapes with the same volume and Dehn invariants that nevertheless are not scissors congruent.  In their new work, Campbell and Zakharevich tried to close the door on that possibility for good.

Two for One

In June 2018, Campbell and Zakharevich spent three weeks working together at the Institute for Advanced Study in Princeton, New Jersey. Scissors congruence had intrigued them both for a long time, but Zakharevich thought Goncharov’s conjectures were too hard to tackle in such a short time frame. Campbell still wanted to give it a try, though, and Zakharevich didn’t need much convincing.

“Jonathan said, ‘We have three weeks, let’s try and reevaluate at the end of the first week.’ One week in we decided we should spend another week on this,” Zakharevich said. Two weeks in, they’d figured out many of the key ideas that anchor their new paper.

In it, they run a counterintuitive thought experiment. To get a sense of it, imagine you have a hotel with many rooms. You want to put all shapes that are scissors congruent with each other in the same room. In reality, we don’t know exactly how to identify scissors-congruent shapes — that’s the crux of the problem. But for the purposes of the thought experiment, let’s imagine that it’s possible. Or, as Zakharevich puts it, “We pretend there’s an omniscient figure that knows whether two things are scissors congruent or not.”

Once you’ve sorted shapes into their rooms, you’re going to check that all shapes in the same room have the same volume and the same Dehn invariant. Just as importantly, you’re going to check that every shape with the same volume and Dehn invariant ended up in the right room — making sure that no straggler shapes are hanging out at the hotel bar. The goal of the thought experiment is to prove that there’s a perfect one-to-one correspondence between groups of shapes that are scissors congruent and groups of shapes that have the same volume and Dehn invariant. If such a correspondence exists, it will prove that the volume and Dehn invariant truly are all you need to identify shapes that are scissors congruent.

Goncharov predicted that this perfect correspondence does indeed exist, and Campbell and Zakharevich actually proved it — conditionally. The correspondence holds true provided an additional unproven result having to do with a problem called Beilinson’s conjectures is also true.

Goncharov’s two conjectures — the one classifying scissors-congruent shapes by their volume and Dehn invariant, and the related one about classifying algebraic equations by an analogue of the Dehn invariant — are not completely settled by Campbell and Zakharevich’s proof. But it does provide mathematicians with a clearer view of how to prove them all: If you can manage to solve Beilinson’s conjectures, then thanks to Campbell and Zakharevich’s work, you get scissors congruence for free.

“Their work certainly reimagines the problem,” Weibel said. “When you tie two conjectures together like this, it illuminates the structure of the subject in a good way.”

Campbell and Zakharevich are now working with a third mathematician, Daniil Rudenko of the University of Chicago, to try and specify the connection between cutting shapes and decomposing equations that Goncharov conjectured. Rudenko previously made some modest headway on the conjectures. Now, with Campbell and Zakharevich’s work, he hopes to press ahead.

“I think this means there is a big chance that more significant progress will be made. Maybe even a proof of Goncharov’s conjectures can be obtained using this road,” Rudenko said.