New Proofs Probe Soap-Film Singularities

The gyroid is an area-minimizing surface that has been used in materials design and drug delivery.
Paul Nylander
Introduction
In the mid-19th century, the Belgian physicist Joseph Plateau — who had been designing and conducting scientific experiments since he was a child — submerged loops of wire in a soapy solution and studied the films that formed. When he bent his wire into a circular ring, a soap film stretched across it, creating a flat disk. But when he dipped two parallel wire rings into the solution, the soap stretched between them to form an hourglass shape instead — what mathematicians call a catenoid. Different wire frames produced all sorts of different films, some shaped like saddles or spiraling ramps, others so complicated they defied description.
These soap films, Plateau posited, should always take up the smallest area possible. They’re what mathematicians call area-minimizing surfaces.
It would take nearly a century for mathematicians to prove him right. In the early 1930s, Jesse Douglas and Tibor Radó independently showed that the answer to the “Plateau problem” is yes: For any closed curve (your wire frame) in three-dimensional space, you can always find a minimizing two-dimensional surface (your soap film) that has the same boundary. The proof later earned Douglas the first-ever Fields Medal.
Since then, mathematicians have expanded on the Plateau problem in hopes of learning more about minimizing surfaces. These surfaces appear throughout math and science — in proofs of important conjectures in geometry and topology, in the study of cells and black holes, and even in the design of biomolecules. “They’re very beautiful objects to study,” said Otis Chodosh of Stanford University. “Very natural, appealing and intriguing.”
Mathematicians now know that Plateau’s prediction is categorically true up through dimension seven. But in higher dimensions, there’s a caveat: The minimizing surfaces that form might not always be nice and smooth, like the disk or hourglass. Instead, they might fold, pinch or intersect themselves in places, forming what are known as singularities. When minimizing surfaces have singularities, it becomes much harder to understand and work with them.
Mathematicians consequently want to know how common such non-smooth minimizing surfaces are, and what properties they might have. If singularities are rare in a given dimension, appearing only under contrived circumstances, then they’ll disappear if you wiggle your wire frame just right. You’ll be left with a smooth minimizing surface that you can study more easily, which will give you the chance to develop a thorough understanding of such surfaces in that dimension.

Soap films stretch within wire frames to form area-minimizing surfaces.
Gift of Wesleyan University
In 1985, mathematicians proved that in eight-dimensional space, singularities can indeed be wiggled away. But in higher dimensions, “all hell breaks loose,” Chodosh said. The singularities become much more difficult to analyze. For nearly 40 years, no one could make much progress on the problem.
That barrier has finally been broken. In 2023, Chodosh — along with Christos Mantoulidis of Rice University and Felix Schulze of the University of Warwick — showed that in dimensions nine and 10, smooth minimizing surfaces are the norm. And earlier this year, the team, joined by Zhihan Wang of Cornell University, showed that the same is true in dimension 11.
The work marks a major advance toward understanding the strange kinds of minimizing surfaces that can arise in higher and higher dimensions. And mathematicians can now use the result to resolve a host of other math problems that have long been limited in scope to dimension eight or below — making those theorems even more powerful.
A Singular History
In 1962, the mathematician Wendell Fleming proved that all minimizing two-dimensional surfaces — any possible soap film that Plateau might have tried to study — must be smooth. Minimizing surfaces with singularities simply don’t exist.
These 2D surfaces exist in our familiar three-dimensional space. But what happens when we move to higher dimensions, where the problem gets harder to visualize? In four dimensions, for instance, the analogue of our wire frame is a 2D surface, and the Plateau problem asks us to find the 3D shape that fills that surface with the smallest possible volume. What might that shape look like? For all we knew, said Brian White of Stanford, “it could be very horrible — fractal-like or extremely irregular.”

Christos Mantoulidis (left), Felix Schulze (center) and Otis Chodosh showed that in dimensions nine and 10, most minimizing surfaces are smooth.
Alison Law; Courtesy of Christos Mantoulidis; Gregor Fels
In the years that followed Fleming’s proof, mathematicians showed that this never happens in four, five, six or seven dimensions. Minimizing surfaces are always smooth. But in 1968, the mathematician Jim Simons constructed a seven-dimensional shape in eight dimensions that had a singularity at just one point. The following year, mathematicians proved that this shape was a minimizing surface, establishing that minimizing surfaces in eight-dimensional space could, in fact, be singular.
The question then became: Just how bad are these singularities, really? Are they rare or common? And can you get rid of them by changing the shape of your wire frame just a bit, in just the right way? “If you want to figure out things about a surface, singularities make it much harder to analyze,” White said. But if singularities arise only rarely, and you can easily nudge them away to get a smooth surface, life becomes much easier — you can use the tools of calculus, for example.
In 1985, Robert Hardt and Leon Simon proved that minimizing surfaces in eight dimensions have this nice property, which mathematicians call generic regularity. But no one could figure out how to adapt their techniques to show whether it exists in higher dimensions.
That’s where things stood for decades — until Chodosh, Mantoulidis and Schulze stepped in.
Into Unfamiliar Domains
The three mathematicians wanted to explore uncharted higher-dimensional realms and understand the nature of their minimizing surfaces, the way a biologist might seek to understand the flora and fauna of a newly discovered island. And so they set out to see whether they could wiggle these singularities away.
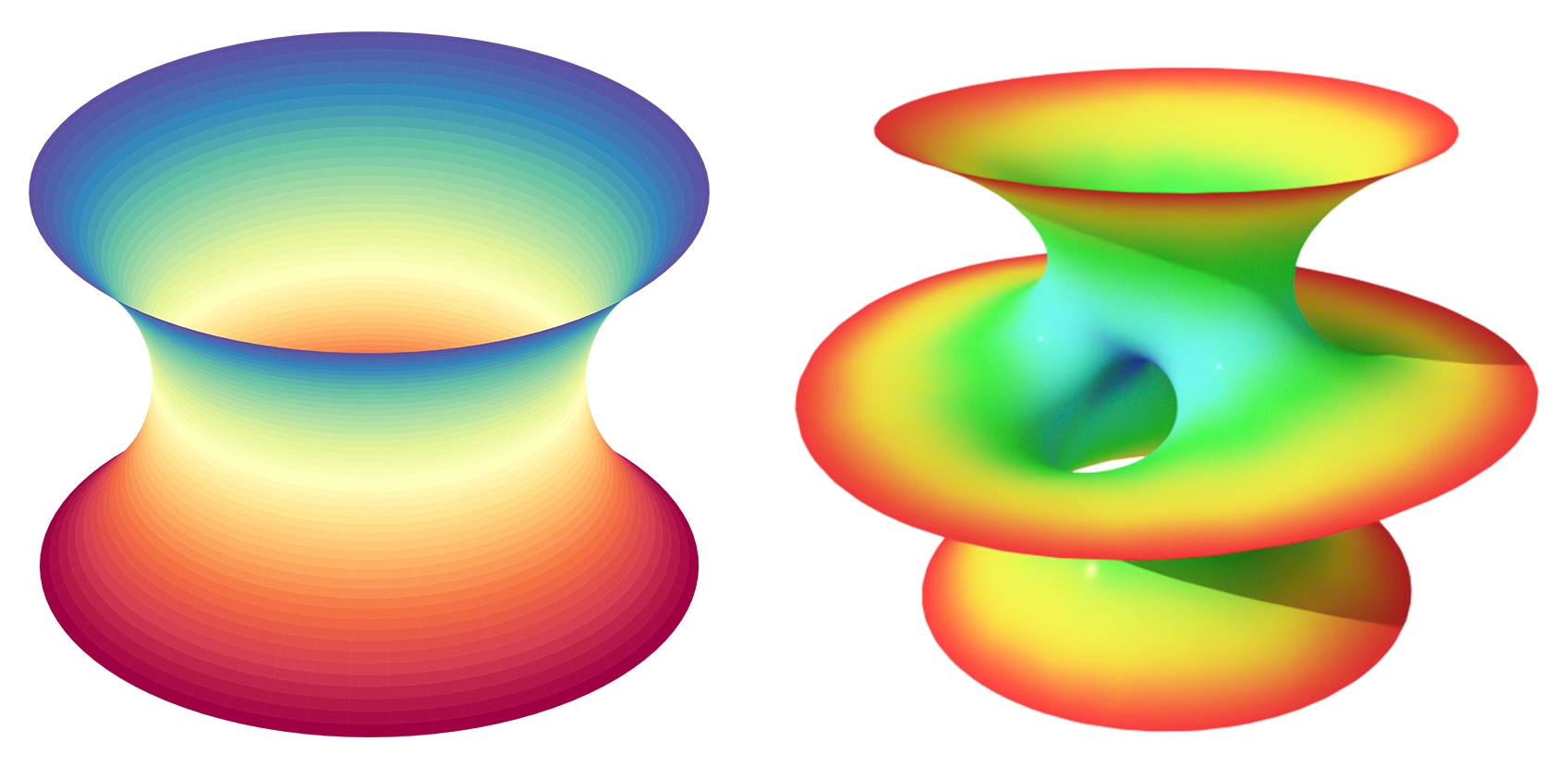
The catenoid (left) and the Costa surface are examples of area-minimizing surfaces.
Wikimedia Commons
They started by re-proving Hardt and Simon’s decades-old result in eight dimensions, this time using a different method they hoped to test out. First, they assumed the opposite of what they wanted to show: that when you slightly perturb the wire frame that defines your surface, a singularity (a single point) always persists. Each time you make a perturbation, you get a new minimizing surface that still has a singularity. You can then stack all of these minimal surfaces on top of each other, so that the points where the singularities occur form a line.
But that’s impossible. In 1970, the mathematician Herbert Federer found that any singularity on a minimizing surface in n-dimensional space can have a dimension of at most n − 8. That means that in eight dimensions, any singularity must be zero-dimensional: an isolated point. Lines aren’t allowed. Chodosh, Mantoulidis and Schulze extended Federer’s argument to apply to stacks of surfaces in eight dimensions as well. Yet in their proof, they’d produced a stack of surfaces with just such a line. The contradiction showed that their original assumption was false — meaning that you can perturb the wire frame to get rid of the singularity after all.
They now felt ready to tackle the problem in nine dimensions. They started their proof in the same way: They assumed the worst, made a series of perturbations, and ended up with an infinite stack of minimizing surfaces that all had singularities. They then introduced a new tool called a separation function, which measures the distance between these singularities. If no perturbation can interfere with the singularity, then this separation function should always stay small. But the trio was able to show that sometimes the function could get large: Some perturbations could make the singularity disappear.
The mathematicians had proved generic regularity for minimizing surfaces in dimension nine. They were able to use the same argument in dimension 10 — but in 11 dimensions, the singularities get even harder to deal with. Their techniques didn’t work for a particular kind of three-dimensional singularity. “There is a zoo of singularity types,” Mantoulidis said. “Any successful argument must be broad enough to handle all of them.”
The team decided to collaborate with Zhihan Wang, who had studied this kind of singularity extensively. Together, they honed their separation function to work in this case, too. They’d solved the problem in dimension 11.
“The fact that they extended [our understanding] by a few dimensions is really fantastic,” White said.
But they’ll likely have to find a different approach to handle higher dimensions. “We need a new ingredient,” Schulze said.
In the meantime, mathematicians expect the new result to help them make progress on other problems in math and physics. The proofs of many conjectures in geometry and topology — about the existence and behavior of shapes with certain curvature properties, for instance — rely on the smoothness of minimizing surfaces. As a result, these conjectures have only been proved up to dimension eight. Now many of them can be extended to dimensions nine, 10 and 11.
The same is true for an important statement in general relativity called the positive mass theorem, which claims, loosely speaking, that the total energy of the universe must be positive. In the 1970s, Richard Schoen and Shing-Tung Yau used minimizing surfaces to prove this statement in dimensions seven and below. In 2017, they extended their result to all dimensions. Now, the latest progress on Plateau’s problem offers a new way to confirm the positive mass theorem in dimensions nine, 10 and 11. “They provide another, more intuitive way to do the extension,” White said. “Different proofs give different insights.”
The work could also have plenty of unforeseen consequences. The Plateau problem has been used to study all sorts of other questions, including one related to how ice melts. Mathematicians hope that the team’s new methods will help deepen their understanding of these connections.
As for the Plateau problem itself, there are now two paths forward: Either mathematicians will continue to prove generic regularity in higher and higher dimensions, or they’ll discover that beyond dimension 11, it’s no longer possible to wiggle singularities away. That would be “a bit of a miracle too,” Schulze said — another mystery to unravel. “Either way, it would be very exciting.”
Editor’s Note: Jim Simons founded the Simons Foundation, which also funds this editorially independent magazine. Simons Foundation activities have no influence on our coverage.



