Latest Articles
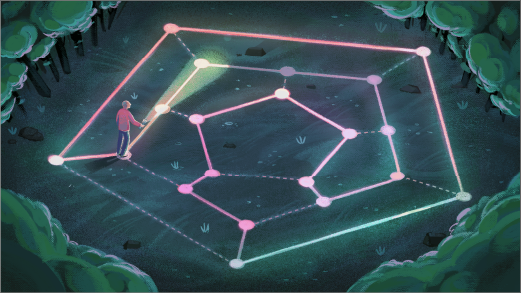
In Highly Connected Networks, There’s Always a Loop
Mathematicians show that graphs of a certain common type must contain a route that visits each point exactly once.
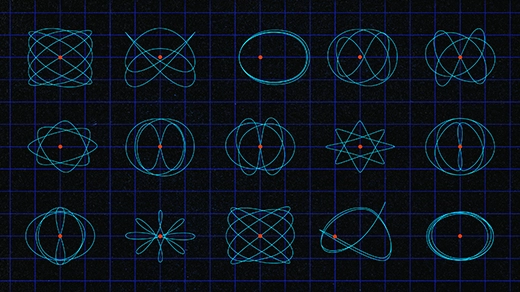
Geometers Engineer New Tools to Wrangle Spacecraft Orbits
Mathematicians think abstract tools from a field called symplectic geometry might help with planning missions to far-off moons and planets.
Number of Distances Separating Points Has a New Bound
Mathematicians have struggled to prove Falconer’s Conjecture, a simple, but far-reaching, hypothesis about the distances between points. They’re finally getting close.
Maze Proof Establishes a ‘Backbone’ for Statistical Mechanics
Four mathematicians have estimated the chances that there’s a clear path through a random maze.
The Mathematician Who Finds the Poetry in Math and the Math in Poetry
The links between math, music and art have been explored for thousands of years. Sarah Hart is now turning a mathematical eye to literature.
‘A-Team’ of Math Proves a Critical Link Between Addition and Sets
A team of four prominent mathematicians, including two Fields medalists, proved a conjecture described as a “holy grail of additive combinatorics.”
In the ‘Wild West’ of Geometry, Mathematicians Redefine the Sphere
High-dimensional spheres can have a much wider variety of structures than mathematicians thought possible.
Mathematicians Cross the Line to Get to the Point
A new paper establishes a long-conjectured bound about the size of the overlap between sets of lines and points.
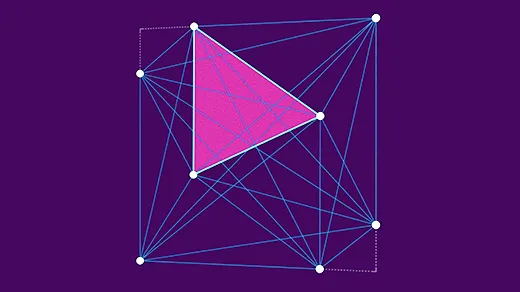
The Biggest Smallest Triangle Just Got Smaller
A new proof breaks a decades-long drought of progress on the problem of estimating the size of triangles created by cramming points into a square.