Latest Articles
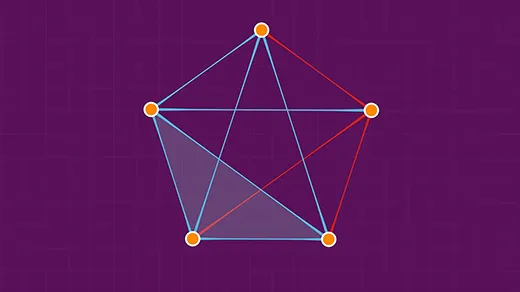
New Proof Shows That ‘Expander’ Graphs Synchronize
The proof establishes new conditions that cause connected oscillators to sway in sync.
The Lawlessness of Large Numbers
Mathematicians can often figure out what happens as quantities grow infinitely large. What about when they are just a little big?
A Very Big Small Leap Forward in Graph Theory
Four mathematicians have found a new upper limit to the “Ramsey number,” a crucial property describing unavoidable structure in graphs.
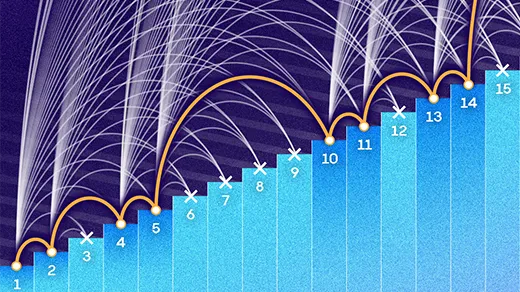
Surprise Computer Science Proof Stuns Mathematicians
For decades, mathematicians have been inching forward on a problem about which sets contain evenly spaced patterns of three numbers. Last month, two computer scientists blew past all of those results.
Coloring by Numbers Reveals Arithmetic Patterns in Fractions
In a recent paper, two mathematicians showed that a particular pattern is unavoidable when fractions are categorized.
Quantum Field Theory Pries Open Mathematical Puzzle
Mathematicians have struggled to understand the moduli space of graphs. A new paper uses tools from physics to peek inside.
Mathematicians Eliminate Long-Standing Threat to Knot Conjecture
A new proof shows that a knot some thought would contradict the famed slice-ribbon conjecture doesn’t.
Probability and Number Theory Collide — in a Moment
Mathematicians are taking ideas developed to study random numbers and applying them to a broad range of categories.
From Systems in Motion, Infinite Patterns Appear
Mathematicians are finding inevitable structures in sufficiently large sets of integers.