A Mathematician Who Dances to the Joys and Sorrows of Discovery

Jason Henry for Quanta Magazine
Introduction
“Nadie te quita lo bailado.” (No one can take from you what you’ve danced.)
For Federico Ardila, this Latin American expression epitomizes his approach to life and mathematics. It’s the driving force behind the parties he DJs in venues across the San Francisco Bay Area, where people dance till morning to the beats of his native Colombia. The dance floor is a place “where you have your freedom and you have your power, and nobody can take that away from you,” Ardila said.
He taught the expression to his students at San Francisco State University, where he is a math professor, after giving them a punishingly hard exam. San Francisco State has a highly diverse student body, and Ardila, who just turned 40, is a prominent voice in the mathematics community about how to make students from underrepresented groups — such as women and people of color — feel that they belong. But on this occasion, as he looked around at his students’ demoralized faces, he knew he had missed the mark.
“Nadie te quita lo bailado,” Ardila told his students.
“I think that’s a very powerful message — that nobody can take away from you the joy that you’ve had doing mathematics,” he told Quanta Magazine in an interview last month. “And people can give you grades, but that’s not going to take away the freedom that you felt and the fulfillment that you felt.”
The expression also applies to Ardila’s research, though not always in ways he would have chosen. Four years ago in Portland, Oregon, a thief smashed his car window and made off with a backpack containing, as luck would have it, five years’ worth of work — all of Ardila’s notes from a sweeping new paper he was developing. Proofs, examples, counterexamples and conjectures were all gone.
But the thief couldn’t steal the mathematics Ardila had “danced” in his mind. Over the past few years, Ardila and his coauthor, Marcelo Aguiar of Cornell University, have painstakingly reconstructed their work unifying the geometric and algebraic sides of combinatorics — the study of discrete structures like a social network, a sudoku puzzle or a phylogenetic tree. They finally posted their 113-page paper online in September, and in January Ardila will be presenting their work in an invited address at the Joint Mathematics Meetings, the biggest annual math conference in the United States.
Quanta spoke with Ardila at the Mathematical Sciences Research Institute in Berkeley, California, where he is visiting for the fall semester, about the mathematics he has danced and taught. The interview has been condensed and edited for clarity.
Your mathematical talent was identified quite early — in fourth grade, you got the highest score in your age group in a national math competition in Colombia.
It was actually my sister, Natalia, who first showed great promise in mathematics. I was just the little brother. She and my cousin Ana María, they both performed really, really well in this national math competition. And I think the organizers probably said, “OK, these two women are very good, and then here’s the little brother who’s coming along to the awards ceremony. Maybe he’s OK also.”
I feel like from a young age, they were paying attention to me. I never enjoyed mathematics in school very much, but my experience through the Math Olympics was much more creative and much more playful.

Federico Ardila as a child in Colombia with his mother, Amparo, and his sister, Natalia.
Jorge E. Ardila
And it turned out that it was, as many of these spaces are, a very male-dominated space, and eventually both my sister and my cousin felt uncomfortable with this space. I mean, they’re doing amazing things now; my cousin is an engineer and my sister is a music pedagogy professor. But I do think it’s kind of interesting — that was a space where I felt very comfortable and that felt very nurturing to me, and it didn’t feel so to other people. It was a space that was very “othering” for them. I think that’s always served to remind me of the role of a mathematician, of an educator, in curating the culture of a place. That’s why that’s been such a theme in my work.
You’ve said that you were surprised to get into the Massachusetts Institute of Technology, where you did your undergraduate and doctoral studies. What’s the story there?
I had never heard of MIT. And it hadn’t crossed my mind to study abroad. I was already enrolled in the local university. But my classmate told me MIT had awesome financial aid and said the math there was really good. I wanted to learn more math, so I decided to play along and apply.
At that moment I was failing most of my classes in high school. It was not clear that I was going to graduate. I had a little bit of an attitude problem. I was very interested in a lot of things but I did not like being told, “Read this” or “Think this way.” I just kind of wanted to do things on my own terms.
I was failing, I think, six out of eight subjects. Had I known what MIT was, I should have known not to apply. There is no way I should have applied with that kind of transcript.
I like telling this story to my students because I think we often close doors to ourselves by thinking that we’re not eligible or that we’re not good enough. And especially if you’re somebody who feels “othered” in your discipline or who feels like you’re lacking confidence, it’s easy to close doors on yourself. There’s a lot of people in life who are ready to close doors for you, so you can’t do it for yourself.
When you came to the United States, as an undergraduate at MIT, it was your turn to feel like the “other.”
It’s not that anybody did anything to mistreat me or to doubt me or to explicitly make me feel unwelcome, but I definitely felt very different. I mean, my mathematical education was outstanding and I had fantastic access to professors and really interesting material, but I only realized in retrospect that I was extremely isolated.
There’s a system in place that makes certain people comfortable and others uncomfortable, I think just by the nature of who’s in the space. And I say that without wanting to point fingers, because I think you can be critical about the spaces that “other” you, but you also have to be critical about the ways in which you “other” other people.
I think because mathematics sees itself as very objective, we think we can just say, “Well, logically, this seems to make sense that we’re doing everything correctly.” I think sometimes we’re a little bit oblivious as to what is the culture of a place, or who feels welcome, or what are we doing to make them feel welcome?
So when I try to create mathematical spaces, I try to be very mindful of letting people be their full human selves. And I hope that will give people more access to tools and opportunities.
What are some of the ways you do that in your teaching?
In a classroom I’m the professor, and so in some sense I’m the culture keeper. And one thing that I try to do — and it’s a little bit scary and it’s not easy — is to really try to shift the power dynamic and make sure that students feel like equally powerful contributors to the place. I try to create spaces where we’re kind of together constructing a mathematical reality.
So, for example, I taught a combinatorics class, and in every single class every single student did something active and communicated their mathematical ideas to somebody else. The structure of the class was such that they couldn’t just sit there and be passive.
I believe in the power of music, and so I got each one of them to play a song for the rest for us at the beginning of each class. At the beginning it felt like this wild experiment where I didn’t know what was going to happen, but I was really moved by their responses.
Some of them would dedicate the song to their mom and talk about how whenever they’re studying math, they’re very aware that their mom worked incredibly hard to give them the opportunity to be the first ones in their family to go to college. Another student played this song in Arabic called “Freedom.” And she was talking about how in this day and age it’s very difficult for her to feel at home and welcome and free in this country, and how mathematics for her is a place where nobody can take her freedom away.
That classroom felt like no other classroom that I’ve ever taught in. It was a very human experience, and it was one of the richest math classrooms that I’ve had. I think one worries when you do that, “Are you covering enough mathematics?” But when students are engaged so actively and when you really listen to their ideas, then magic happens that you couldn’t have done by preparing a class and just delivering it.
Mathematics has this stereotype of being an emotionless subject, but you describe it in very emotional terms — for instance, in course curricula you promise your students a “joyful” experience.
I think doing mathematics is tremendously emotional, and I think that anybody who does mathematics knows this. I just don’t think that we have the emotional awareness or vocabulary to talk about this as a community. But you walk around this building and people are making these discoveries, and there are so many emotions going on — a lot of frustration and a lot of joy.
I think one thing that happens is we don’t acknowledge this as a culture — because mathematics is emotional in sometimes very difficult ways. It can really make you feel very bad about yourself sometimes. You can be pushing on something for six months and then have it collapse, and that hurts. I don’t think we talk about that hurt enough. And the joy of discovering something after six months of working on it is really deep.
Your own research is in combinatorics. And the paper you’ll be presenting at the Joint Mathematics Meetings connects two different ways of understanding combinatorial structures, through the lenses of geometry and algebra. How do those two approaches work?
When you look at the geometric side of things, suppose, for example, you want to study the permutations (the ways of rearranging a collection of objects). It’s pretty well known that if you have n objects, the number of ways of putting them in a row is n factorial (the product n(n-1)(n-2)…1). So it’s not a very interesting problem to count how many ways there are. But what is their inherent structure?
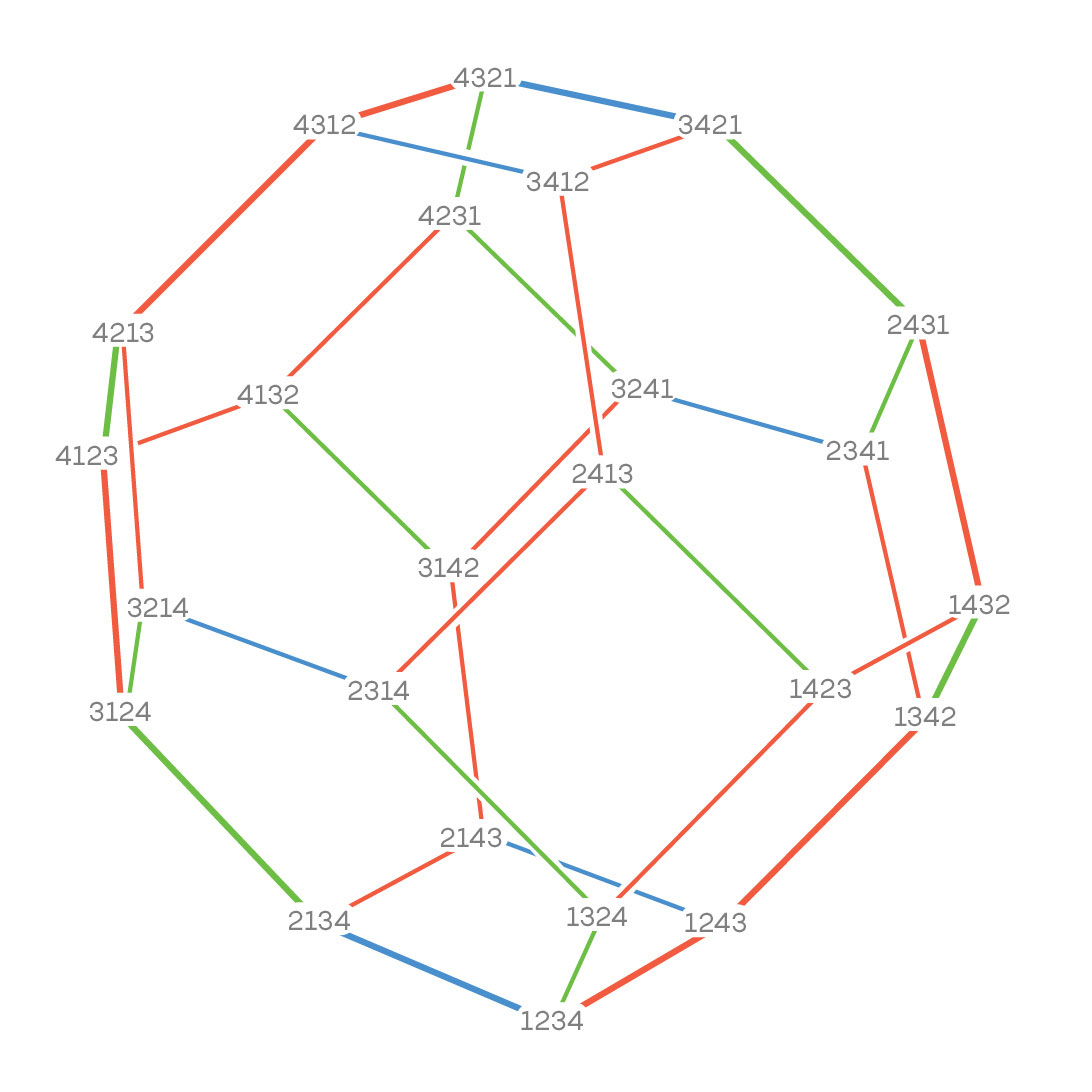
The three-dimensional permutahedron, a geometric depiction of the ways to rearrange the numbers 1, 2, 3 and 4. Two permutations are connected by an edge if one can be transformed into the other by swapping two consecutive numbers.
If you look at when two permutations are related to each other by just swapping two elements, then you start understanding not only how many there are but how are they related to each other. And then, when you say, “OK, let’s take all the permutations, and put an edge between two of them if they’re a swap away,” then you find that you get this beautiful shape that’s a polytope (a geometric object with flat sides). I think it’s completely surprising initially that the inherent relations between permutations are captured in this beautiful polytope called a permutahedron. So all of a sudden you have this geometric model, and you can use tools from polytope theory to try to say new things about permutations. And that polytope has existed for a long time and is very well understood.
And then you can also think of permutations algebraically — there’s a natural sort of “multiplication” on permutations, in which the product of two permutations is the permutation you get by doing one permutation after the other.
This is one of the most important objects in algebra, this group of permutations.
There are these two traditions, to take combinatorial objects and either make them geometric or make them algebraic. This project with Marcelo Aguiar was about trying to bring together these two points of view, and in fact we discovered that polytopes like the permutahedra have an additional related algebraic structure. I think we found a really beautiful connection between the geometric and the algebraic structure of combinatorial objects. We got a dozen results just from building this architecture and then reaping the benefits.
For many, though by no means all, mathematicians, teaching takes a back seat to research. But for you, it seems that teaching and research are very much intertwined. You often give your students open-ended problems, and you’ve co-authored many papers with students.
I love working with students. And I love sharing the joy of discovery with them. Most of my students are master’s and undergrad students, because San Francisco State doesn’t have a Ph.D. program. I think that has steered my research to things that are more immediately accessible. But still, I need the questions to be very deep.
I’m very excited about my research. I think I’m doing the most interesting research of my life right now. People tell you at 40 you start declining, and I feel like I’m getting good now.

Federico Ardila DJing at the 2017 Life Is Living Festival in Oakland.
Jason Henry for Quanta Magazine
Almost a decade ago you founded a DJ collective based in Oakland. How does that tie into your work as a mathematician and teacher?
When I DJ I’m really looking for joy, and I’m looking to create an atmosphere where people can build bridges and connect. My professor side comes out a little bit, because I play a lot of stuff that people don’t know, and I try to play music from many places that they haven’t thought about.
I also see music as a tool for social change. Some of the events I do are social benefits — it’s about music, but it’s also about feeding the soul and getting ready for the change that you want to make in the world. It feels very similar to the kind of atmosphere that I try to create in a classroom. I see all of these things as being connected.
This article was reprinted on Wired.com.