Rainbow Proof Shows Graphs Have Uniform Parts

On January 8, three mathematicians posted a proof of a nearly 60-year-old problem in combinatorics called Ringel’s conjecture. Roughly speaking, it predicts that graphs — Tinkertoy-like constructions of dots and lines — can be perfectly built out of identical smaller parts.

Mathematicians are excited that the new proof finds it’s true.

“A big reason for happiness is that this solves a very old conjecture that people couldn’t solve with other methods,” said Gil Kalai, a mathematician at the Hebrew University of Jerusalem and IDC Herzliya who was not involved in the work.

Ringel’s conjecture predicts that certain kinds of complicated graphs — think Tinkertoy designs with trillions of pieces or more — can be “tiled,” or covered completely, by any individual copy of certain smaller graphs. Conceptually, the statement is like looking at a kitchen and asking: Can I completely cover the floor with identical copies of any type of tile in the store? In real life, most tiles won’t work for your particular kitchen — you’ll have to combine different shapes to cover the whole floor. But in the world of graph theory, the conjecture predicts that the tiling always works.

With the kitchen floor, as with graphs, where you place the first tile matters. The new work addresses this critical question about placement in a way that’s both surprising and surprisingly intuitive.

The Forest and the Trees

In combinatorics, mathematicians study the way vertices (dots) and edges (lines) combine to form more complicated objects called graphs. You can ask many different questions about these graphs. One of the most basic is this: When do smaller, simpler graphs fit perfectly inside larger, more complicated ones?

“You have puzzle pieces and you’re not sure if the puzzle can be put together from the pieces,” said Jacob Fox of Stanford University.

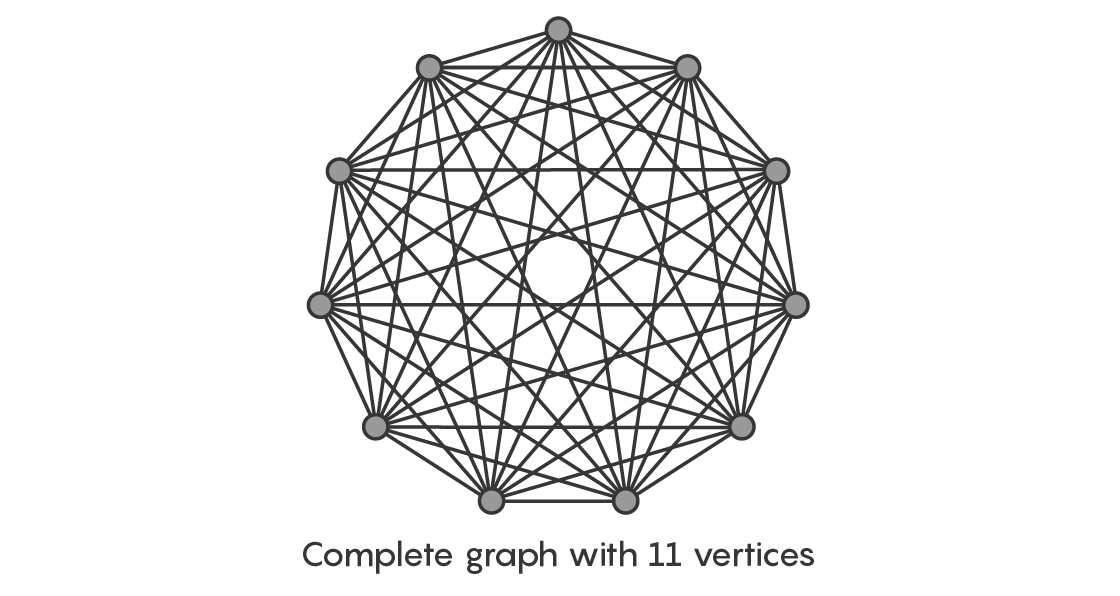
In 1963, a German mathematician named Gerhard Ringel posed a simple but broad question of that sort. First, he said, start with any odd number of vertices greater than 3 (the number needs to be odd for the conjecture to be plausible, as we’ll see in a moment). Draw edges between them so that every vertex is connected to every other vertex. This creates an object called a complete graph.

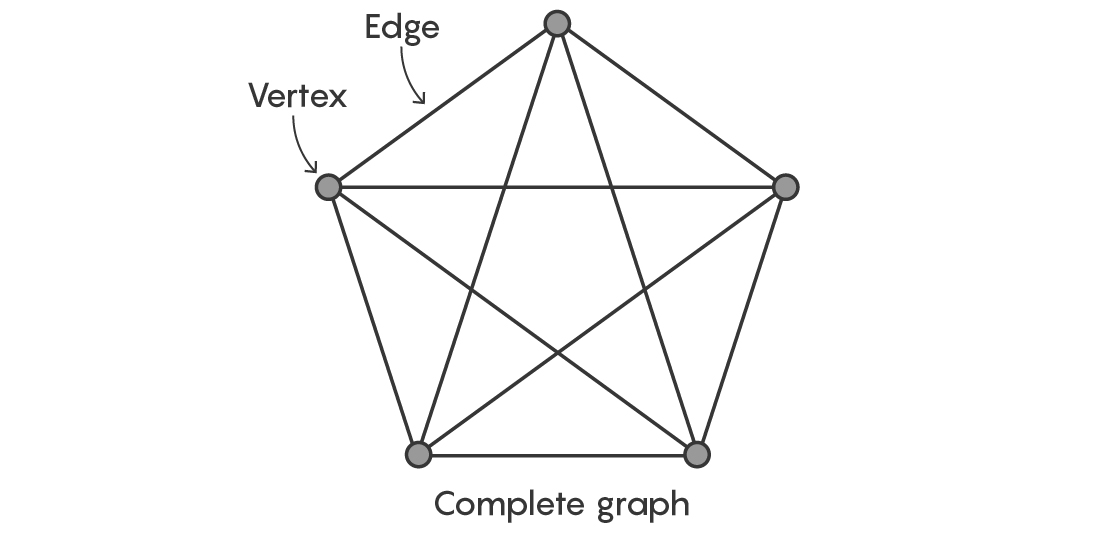
Next, think about a different type of graph. It could be a simple path — edges connected in a line. Or it could be a path with other edges branching off of it. You could add branches to the branches. You could make the graph as complicated as you want, so long as it doesn’t contain any closed loops. These types of graphs are called trees.

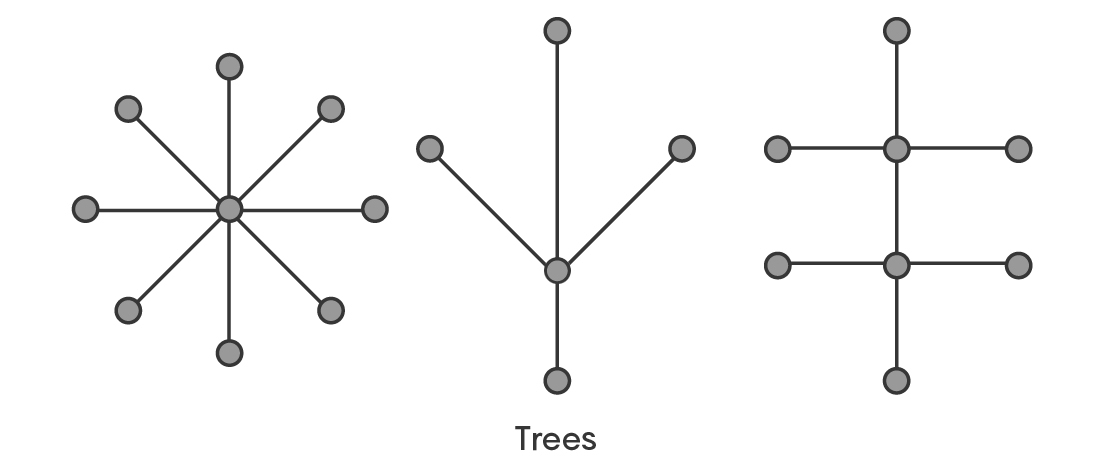
Ringel’s question was about the relationship between complete graphs and trees. He said: First imagine a complete graph containing 2n + 1 vertices (that is, an odd number). Then think about every possible tree you can make using n + 1 vertices — which is potentially a lot of different trees.

Now, pick one of those trees and place it so that every edge of the tree aligns with an edge in the complete graph. Then place another copy of the same tree over a different part of the complete graph.

Ringel predicted that if you keep going, assuming you started in the right place, you’ll be able to tile the complete graph perfectly. This means that every edge in the complete graph is covered by an edge in a tree, and no copies of the tree overlap each other.

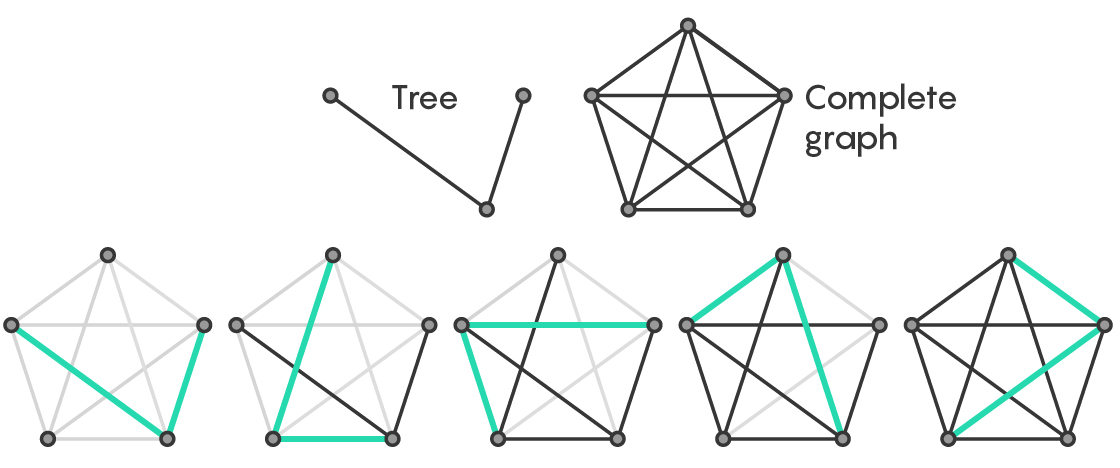
“I can take copies of the tree. I put one copy on top of the complete graph. It covers some edges. I keep doing this and the conjecture says you can tile everything,” said Benny Sudakov of the Swiss Federal Institute of Technology Zurich, a co-author of the new proof with Richard Montgomery of the University of Birmingham and Alexey Pokrovskiy of Birkbeck College, University of London.

Finally, Ringel predicted that the tiling works regardless of which of the many different possible trees you use to perform it. This might seem wildly broad. Ringel’s conjecture applies equally to complete graphs with 11 vertices and complete graphs with 11 trillion and 1 vertices. And as the complete graphs get bigger, the number of possible trees you can draw using n + 1 vertices also skyrockets. How could each and every one of those trees perfectly tile the corresponding complete graph?

But there were reasons to think Ringel’s conjecture might be true. The most immediate one was that simple combinatoric arithmetic didn’t rule the conjecture out: The number of edges in a complete graph with 2n + 1 vertices can always be evenly divided by the number of edges in a tree with n + 1 vertices.

“It’s an important thing that the number of edges in the tree divides the number of edges in the complete graph,” said Montgomery.

Mathematicians quickly identified another piece of evidence that suggested the conjecture was at least feasible, and it set in motion a chain of discovery that eventually led to a proof.

Place and Rotate

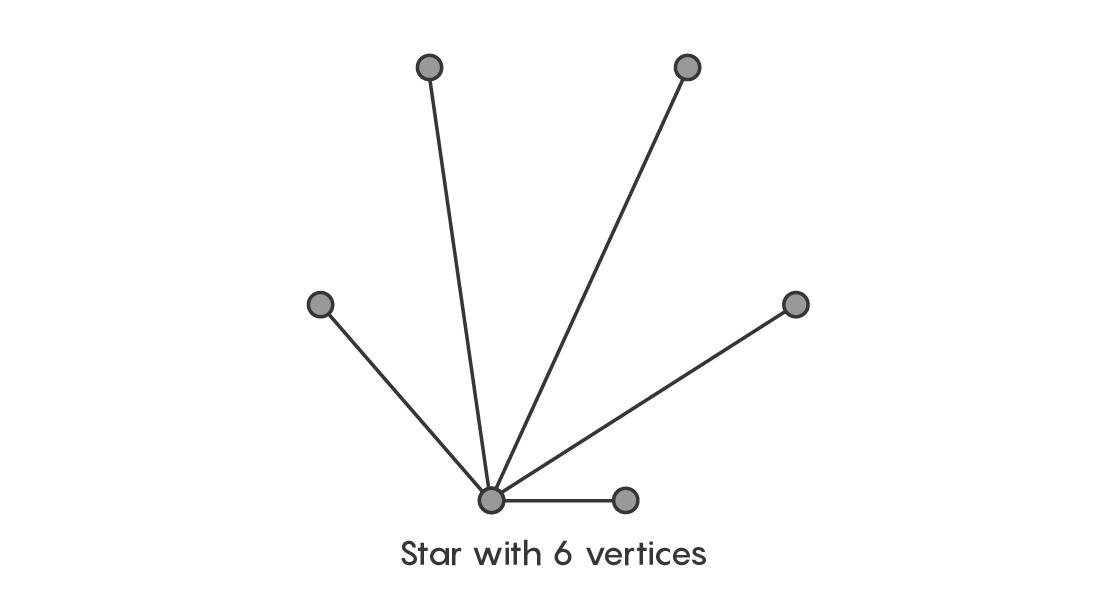
One of the simplest trees of all is a star: a central vertex with edges radiating out from it. But it’s different from the typical image of a star, since the edges don’t have to be arrayed uniformly around the vertex. They just have to extend out from the same place, and they can’t intersect each other anywhere but at the central vertex. If you wanted to probe Ringel’s conjecture, the tree that looks like a star would be a natural place to start.

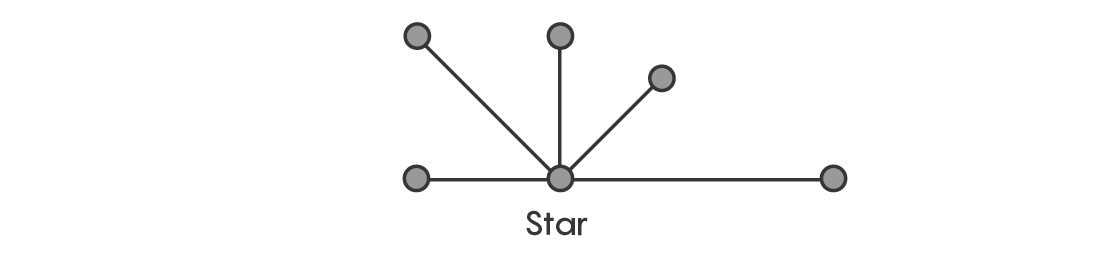
And indeed, mathematicians quickly observed that the star with n + 1 vertices can always perfectly tile a complete graph with 2n + 1 vertices. That fact alone is interesting, but the way to prove it really got mathematicians thinking.

Consider a simple example. Start with 11 vertices. Arrange these vertices in a circle and then connect each vertex with every other vertex to form a complete graph.

Now consider the corresponding star: a central point with five edges extending out from it.

Next, place the star so that the central vertex aligns with one of the vertices in the complete graph. You’ll cover some but not all of the edges. Now reposition the star one vertex to the left, as if you were turning the face of a compass. You’ll have a new copy of your star that overlaps an entirely distinct set of edges on the complete graph.

Keep rotating the star, one unit at a time. By the time you get back to where you started, you’ll have tiled the entire complete graph without any of your stars overlapping, just as Ringel predicted.

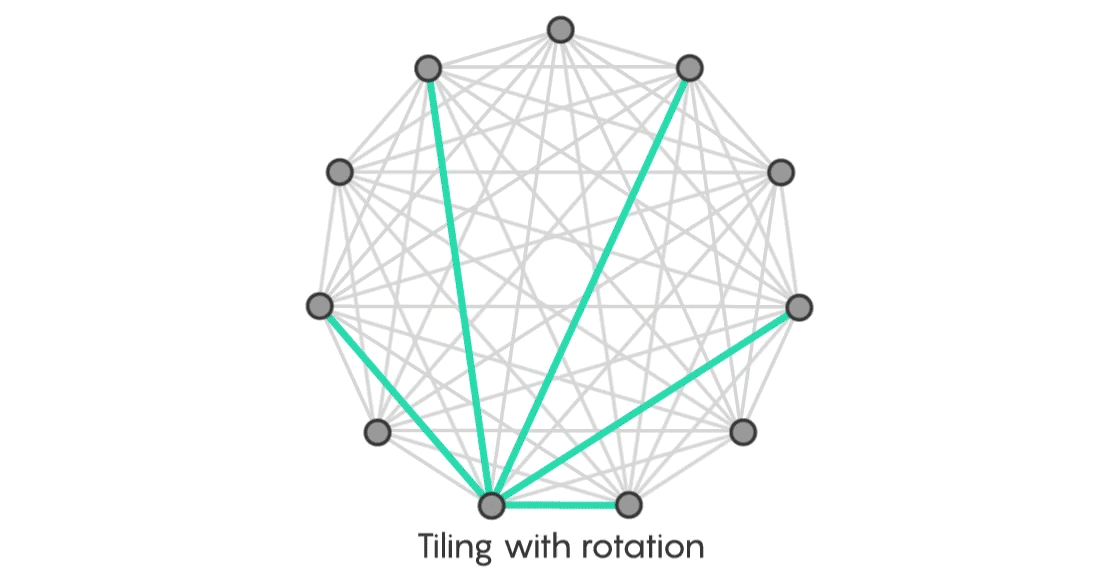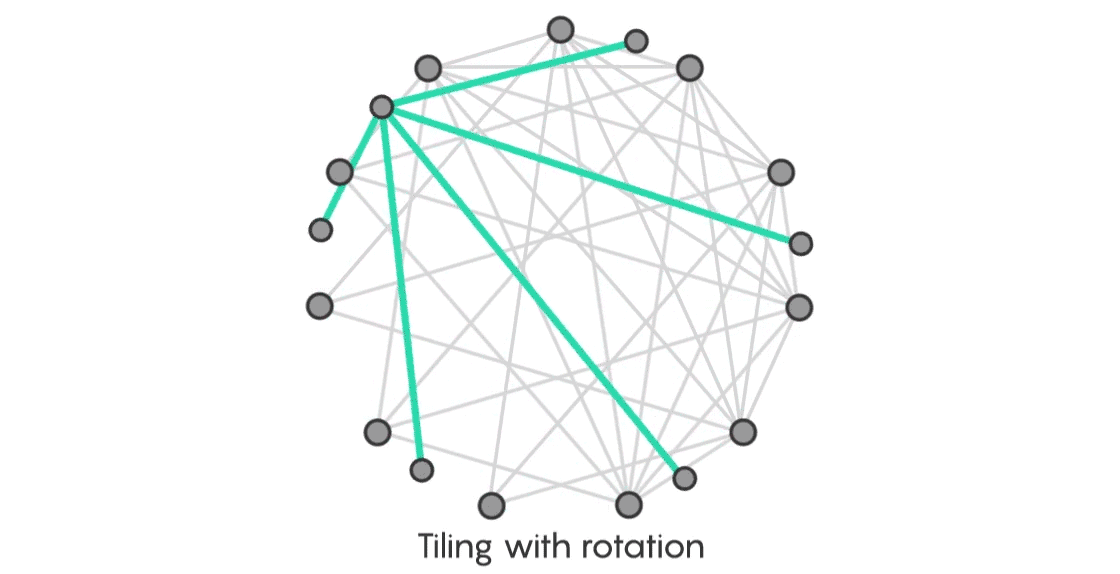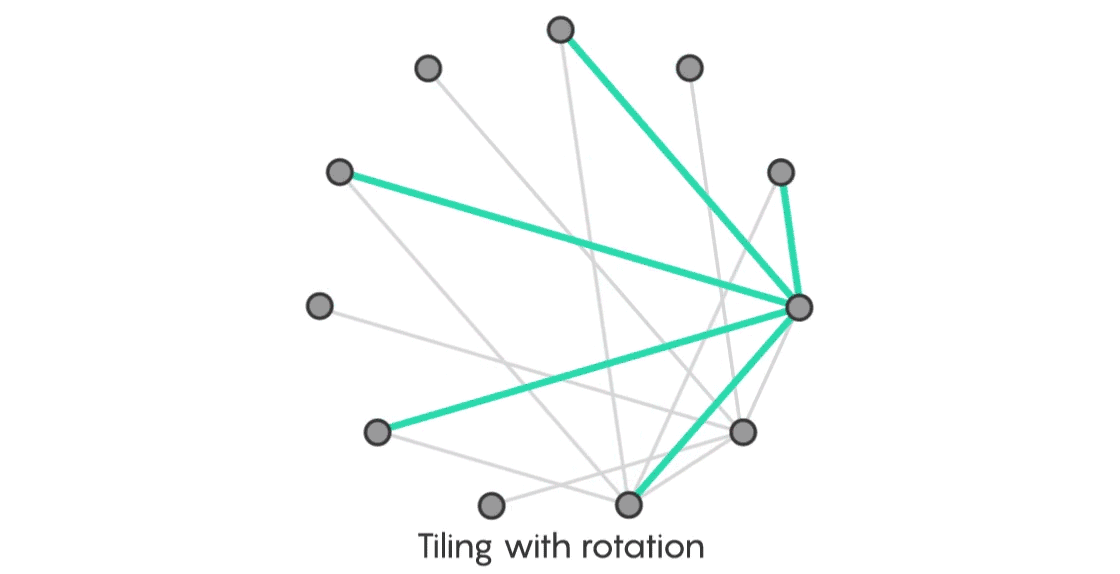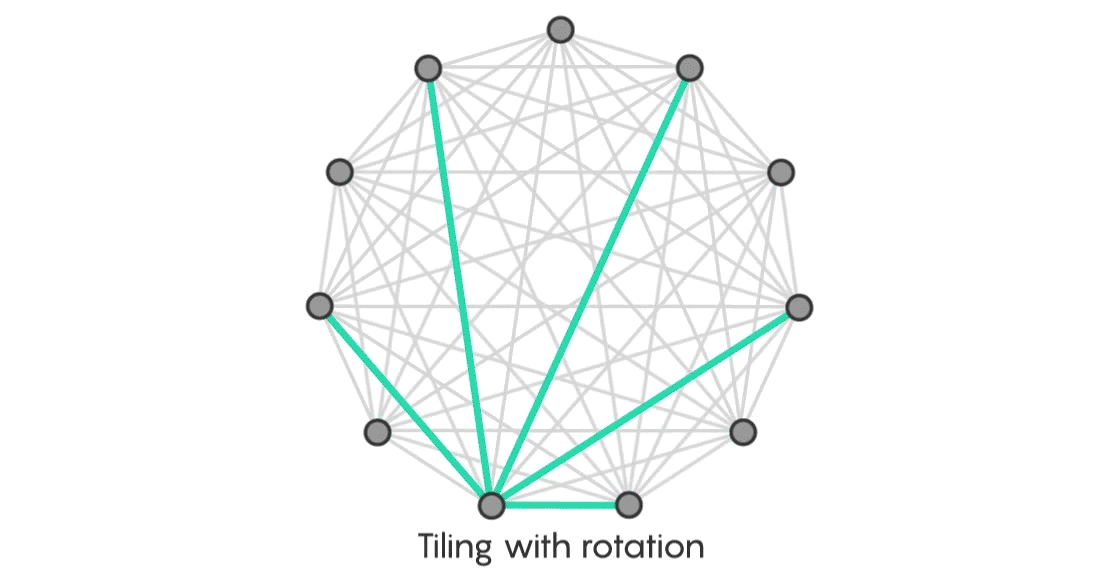
“We know the conjecture is not completely bogus if the tree is a star,” Sudakov said. “Moreover, we can show it in this beautiful way: Put the graph on a circle, shift the star, get new copies, and that’s how tiling will go.”

Shortly after Ringel released his conjecture, a Slovak-Canadian mathematician named Anton Kotzig used this example to make a prediction that was even bolder than Ringel’s. While Ringel said that every complete graph with 2n + 1 vertices can be tiled by any tree with n + 1 vertices, Kotzig conjectured that the tiling can always be done exactly the way it’s done with the star: by placing the tree on the complete graph and then simply rotating it.

It seemed like a fanciful idea. The star is symmetric, and as a result it doesn’t matter how you place it. Most trees, though, are gnarly. They have to be placed exactly right for the rotational method to work.

“The star has this simple structure that lets you place it by hand, but if you have a wild tree with lots of different branches of different lengths, it’s hard to imagine how to find a careful placement of that,” Pokrovskiy said.

If mathematicians were going to solve Ringel’s conjecture using Kotzig’s rotational method, they would have to figure out how to place the first copy of the tree to avoid the thicket. Luckily, they ended up finding a colorful solution.

Rainbow Colorings

Color-coding often makes life easier. It can help you organize your calendar or quickly distinguish among lunchboxes in a big family. Turns out, it’s also an effective way to figure out how to place that first tree inside a complete graph.

Think again about the complete graph with 11 vertices arrayed around a circle. You’re going to color-code its edges according to a simple rule, one that concerns the distance between two vertices connected by an edge.

That distance is defined as the number of spaces around the circle you need to go to move from one vertex to another. (No shortcuts through the inside of the circle.) Of course, you can always go one of two ways around a circle, so consider the distance to be the shorter route between two vertices. If the vertices are adjacent to each other, the distance between them is 1, not 10. If two vertices are separated by one other vertex, the distance between them is 2.

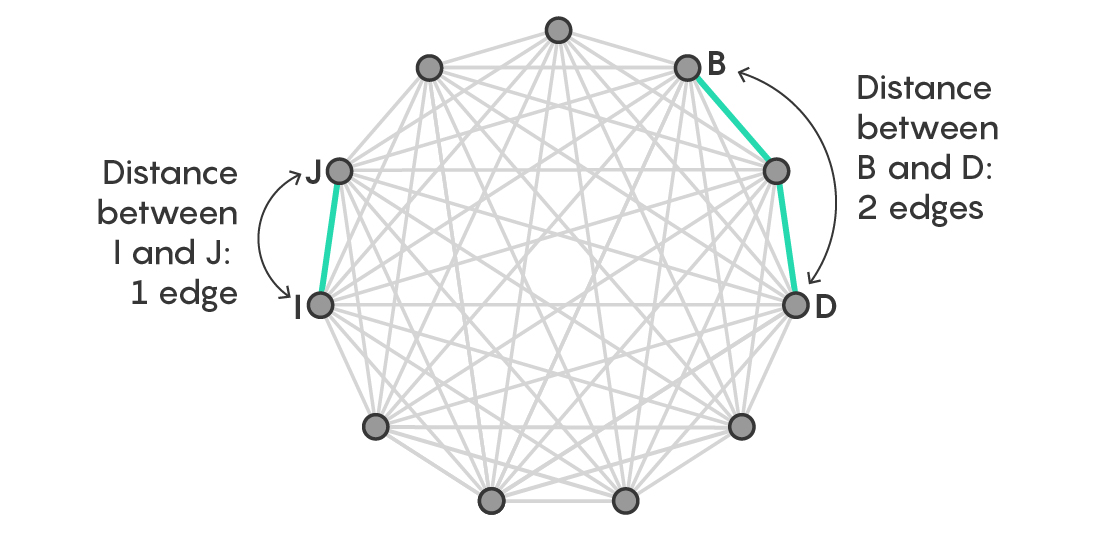
Now color the edges of the graph according to distance. All edges connecting vertices that are one unit apart receive the same color, say, blue. All edges connecting vertices that are two units apart receive the same color, say, yellow.

Keep going like this, so that edges connecting vertices the same distance apart all receive the same color. You’ll also want to use a different color for each distance. On a complete graph with 2n + 1 vertices, you’ll need n different colors to carry out the scheme. At the end you’ll have a pretty design — and a useful one, too.

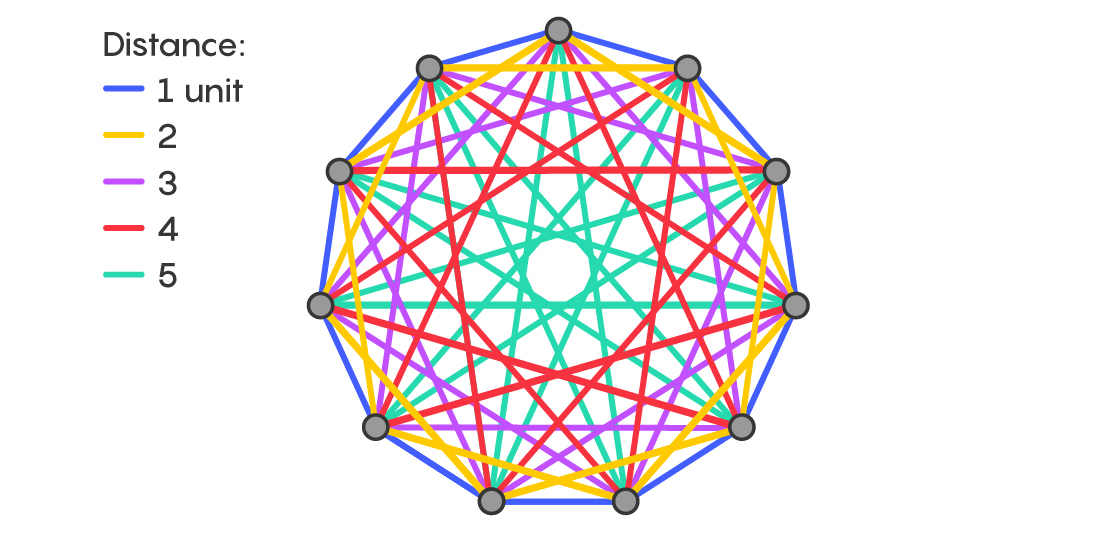
Soon after Ringel and Kotzig proposed their conjectures, Kotzig realized that this coloring of the complete graph could serve as a guide for how to place a tree over it.

The idea was to position the tree so that it covers one edge of each color and doesn’t cover any color twice. Mathematicians call this placement a rainbow copy of the tree. Since the coloring requires n colors, and the tree with n + 1 vertices has n edges, right away we know it’s at least possible that there could always be a rainbow copy.

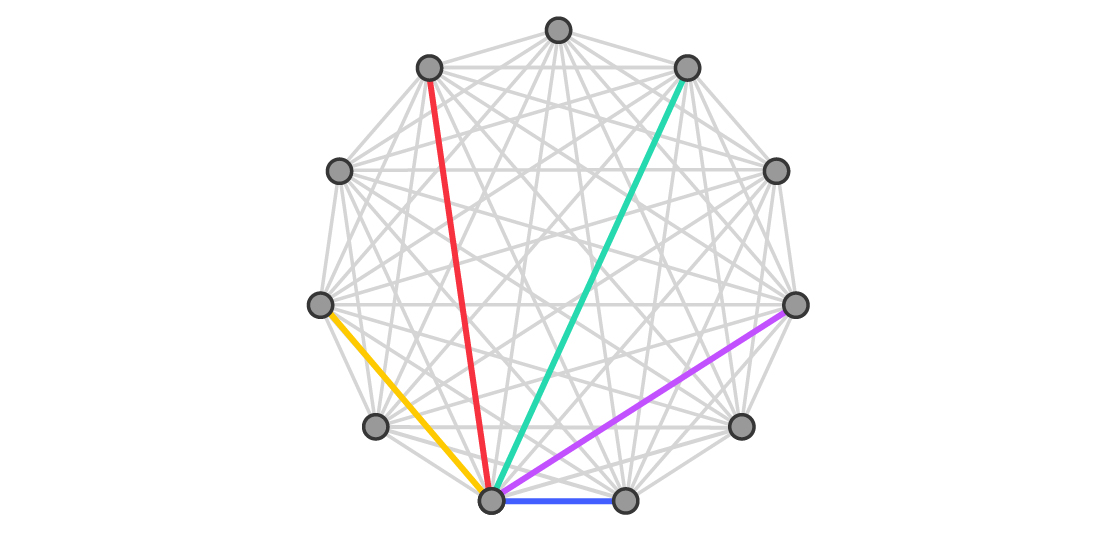
By the late 1960s, mathematicians understood that the rainbow copy of the tree has a very special property: It’s the exact right starting position from which to rotate the tree in order to tile the graph.

“If you get a rainbow copy, the tiling always works out,” Pokrovskiy said.

Now mathematicians knew they could prove Ringel’s conjecture by proving that every complete graph with 2n + 1 vertices contains a rainbow copy of every tree with n + 1 vertices. If the rainbow copy always exists, the tiling always works.

But proving that something always exists is hard. In order to do it, mathematicians would have to establish that complete graphs can’t help but contain rainbow copies of trees. It took more than 40 years, but that’s just what Sudakov and his co-authors did in their new proof.

Perfect Packing

Imagine you’re handed a complete graph with 11 vertices, and a tree with six. The complete graph has been colored with five different colors. The tree has five edges. Your task is to find a rainbow copy of the tree inside the complete graph.

You could simply place the edges of the tree on the graph one at a time. The first edge is easy to place: It can go on any edge of any color. The second edge is only slightly harder. It can go almost anywhere, just not on an edge of the complete graph that’s the same color as the one you’ve already covered. But as you keep placing edges of your tree, the job of placing the next one keeps getting harder. By the time you get to the last edge of the tree, you no longer have any choice about which color it will cover — there’s only one left. You’d better hope you did a good job planning ahead.

This idea, that the task of finding a rainbow copy of a tree gets harder as you place more edges of the tree, was central to the way the three mathematicians approached their proof. They looked for ways to give themselves as much flexibility as possible at the end of the process.

They knew from the outset that it’s easy to find rainbow copies of very simple trees — trees in the shape of a long path, or a long path with a few short branches. The hardest trees to place correctly were ones with many edges converging at a single vertex, like stars, but with a more unwieldy and irregular shape. Placing those is like trying to pack a stroller in the trunk of a car when it’s already half full.

“The difficulty comes in when you’re trying to pack the complete graph with inflexible things that look like stars,” Pokrovskiy said.

As anyone who’s ever packed a trunk knows, you should always begin with the most difficult objects: the largest suitcases and big, inflexible objects like bicycles. You can always stuff jackets in at the end. The mathematicians adopted this philosophy, too.

Imagine a tree with 11 edges. Six come together at a central vertex. Most of the rest form a single shape coming off it, like a tendril.

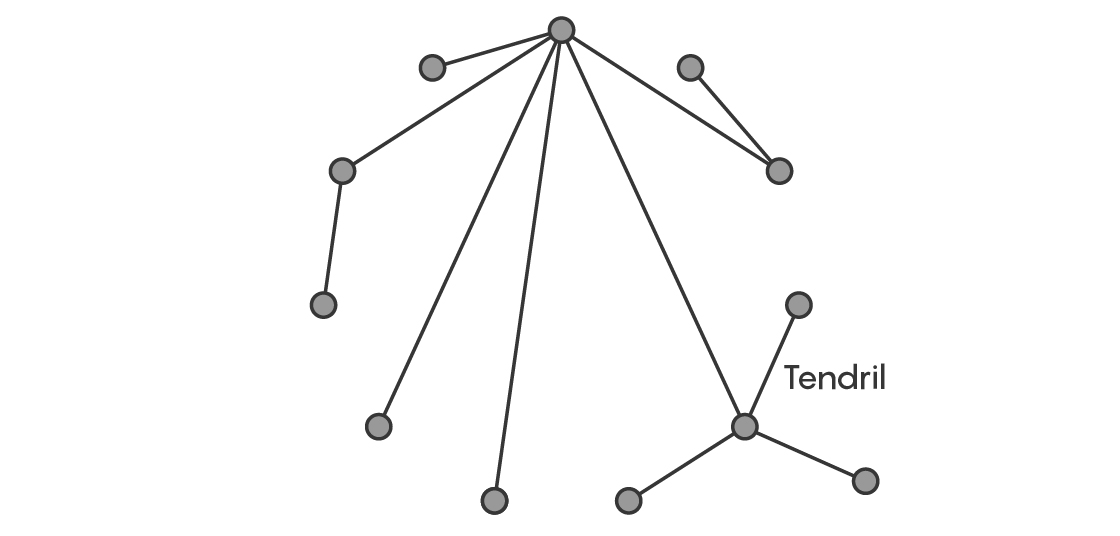
The hardest part of the tree to place is the vertex with six edges. So the mathematicians separated it from the rest of the tree and placed it first, with the intention of eventually reattaching the other part, just as you might disassemble a bed to move it upstairs, and then put it back together once you had it in your room. In fact, they didn’t just place the star portion once — they found different places to put copies of the star inside the complete graph.

Then they randomly chose one. By doing this, they ensured that the remaining space in the complete graph was also random — meaning it had a roughly equal distribution of edges of different colors. This was the space in which they’d need to place the rest of the tree — the path portion they’d set aside.

They faced some constraints in the way they could place it. The path would have to connect with the star part they’d already placed, and it would also have to cover colors that had not already been covered by the star it was connected to.

But the mathematicians had given themselves options. They could connect the path to almost any one of the different copies of the star. Even better, because the space around the star was random as well, the mathematicians had options about which colors they covered with the remaining part of the tree.

“At the end of the embedding, when things are getting difficult, instead of having one color I must use, I have a little choice,” Montgomery said.

The three mathematicians finished their proof with a probabilistic argument. They showed that once they embedded the hardest parts of a tree, if the remaining space in the complete graph was essentially random, there would always be a way they could embed the remainder of the tree to get a rainbow copy.

“You can use what you left out at the beginning to kind of absorb what was left of the tree to create a total rainbow coloring,” said Noga Alon of Princeton University.

The mathematicians did not come up with an exact way to find a rainbow copy of every tree with n + 1 vertices in every complete graph with 2n + 1 vertices. But they did prove that a rainbow copy has to be present.

And if the rainbow copy always exists, then it’s always possible to perform exactly the kind of tiling that Ringel predicted. The conjecture is true.

The proof also provides new tools for solving similar unsolved problems in combinatorics, such as “graceful labeling,” which predicts that the tiling of a complete graph can be performed under more stringent conditions, where the tree has to be placed with even greater precision.

“It shows the methods people have been thinking about for a while are indeed quite powerful,” Fox said. “When you properly adapt them, you can solve these questions that had seemed out of reach.”

Correction: February 19, 2020
One of the tree examples was missing a vertex where edges branched off. The missing vertex has been added to the figure.