Mathematicians Settle Erdős Coloring Conjecture
Mathematicians have now proven that to color the edges of a linear hypergraph, you never need more colors than the number of vertices in the graph.
Introduction
In the fall of 1972, Vance Faber was a new professor at the University of Colorado. When two influential mathematicians, Paul Erdős and László Lovász, came for a visit, Faber decided to host a tea party. Erdős in particular had an international reputation as an eccentric and energetic researcher, and Faber’s colleagues were eager to meet him.
“While we were there, like at so many of these tea parties, Erdős would sit in a corner, surrounded by his fans,” said Faber. “He’d be carrying on simultaneous discussions, often in several languages about different things.”
Erdős, Faber and Lovász focused their conversation on hypergraphs, a promising new idea in graph theory at the time. After some debate they arrived at a single question, later known as the Erdős-Faber-Lovász conjecture. It concerns the minimum number of colors needed to color the edges of hypergraphs within certain constraints.
“[It] was the simplest possible thing we could come up with,” said Faber, now a mathematician at the Institute for Defense Analyses’ Center for Computing Sciences. “We worked on it a bit during the party and said, ‘Oh well, we’ll finish this up tomorrow.’ That never happened.”
The problem turned out to be much harder than expected. Erdős frequently advertised it as one of his three favorite conjectures, and he offered a reward for the solution, which increased to $500 as mathematicians realized the difficulty. The problem was well known in graph theory circles and attracted many attempts to solve it, none of which were successful.
But now, nearly 50 years later, a team of five mathematicians has finally proved the tea-party musing true. In a preprint posted in January, they place a limit on the number of colors that could ever be needed to shade the edges of certain hypergraphs so that no overlapping edges have the same color. They prove that the number of colors is never greater than the number of vertices in the hypergraph.
The approach involves carefully setting aside some edges of a graph and randomly coloring others, a combination of ideas that researchers have wielded in recent years to settle a number of long-standing open problems. It wasn’t available to Erdős, Faber and Lovász when they dreamed up the problem. But now, staring at its resolution, the two surviving mathematicians from the original trio can take pleasure in the mathematical innovations their curiosity provoked.
“It’s a beautiful work,” said Lovász, of Eötvös Loránd University. “I was really pleased to see this progress.”
Just Enough Colors
As Erdős, Faber and Lovász sipped tea and talked math, they had a new graph-like structure on their minds. Ordinary graphs are built from points, called vertices, linked by lines, called edges. Each edge joins exactly two vertices. But the hypergraphs Erdős, Faber and Lovász considered are less restrictive: Their edges can corral any number of vertices.
This more expansive notion of an edge makes hypergraphs more versatile than their hub-and-spoke cousins. Standard graphs can only express relationships between pairs of things, like two friends in a social network (where each person is represented by a vertex). But to express a relationship between more than two people — like shared membership in a group — each edge needs to encompass more than two people, which hypergraphs allow.
However, this versatility comes at a price: It’s harder to prove universal characteristics for hypergraphs than for ordinary graphs.
“Many of the miracles [of graph theory] either vanish or things become much harder when you move to hypergraphs,” said Gil Kalai of IDC Herzliya and the Hebrew University of Jerusalem.
For instance, edge-coloring problems become harder with hypergraphs. In these scenarios, the goal is to color all the edges of a graph (or hypergraph) so that no two edges that meet at a vertex have the same color. The minimum number of colors needed to do this is known as the chromatic index of the graph.
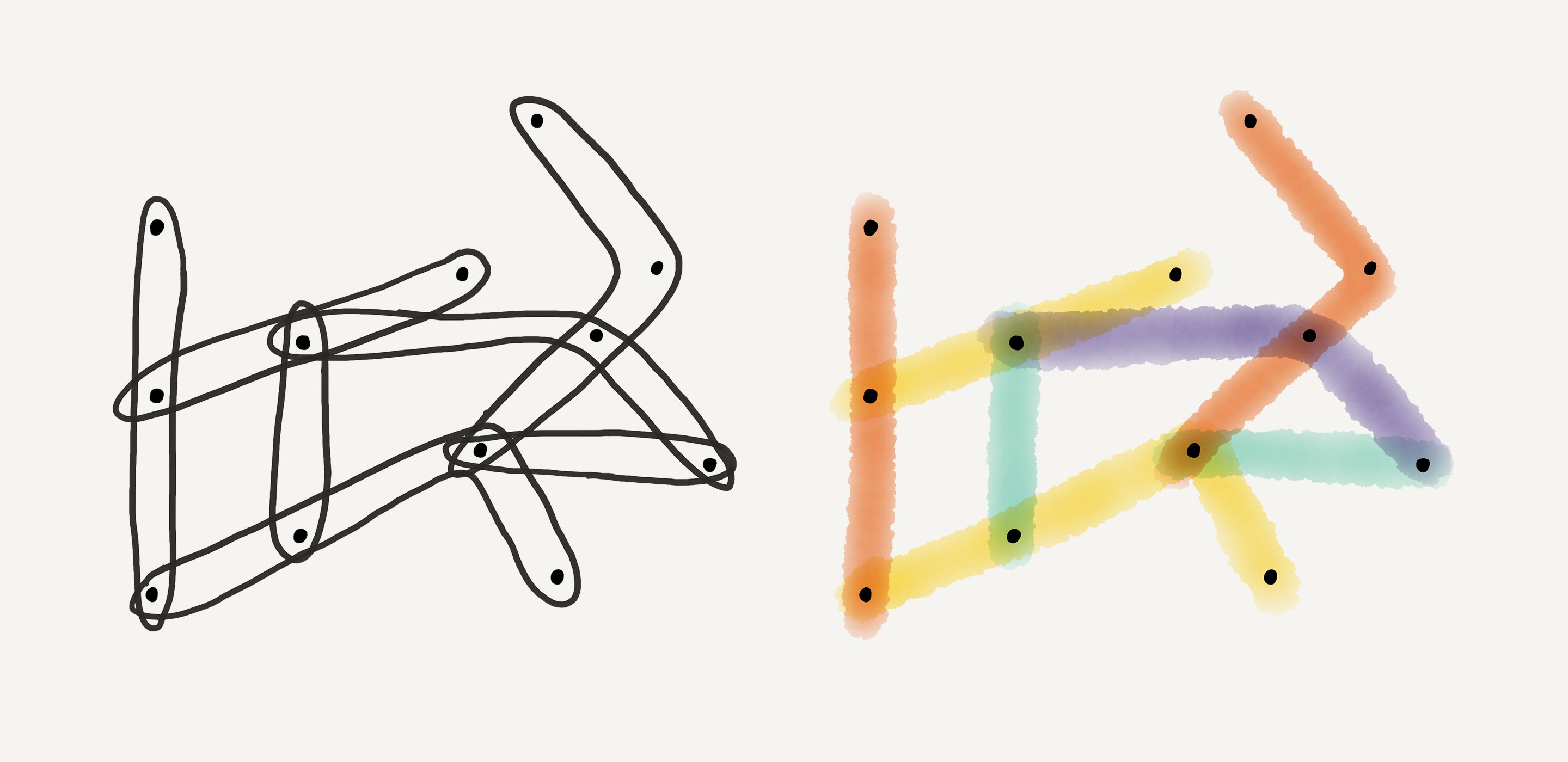
The Erdős-Faber-Lovász conjecture is a coloring question about a specific type of hypergraph where the edges overlap minimally. In these structures, known as linear hypergraphs, no two edges are allowed to overlap at more than one vertex. The conjecture predicts that the chromatic index of a linear hypergraph is never more than its number of vertices. In other words, if a linear hypergraph has nine vertices, its edges can be colored with no more than nine colors, regardless of how you draw them.
The extreme generality of the Erdős-Faber-Lovász conjecture makes it challenging to prove. As you move to hypergraphs with more and more vertices, the ways of arranging their looping edges multiply as well. With all these possibilities, it might seem likely that there is some configuration of edges that requires more colors than it has vertices.
“There are so many different types of hypergraphs that have completely different flavors,” said Abhishek Methuku, one of the authors of the new proof, along with Dong-yeap Kang, Tom Kelly, Daniela Kühn and Deryk Osthus, all of the University of Birmingham. “It is surprising that it is true.”
Proving this surprising prediction meant confronting several types of hypergraphs that are particularly challenging to color — and establishing that there are no other examples that are even harder.
Three Extreme Hypergraphs
If you’re doodling on a page and you draw a linear hypergraph, its chromatic index will probably be far less than its number of vertices. But there are three types of extreme hypergraphs that push the limit.
In the first one, each edge connects just two vertices. It’s usually called a complete graph, because every pair of vertices is connected by an edge. Complete graphs with an odd number of vertices have the maximum chromatic index allowed by the Erdős-Faber-Lovász conjecture.
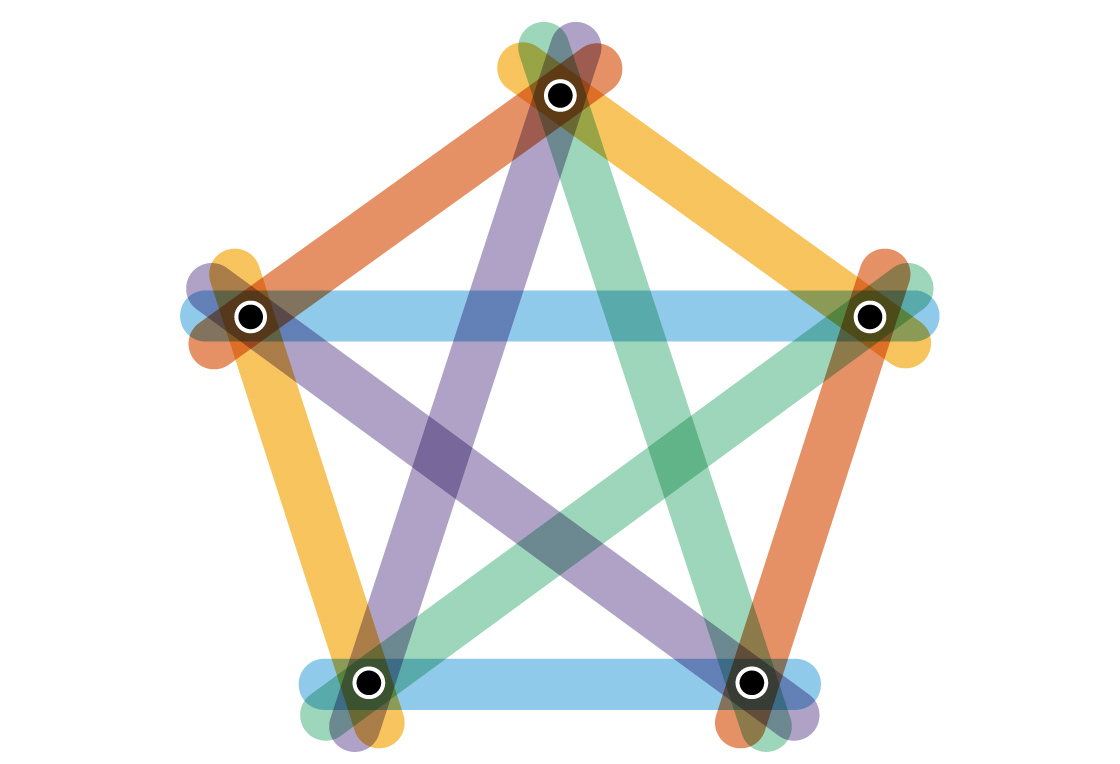
Samuel Velasco/Quanta Magazine
The second extreme example is, in a sense, the opposite of a complete graph. Where edges in a complete graph only connect a small number of vertices (two), all edges in this type of graph connect a large number of vertices (as the number of total vertices grows, so does the number encompassed by each edge). It is called the finite projective plane, and, like the complete graph, it has the maximum chromatic index.
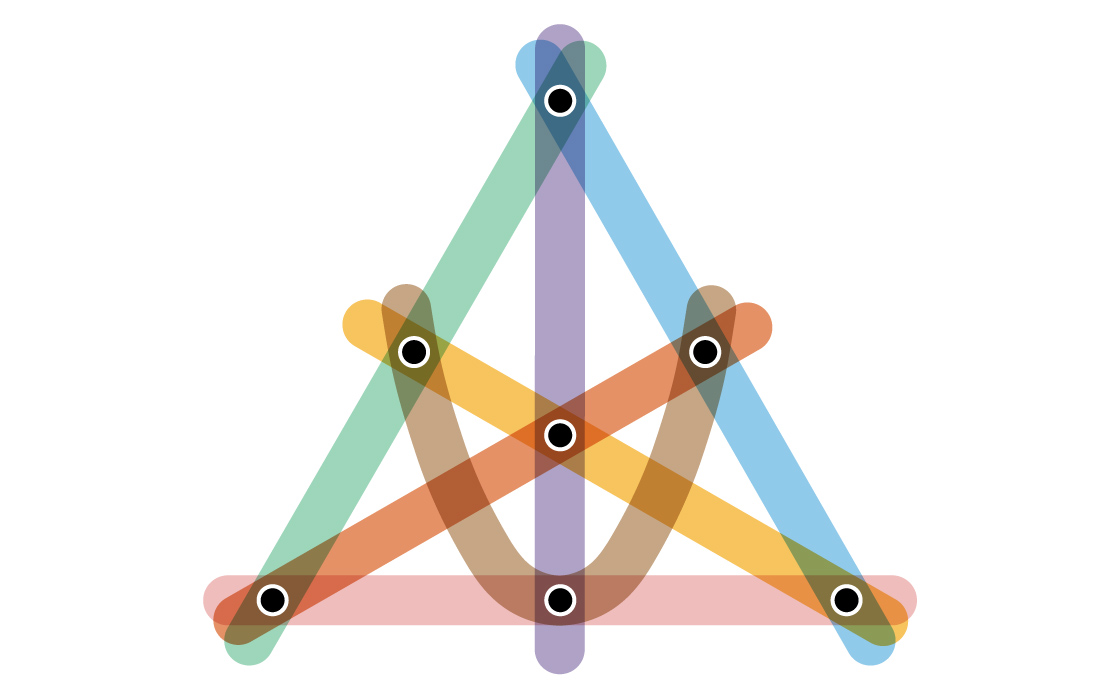
The third extreme falls in the middle of the spectrum — with small edges that join just two vertices and large edges that join many vertices. In this type of graph you often have one special vertex connected to each of the others by lone edges, then a single large edge that scoops up all the others.
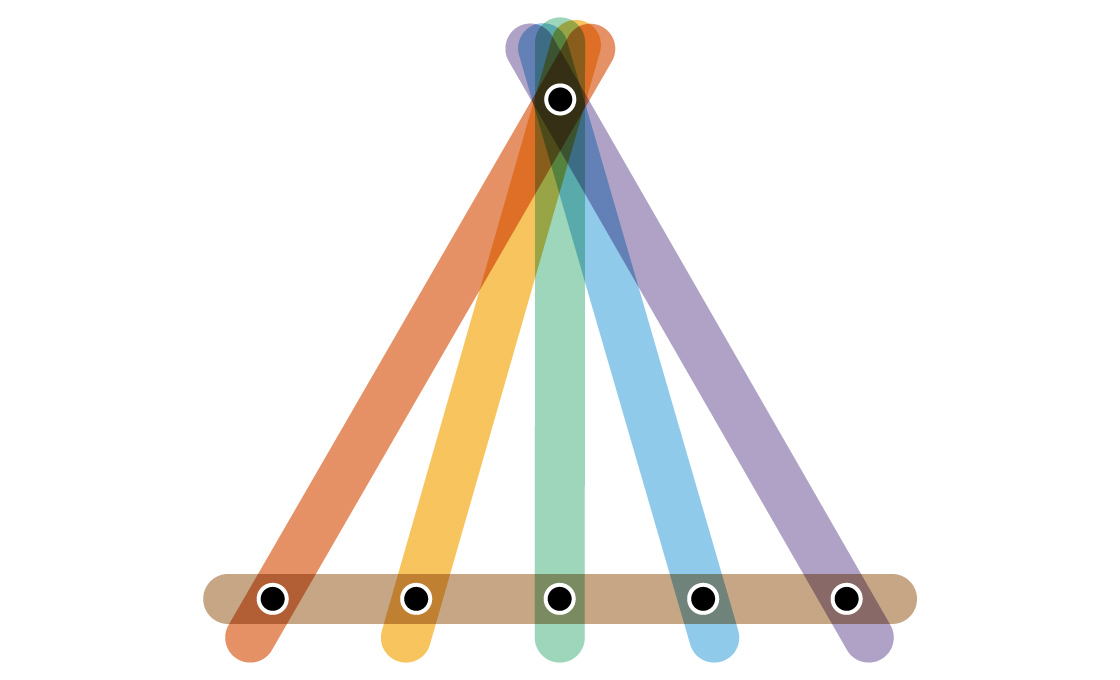
If you slightly modify one of the three extreme hypergraphs, the result will typically also have the maximum chromatic index. So each of the three examples represents a broader family of challenging hypergraphs, which for years have held back mathematicians’ efforts to prove the Erdős-Faber-Lovász conjecture.
When a mathematician first encounters the conjecture, they may attempt to prove it by generating a simple algorithm or an easy procedure that specifies a color to assign to each edge. Such an algorithm would need to work for all hypergraphs and only use as many colors as there are vertices.
But the three families of extreme hypergraphs have very different shapes. So any technique for proving that it’s possible to color one of the families typically fails for hypergraphs in the other two families.
“It is quite difficult to have a common theorem to incorporate all the extremal cases,” said Kang.
While Erdős, Faber and Lovász knew about these three extreme hypergraphs, they didn’t know if there were any others that also have the maximum chromatic index. The new proof takes this next step. It demonstrates that any hypergraph that is significantly different from these three examples requires fewer colors than its number of vertices. In other words, it establishes that hypergraphs that resemble these three are as tough as it gets.
“If you exclude these three families, we kind of show that there are not more bad examples,” said Osthus. “If you’re not too close to any of these, then you can use significantly less colors.”
Sorting Edges
The new proof builds on progress by Jeff Kahn of Rutgers University who proved an approximate version of the Erdős-Faber-Lovász conjecture in 1992. Last November, Kühn and Osthus (both senior mathematicians) and their team of three postdocs — Kang, Kelly and Methuku — set out to improve Kahn’s result, even if they didn’t solve the full conjecture.
But their ideas were more powerful than they expected. As they set to work, they started to realize that they might be able to prove the conjecture exactly.
“It was all kind of magic,” said Osthus. “It was very lucky that somehow the team we had fit it exactly.”
They started by sorting the edges of a given hypergraph into several different categories based on edge size (the number of vertices an edge connects).
After this sorting they turned to the hardest-to-color edges first: edges with many vertices. Their strategy for coloring the large edges relied on a simplification. They reconfigured these edges as the vertices of an ordinary graph (where each edge only connects two vertices). They colored them using established results from standard graph theory and then transported that coloring back to the original hypergraph.
“They’re pulling in all kinds of stuff that they and other people have been developing over decades,” said Kahn.
After coloring the largest edges, they worked their way downward, saving the smallest edges of a graph for last. Since small edges touch fewer vertices, they’re easier to color. But saving them for last also makes the coloring harder in one way: By the time the authors got to the small edges, many of the available colors had already been used on other adjacent edges.
To address this, the authors took advantage of a new technique in combinatorics called absorption that they and others have been using recently to settle a range of questions.
“Daniela and Deryk have a lot of results looking at other famous questions using it. Now their group managed to prove the [Erdős-Faber-Lovász] theorem using this method,” said Kalai.
Absorbing Colors
The authors use absorption as a way of gradually adding edges into a coloring while ensuring along the way that the coloring always maintains the right properties. It’s especially useful for coloring the places where many small edges converge on a single vertex, like the special vertex connected to all the others in the third extreme hypergraph. Clusters like these use almost all the available colors and need to be colored carefully.
To do so, the authors created a reservoir of small edges, pulled from these tricky clusters. Then they applied a random coloring procedure to many of the small edges that remained (basically, rolling a die to decide which color to apply to a given edge). As the coloring proceeded, the authors strategically chose from the unused colors and applied them in a carefully chosen way to the reserved edges, “absorbing” them into the colorings.
Absorption improves the efficiency of the random coloring procedure. Coloring edges randomly is a nice basis for a very general procedure, but it’s also wasteful — if applied to all edges, it’s unlikely to produce the optimal configuration of colors. But the recent proof tempers the flexibility of random colorings by complementing it with absorption, which is a more exact method.
In the end — having colored the largest edges of a graph with one technique and then the smaller edges using absorption and other methods — the authors were able to prove that the number of colors required to color the edges of any linear hypergraph is never more than the number of vertices. This proves that the Erdős-Faber-Lovász conjecture is true.
Because of the probabilistic elements, their proof only works for large enough hypergraphs — those with more than a specific number of vertices. This approach is common in combinatorics, and mathematicians consider it a nearly complete proof since it only omits a finite number of hypergraphs.
“There is still the assumption in the paper that the number of nodes must be very large, but that’s probably just some additional work,” said Lovász. “Essentially, the conjecture is now proved.”
The Erdős-Faber-Lovász conjecture started as a question that seemed as if it could be asked and answered within the span of a single party. In the years that followed, mathematicians realized the conjecture was not as simple as it sounded, which is maybe what the three mathematicians would have wanted anyway. One of the only things better than solving a math problem over tea is coming up with one that ends up inspiring decades of mathematical innovation on the way to its final resolution.
“Efforts to prove it forced the discovery of techniques that have more general application,” said Kahn. “This is kind of the way Erdős got at mathematics.”
This article was reprinted on Wired.com.



