When Math Gets Impossibly Hard

James O’Brien for Quanta Magazine
Introduction
We like to say that anything is possible. In Norton Juster’s novel The Phantom Tollbooth, the king refuses to tell Milo that his quest is impossible because “so many things are possible just as long as you don’t know they’re impossible.” In reality, however, some things are impossible, and we can use mathematics to prove it.
People use the term “impossible” in a variety of ways. It can describe things that are merely improbable, like finding identical decks of shuffled cards. It can describe tasks that are practically impossible due to a lack of time, space or resources, such as copying all the books in the Library of Congress in longhand. Devices like perpetual-motion machines are physically impossible because their existence would contradict our understanding of physics.
Mathematical impossibility is different. We begin with unambiguous assumptions and use mathematical reasoning and logic to conclude that some outcome is impossible. No amount of luck, persistence, time or skill will make the task possible. The history of mathematics is rich in proofs of impossibility. Many are among the most celebrated results in mathematics. But it was not always so.
The punishment for what was perhaps the first proof of impossibility was severe. Historians believe that in the fifth century BCE, Hippasus of Metapontum, a follower of the cult leader Pythagoras, discovered that it is impossible to find a line segment that can be placed end-to-end to measure both the side and the diagonal of a regular pentagon. Today we say that the length of a diagonal of a regular pentagon with side length 1 — the golden ratio, $latex \phi$ = $latex \frac{1}{2}$ (1 + $latex \sqrt{5}$) — is “irrational.” Hippasus’ discovery flew in the face of the Pythagorean credo that “all is number,” so, according to legend, he was either drowned at sea or banished from the Pythagoreans.
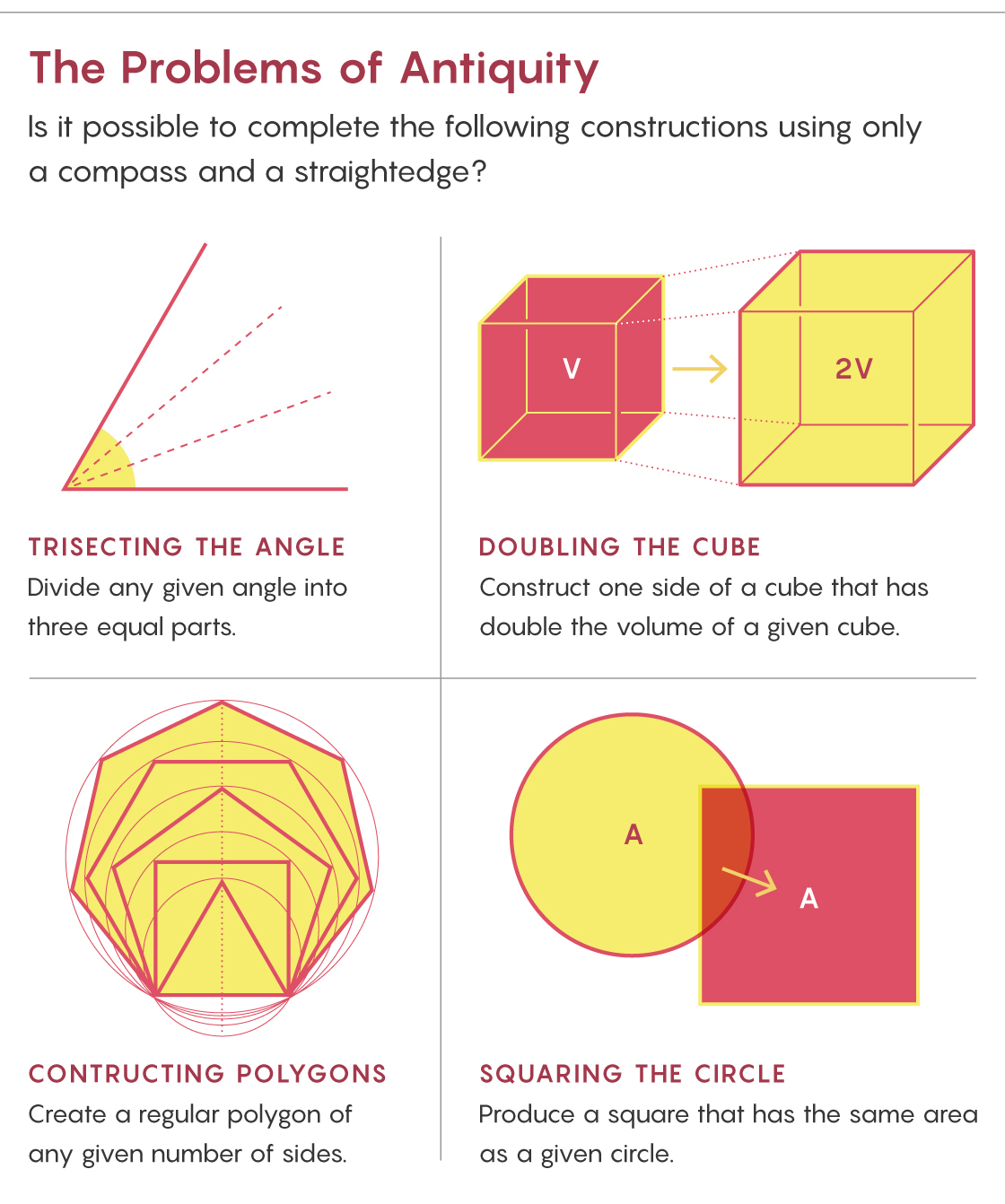
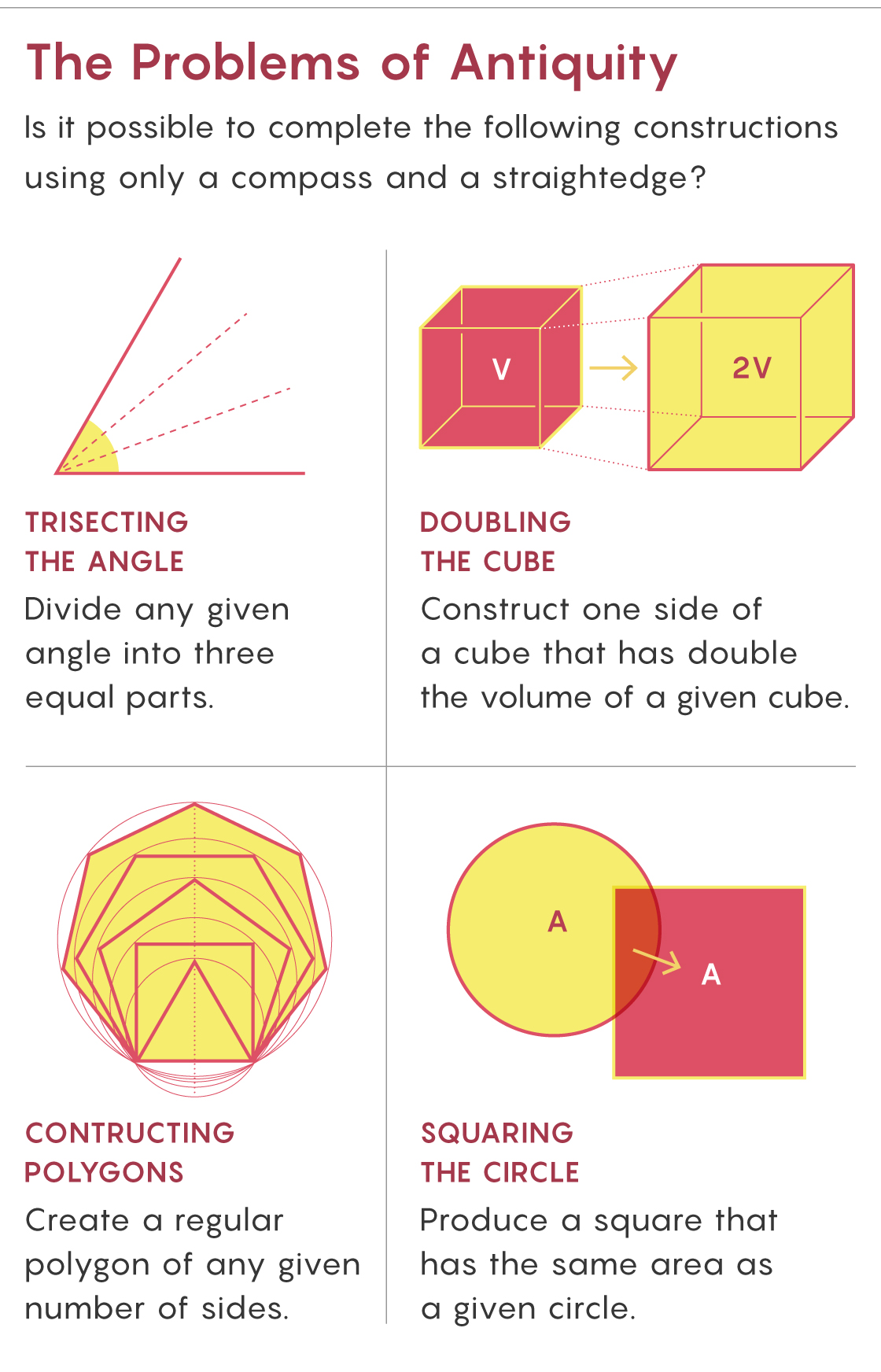
More than a century later, Euclid elevated the line and the circle, considering them the fundamental curves in geometry. Thereafter, generations of geometers performed constructions — bisecting angles, drawing perpendicular bisectors, and so on — using only a compass and a straightedge. But certain seemingly simple constructions stymied the Greek geometers, eventually taking on a mythical status and vexing mathematicians for over 2,000 years: trisecting any given angle, producing the side of a cube with twice the volume of a given one, creating every regular polygon, and constructing a square with the same area as a given circle.
Samuel Velasco/Quanta Magazine
Although these problems are geometric in nature, the proofs of their impossibility are not. To show that they cannot be solved required new mathematics.
In the 17th century, René Descartes made a fundamental discovery: Assuming we restrict ourselves to the compass and straightedge, it’s impossible to construct segments of every length. If we begin with a segment of length 1, say, we can only construct a segment of another length if it can be expressed using the integers, addition, subtraction, multiplication, division and square roots (as the golden ratio can).
Thus, one strategy to prove that a geometric problem is impossible — that is, not constructible — is to show that the length of some segment in the final figure cannot be written in this way. But doing so rigorously required the nascent field of algebra.
Two centuries later, Descartes’ countryman Pierre Wantzel used polynomials (the sums of coefficients and variables raised to powers) and their roots (values that make the polynomials equal zero) to attack these classical problems. In the cube doubling problem, for example, the side length of a cube with twice the volume of the unit cube is $latex \sqrt[3]{2}$, which is a root of the polynomial x³ − 2 because ($latex \sqrt[3]{2}$)³ − 2 = 0.
In 1837, Wantzel proved that if a number is constructible, it must be a root of a polynomial that cannot be factored and whose degree (the largest power of x) is a power of 2. For instance, the golden ratio is a root of the degree-two polynomial x² − x − 1. But x³ − 2 is a degree-three polynomial, so ($latex \sqrt[3]{2}$) is not constructible. Thus, Wantzel concluded, it is impossible to double the cube.
In a similar way, he proved that it is impossible to use the classical tools to trisect every angle or to construct certain regular polygons, such as one with seven sides. Remarkably, all three impossibility proofs appeared on the same page. Just as Isaac Newton and Albert Einstein each had their annus mirabilis, or miraculous years, perhaps we should call this the pagina mirabilis — the miraculous page.
Proving the impossibility of the remaining problem, squaring the circle, required something new. In 1882, Ferdinand von Lindemann proved the key result — that π is not constructible — by proving it is transcendental; that is, π isn’t the root of any polynomial.
These classical problems could go down in infamy as sirens whose songs lured mathematicians to crash on the rocky shores of impossibility. But I see them as muses who inspired generations of creative thinkers.
The same holds true for a more recent impossible problem, which arises from the simple act of crossing a bridge. Imagine you live in Pittsburgh, the “city of bridges,” as many of my students do. An adventurous bicyclist might wonder if it is possible to start from home, ride exactly once across each of the 22 bridges spanning Pittsburgh’s major rivers, and end up back home.
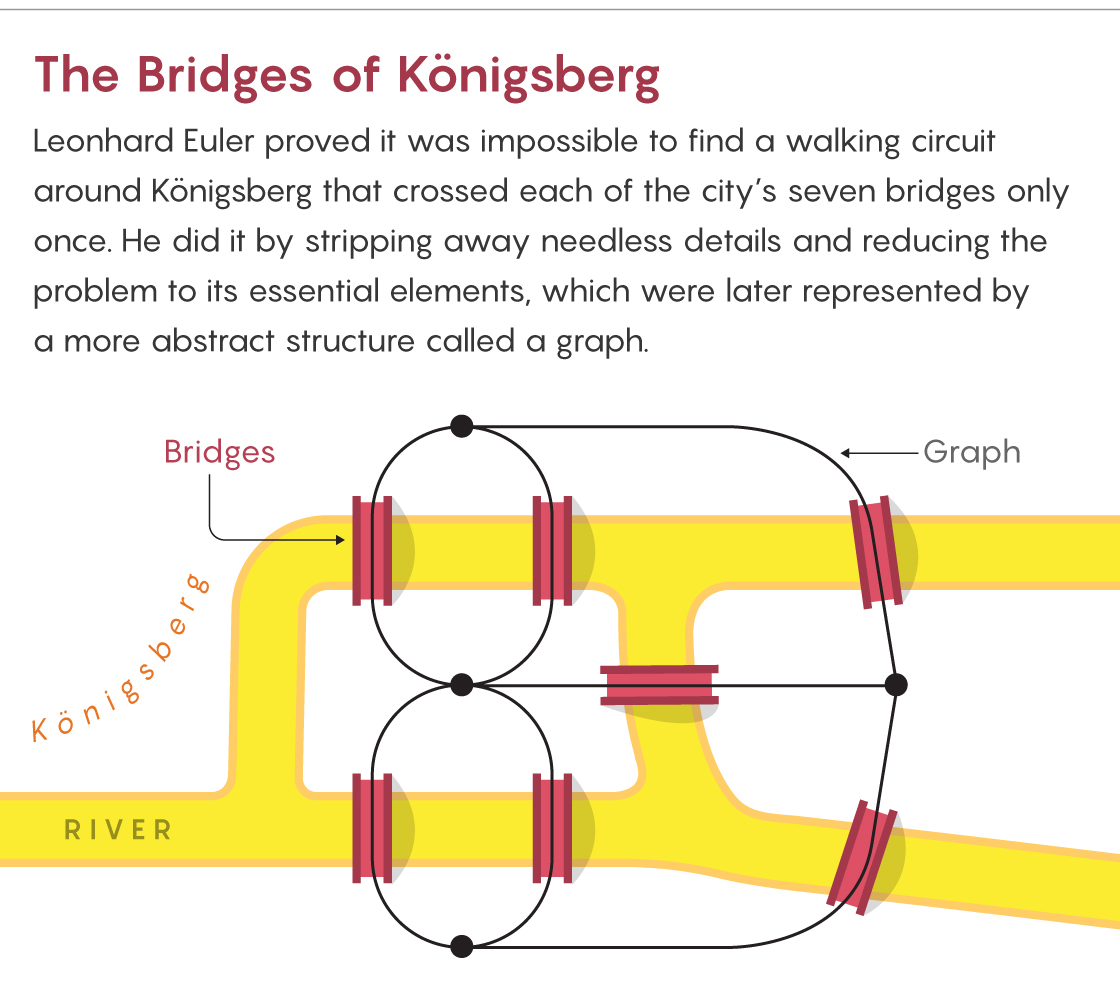
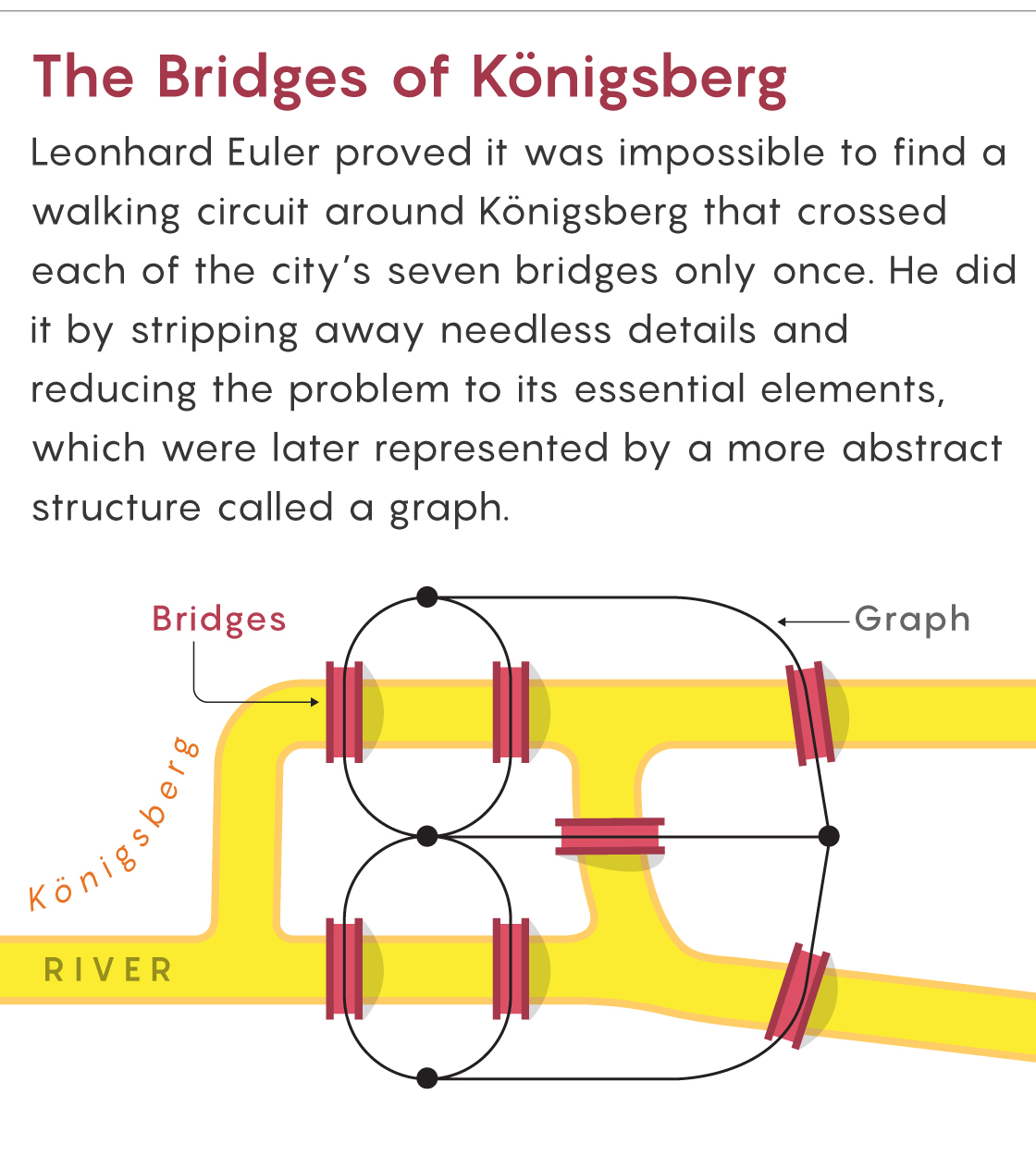
In 1735, a Prussian mayor posed the same problem to Leonhard Euler about Königsberg (now Kaliningrad), a city with seven bridges joining three riverbanks and an island. At first, Euler dismissed the problem as nonmathematical: “This type of solution bears little relationship to mathematics, and I do not understand why you expect a mathematician to produce it, rather than anyone else.”
Yet Euler soon proved it was impossible, and in so doing he created a field he called the geometry of position, which we now call topology. He recognized that the exact details — the precise locations of the bridges, the shapes of the landmasses, and so on — were unimportant. All that mattered were the connections. Later mathematicians streamlined Euler’s arguments using what we now call graphs or networks. This idea of connectedness is central to the study of social networks, the internet, epidemiology, linguistics, optimal route planning and more.
Samuel Velasco/Quanta Magazine
Euler’s proof is surprisingly simple. He reasoned that each time we enter and leave a region, we must cross two bridges. So every landmass must have an even number of bridges. Because every landmass in Königsberg had an odd number of bridges, no such round trip was possible. Likewise, the three bridges to Herrs Island in the Allegheny River make a bicycle circuit of Pittsburgh mathematically impossible.
As this problem demonstrates, impossibility results are not confined to the realm of abstract mathematics. They can have real-world implications — sometimes even political ones.
Recently, mathematicians have turned their attention to gerrymandering. In the United States, after every census, states must redraw their congressional districts, but sometimes the ruling party divides the state into ridiculous shapes to maximize its own seats and thus its political power.
Many states require that districts be “compact,” a term with no fixed mathematical definition. In 1991, Daniel Polsby and Robert Popper proposed 4πA/P² as a way to measure the compactness of a district with area A and perimeter P. Values range from 1, for a circular district, to close to zero, for misshapen districts with long perimeters.
Meanwhile, Nicholas Stephanopoulos and Eric McGhee introduced the “efficiency gap” in 2014 as a measure of the political fairness of a redistricting plan. Two gerrymandering strategies are to ensure that the opposition party stays below the 50% threshold in districts (called cracking), or near the 100% level (stacking). Either tactic forces the other party to waste votes on losing candidates or on winning candidates who don’t need the votes. The efficiency gap captures the relative numbers of wasted votes.
These are both useful measures for detecting gerrymandering. But in 2018, Boris Alexeev and Dustin Mixon proved that “sometimes, a small efficiency gap is only possible with bizarrely shaped districts.” That is, it is mathematically impossible to always draw districts that meet certain Polsby-Popper and efficiency-gap fairness targets.
But finding methods to detect and prevent partisan gerrymandering is an active scholarly area that’s attracting many talented researchers. As with the problems of antiquity and the Königsberg bridge problem, I’m sure the gerrymandering problem will inspire creativity and push mathematics forward.



