What's up in
Combinatorics
Latest Articles
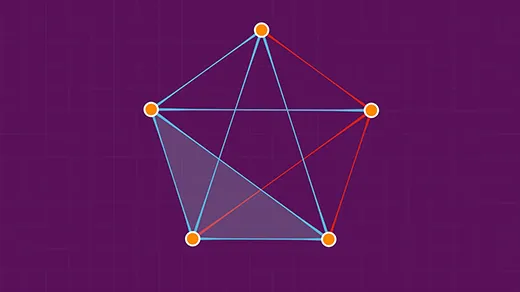
Mathematicians Discover Novel Way to Predict Structure in Graphs
Mathematicians probe the limits of randomness in new work estimating quantities called Ramsey numbers.
First-Year Graduate Student Finds Paradoxical Set
No two pairs have the same sum; add three numbers together, and you can get any whole number.
How Math Has Changed the Shape of Gerrymandering
New tools make it possible to detect hidden manipulation of maps.
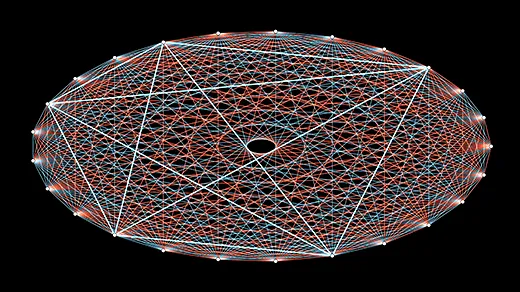
A Very Big Small Leap Forward in Graph Theory
Four mathematicians have found a new upper limit to the “Ramsey number,” a crucial property describing unavoidable structure in graphs.
Why Mathematicians Re-Prove What They Already Know
It’s been known for thousands of years that the primes go on forever, but new proofs give fresh insights into how theorems depend on one another.
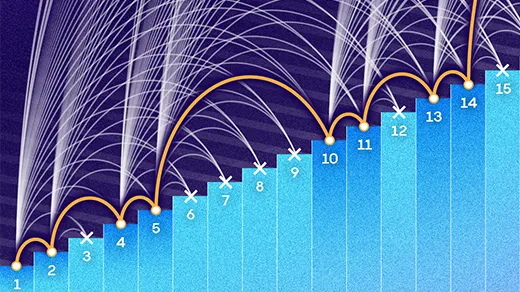
The Number 15 Describes the Secret Limit of an Infinite Grid
The “packing coloring” problem asks how many numbers are needed to fill an infinite grid so that identical numbers never get too close to one another. A new computer-assisted proof finds a surprisingly straightforward answer.
Mathematicians Find Hidden Structure in a Common Type of Space
In 50 years of searching, mathematicians found only one example of a “subspace design” in a vector space. A new proof reveals that there are infinitely more out there.
Surprise Computer Science Proof Stuns Mathematicians
For decades, mathematicians have been inching forward on a problem about which sets contain evenly spaced patterns of three numbers. Last month, two computer scientists blew past all of those results.
Coloring by Numbers Reveals Arithmetic Patterns in Fractions
In a recent paper, two mathematicians showed that a particular pattern is unavoidable when fractions are categorized.