What's up in
Combinatorics
Latest Articles
Why Mathematicians Re-Prove What They Already Know
It’s been known for thousands of years that the primes go on forever, but new proofs give fresh insights into how theorems depend on one another.
The Number 15 Describes the Secret Limit of an Infinite Grid
The “packing coloring” problem asks how many numbers are needed to fill an infinite grid so that identical numbers never get too close to one another. A new computer-assisted proof finds a surprisingly straightforward answer.
Mathematicians Find Hidden Structure in a Common Type of Space
In 50 years of searching, mathematicians found only one example of a “subspace design” in a vector space. A new proof reveals that there are infinitely more out there.
Surprise Computer Science Proof Stuns Mathematicians
For decades, mathematicians have been inching forward on a problem about which sets contain evenly spaced patterns of three numbers. Last month, two computer scientists blew past all of those results.
Coloring by Numbers Reveals Arithmetic Patterns in Fractions
In a recent paper, two mathematicians showed that a particular pattern is unavoidable when fractions are categorized.
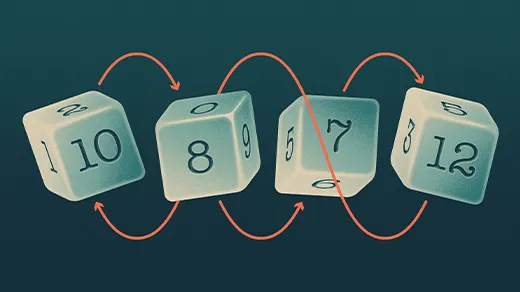
Mathematicians Roll Dice and Get Rock-Paper-Scissors
Mathematicians have uncovered a surprising wealth of rock-paper-scissors-like patterns in randomly chosen dice.
Google Researcher, Long Out of Math, Cracks Devilish Problem About Sets
On nights and weekends, Justin Gilmer attacked an old question in pure math using the tools of information theory.
The Year in Math
Four Fields Medals were awarded for major breakthroughs in geometry, combinatorics, statistical physics and number theory, even as mathematicians continued to wrestle with how computers are changing the discipline.
From Systems in Motion, Infinite Patterns Appear
Mathematicians are finding inevitable structures in sufficiently large sets of integers.