What's up in
Ramsey theory
Latest Articles
Math’s ‘Oldest Problem Ever’ Gets a New Answer
A new proof significantly strengthens a decades-old result about the ubiquity of ways to represent whole numbers as sums of unit fractions.
Mathematician Hurls Structure and Disorder Into Century-Old Problem
A new paper shows how to create longer disordered strings than mathematicians had thought possible, proving that a well-known recent conjecture is “spectacularly wrong.”
New Proof Reveals That Graphs With No Pentagons Are Fundamentally Different
Researchers have proved a special case of the Erdős-Hajnal conjecture, which shows what happens in graphs that exclude anything resembling a pentagon.
Undergraduate Math Student Pushes Frontier of Graph Theory
At 21, Ashwin Sah has produced a body of work that senior mathematicians say is nearly unprecedented for a college student.
Disorder Persists in Larger Graphs, New Math Proof Finds
David Conlon and Asaf Ferber have raised the lower bound for multicolor “Ramsey numbers,” which quantify how big graphs can get before patterns inevitably emerge.
‘Rainbows’ Are a Mathematician’s Best Friend
“Rainbow colorings” recently led to a new proof. It’s not the first time they’ve come in handy.
Rainbow Proof Shows Graphs Have Uniform Parts
Mathematicians have proved that copies of smaller graphs can always be used to perfectly cover larger ones.
Mathematicians Catch a Pattern by Figuring Out How to Avoid It
We finally know how big a set of numbers can get before it has to contain a pattern known as a “polynomial progression.”
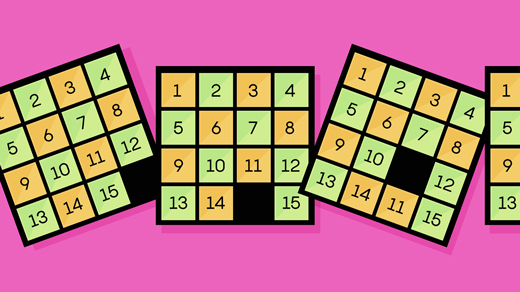
Mathematicians Calculate How Randomness Creeps In
Mathematicians have figured out exactly how many moves it takes to randomize a 15 puzzle.