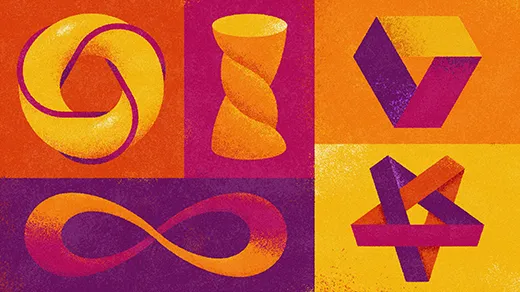What's up in
Topology
Latest Articles
Monumental Proof Settles Geometric Langlands Conjecture
In work that has been 30 years in the making, mathematicians have proved a major part of a profound mathematical vision called the Langlands program.
How Failure Has Made Mathematics Stronger
The topologist Danny Calegari discusses the inevitability of disappointment in math, and how to learn from it.
Strangely Curved Shapes Break 50-Year-Old Geometry Conjecture
Mathematicians have disproved a major conjecture about the relationship between curvature and shape.
Mathematicians Marvel at ‘Crazy’ Cuts Through Four Dimensions
Topologists prove two new results that bring some order to the confoundingly difficult study of four-dimensional shapes.
Topologists Tackle the Trouble With Poll Placement
Mathematicians are using topological abstractions to find places where it’s hard to vote.
A New Agenda for Low-Dimensional Topology
This past October, dozens of mathematicians gathered in Pasadena to create the third version of “Kirby’s list” — a compendium of the most important unsolved problems in the field.
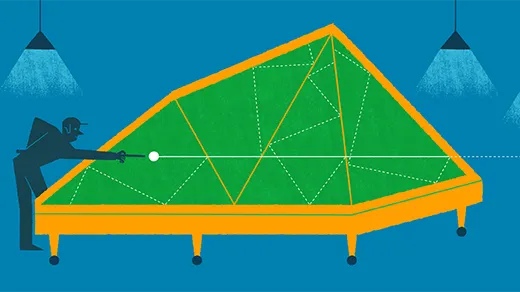
Unfolding the Mysteries of Polygonal Billiards
The surprisingly subtle geometry of a familiar game shows how quickly math gets complicated.
What Makes for ‘Good’ Mathematics?
Terence Tao, who has been called the “Mozart of Mathematics,” wrote an essay in 2007 about the common ingredients in “good” mathematical research. In this episode, the Fields Medalist joins Steven Strogatz to revisit the topic.
Mathematicians Identify the Best Versions of Iconic Shapes
Researchers are discovering the shortest knots and fattest Möbius strips, among other “optimal shapes.”