What's up in
Probability
Latest Articles
A Close-Up View Reveals the ‘Melting’ Point of an Infinite Graph
Just as ice melts to water, graphs undergo phase transitions. Two mathematicians showed that they can pinpoint such transitions by examining only local structure.
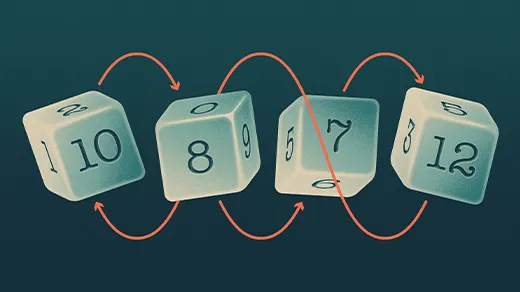
Mathematicians Roll Dice and Get Rock-Paper-Scissors
Mathematicians have uncovered a surprising wealth of rock-paper-scissors-like patterns in randomly chosen dice.
Probability and Number Theory Collide — in a Moment
Mathematicians are taking ideas developed to study random numbers and applying them to a broad range of categories.
How Do Mathematicians Know Their Proofs Are Correct?
What makes a proof stronger than a guess? What does evidence look like in the realm of mathematical abstraction? Hear the mathematician Melanie Matchett Wood explain how probability helps to guide number theorists toward certainty.
Elegant Six-Page Proof Reveals the Emergence of Random Structure
Two young mathematicians have astonished their colleagues with a full proof of the Kahn-Kalai conjecture — a sweeping statement about how structure emerges in random sets and graphs.
Neural Noise Shows the Uncertainty of Our Memories
The electrical chatter of our working memories reflects our uncertainty about their contents.
Mathematicians Answer Old Question About Odd Graphs
A pair of mathematicians solved a legendary question about the proportion of vertices in a graph with an odd number of connections.
Mathematicians Settle Erdős Coloring Conjecture
Fifty years ago, Paul Erdős and two other mathematicians came up with a graph theory problem that they thought they might solve on the spot. A team of mathematicians has finally settled it.
How Neutral Theory Altered Ideas About Biodiversity
The simple insight that most changes are random had a profound effect on genetics, evolution and ecology.